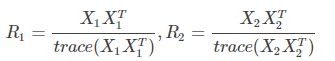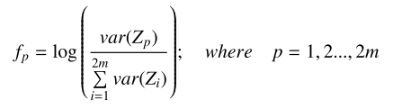matlab csp共空间代码,运动想象中共空间模式算法（CSP）的实现

最近在研究运动想象算法，其中CSP来提取特征用的比较多，尤为是在二分类的问题中，以前写过一篇如何在MNE库中实现CSP算法的博客，用的是MNE库中已经写好的算法，如今想本身实现该算法，研究了几天发现坑仍是比较多的。。。先列出一些参考的博客文章，里面有对应的算法在matlab中的实现，后面主要是解释算法中的一些细节以及本身对该算法的理解。强烈建议下载本博客的资源包对照着看，里面是整理好的博客中用到的资料。html

CSP原理：算法

CSP在Python MNE库中的实现编程

matlab代码实现：函数

上面既然都有实现好的版本了，本着拿来主义的思想原本不打算本身开发的，可是考虑到后面须要支持多种编程语言的实现，以及验证算法的准确性，我在python中也实现了一遍，并尝试理解每一条语句的意义，及其对应的原理。不弄不知道啊，一弄发现了不少有趣的细节。3d

一句话总结CSP算法：共空间模式算法的基本原理是利用矩阵的对角化。找到一组最优空间滤波器进行投影，使两类信号的方差差别化最大，从而获得具备较高区分度的特征向量。

上面所说的特征向量也就至关于滤波器，输入数据通过和特征向量的运算就会获得最大差别化方差的信号，这个信号我理解为是“原始波形”，测量结果=原始波形 * 电极位置，这一点在后面会详细解释。

算法的实现原理在前面的博客中都有所介绍，但愿你们能对照着看，公式的推导这里就再也不赘述，下面主要说一下对应的代码实现中遇到的问题。

问题1 求协方差矩阵

全部的资料第一步都是求对应数据的协方差矩阵，其对应的计算公式为

不知道你们有没有注意到这根本不是协方差矩阵的标准形式，协方差矩阵的计算方法见：https://blog.csdn.net/Mr_HHH/article/details/78490576。协方差的计算应该是去均值后的数据，而且是对列的运算，矩阵X的协方差计算公式为：

那为何在这里会这么计算呢？对行计算这个问题好解释，由于脑波数据通常都是按行存储的，这就是转置的问题。但是为何它不用减去均值，而且也没有求平均。这个问题困扰了我很久，最后在一篇文献中找到了想要的答案。

《Designing optimal spatial filters for single-trial EEG classification in a movement task》文章的796页有以下两段话。

第一段话主要的意思是说，EEG数据是滤波后的，均值为零，看到这恍然大悟，滤波后的数据没有直频份量，均值那可不就是零么，那也就不用减均值了。

第二段话主要的意思是说，正则化是为了消除不一样实验对值的影响，因此使用的是迹。

问题2 特征值排序获取白化矩阵

排序是为了找到影响大的特征向量这个好理解，在文章《Multiclass Common Spatial Pattern for EEG based Brain Computer Interface with Adaptive Learning Classifier》中第3页有提到这个步骤。

上文提到的matlab代码中有一个小问题，代码中直接对特征值进行了排序，我我的的理解是应该对特征值的绝对值排序，由于特征值有可能出现负值的。

问题3 为何最后提取的特征值是和方差有关的一个量

提取特征的计算公式以下，可为何是方差呢?

这个问题在《Optimizing spatial filters for robust EEG single-trial analysis》一文中有所解释，文章的第4页有以下一段话，大体的意思是说带通滤波后的信号方差和能量有关，虽然仍是不太理解，不过总算找到一些理论依据了。

在上面提到的matlab代码中，在提取特征的时候，还对方差求了一个log:

我想做者多是借鉴了《Multiclass Common Spatial Pattern for EEG based Brain Computer Interface with Adaptive Learning Classifier》这篇文章，文章第3页中有以下公式：

matlab代码的Python实现

至此流程上算是理解了，参考matlab中的实现，实现了该算法的python版，为了对比计算结果，保留了特征值排序的问题，至关于matlab代码中一比一的实现。

EEG_Channels = trainData.shape[1]

EEG_Trials = trainData.shape[0]

classLabels = np.unique(trainLabels)

EEG_Classes = len(classLabels)

covMatrix = list(range(EEG_Classes))

trialCov = np.zeros([EEG_Channels, EEG_Channels, EEG_Trials])

for i in range(EEG_Trials):

E = trainData[i]

EE = np.dot(E, E.T)

trialCov[:, :, i] = EE/np.trace(EE)

for i in range(EEG_Classes):

covMatrix[i] = np.mean(trialCov[:, :, trainLabels == classLabels[i]], 2)

print('a' ,covMatrix[0])

print(covMatrix[1])

covTotal = covMatrix[0] + covMatrix[1]

#########特征值降序

eigenvalues, featurevectors = np.linalg.eig(covTotal)

egIndex = np.argsort(eigenvalues)[::-1]

eigenvalues = np.sort(eigenvalues)[::-1]

Ut = featurevectors[:, egIndex]

# 矩阵白化

P = np.dot(np.diag(np.sqrt(1/eigenvalues)), Ut.T)

# 矩阵P做用求公共特征向量transformedCov1

transformedCov1 = P.dot(covMatrix[0]).dot(P.T)

# 计算公共特征向量transformedCov1的特征向量和特征矩阵

eigenvalues, featurevectors = np.linalg.eig(transformedCov1)

egIndex = np.argsort(eigenvalues)[::-1]

eigenvalues = np.sort(eigenvalues)[::-1]

U1 = featurevectors[:, egIndex]

# 计算投影矩阵W

CSPMatrix = U1.T.dot(P)

# 计算特征矩阵

FilterPairs = 2

feature_train = np.zeros([EEG_Trials, 2*FilterPairs+1])

feature_test = np.zeros([EEG_Trials, 2*FilterPairs+1])

Filter = np.r_[CSPMatrix[:FilterPairs], CSPMatrix[-FilterPairs:]]

#从每一次实验中提取CSP特征

for t in range(EEG_Trials):

# 将数据投影到CSP空间

projectedTrial_train = Filter.dot(trainData[t])

projectedTrial_test = Filter.dot(trainData[t])

# 投影后信号的方差做为特征

variances_train = np.var(projectedTrial_train, 1)

variances_test = np.var(projectedTrial_test, 1)

for f in range(len(variances_train)):

feature_train[t, f] = np.log(variances_train[f])

for f in range(len(variances_test)):

feature_test[t, f] = np.log(variances_test[f])

CSP_Train_faetures = feature_train[:, 0:4]

CSP_Test_features = feature_test[:, 0:4]

与Python中MNE库的对比

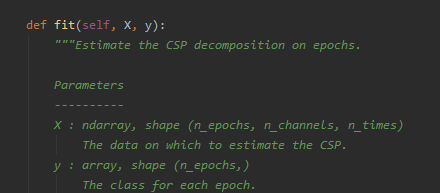
到目前为止算法算是已经实现了，但是这么作对不对呢，MNE库中有写好的CSP算法，对比一下看看结果。不比不知道啊，一比呵呵了，结果彻底不同啊，只好查看MNE库的源码看看了。主要的计算流程在csp.py中的fit函数中，这里截取其中的部分代码进行解释说明。

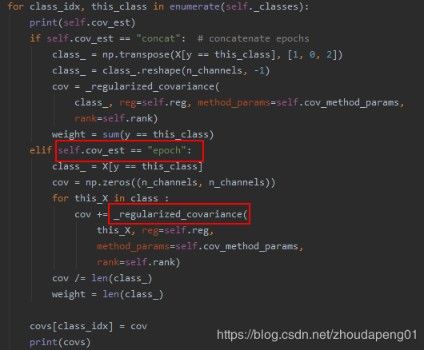
在MNE库中第一步也是求协方差矩阵，这里有两种计算方式“concact”和“epoch”，concact是拼接后再求方差。

对应上面的程序，至关于使用的是epoch方法，

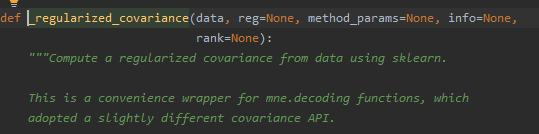
但是这个协方差的计算看起来也很诡异啊，_regularized_covariance是什么鬼，python中有cov函数啊，但是为何这里使用的倒是另外一个函数呢？跳转代码瞅瞅，原来使用的不是标准的协方差计算公式啊。

继续追踪，跳转到了_compute_covariance_auto函数，在这个函数中有不少协方差的计算方法，涨知识了协方差还有这么多计算的道道，原来这叫经验协方差。上面的注释中说是使用sklearn中的计算方式，还真特么有。。。。

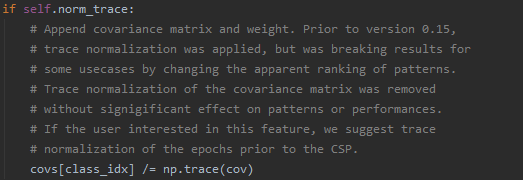
好吧，不纠结了怎么说这也算是协方差，能够接受，继续往下看，看到这部分多少有些安心了，MNE中也提供了利用迹进行正则化的方法，看来整体的思路没错。

下面就是求特征值和特征向量了，这里使用了abs绝对值，也对应了我上面说的特征值排序应该取绝对值。这里为何-0.5就不清楚了。特征提取采用的矩阵相乘，这点前面也解释过，滤波后的数据求协方差不须要减去均值，这里用的也是协方差(能量)的均值做为特征。

不知道你们发现没有这里少了一个步骤就是白化处理，这一点尚未没想明白？难道就是由于它用的协方差计算方法比较牛，而且特征值减去了0.5就不用白化了么？牛皮就是任性啊。。。

patterns和filter的理解

参考说一下我的对这两个参数的理解，测得的数据通过filter滤波后的结果至关因而获得了原始波，而patterns就是源分布信息。

原始波 * 源位置 = 测得的数据

《Optimizing spatial filters for robust EEG single-trial analysis》

《Designing optimal spatial filters for single-trial EEG classification in a movement task》