使用Python，Open3D对点云散点投影到面上并可视化，使用3种方法计算面的法向量及与平均法向量的夹角

使用Python，Open3D对点云散点投影到面上并可视化，使用3种方法计算面的法向量及与平均法向量的夹角

写这篇博客源于博友的提问，他坚定了我继续坚持学习的心，带给了我充实与快乐。
将介绍以下5部分：

1. 随机生成点云点
2. 投影点到面（给出了6个面的中心点，离哪个中心点距离近就投影到哪个面）
3. 对投影到每个面的点云计算法向量点（3种方法 KNN 半径近邻 混合近邻）
4. 对每个面上的法向量及与平均法向量的夹角
5. 可视化原始点及法向量点

1. 效果图

1.1 点云点灰色 VS 法向量点绿色 VS 法向量可视化

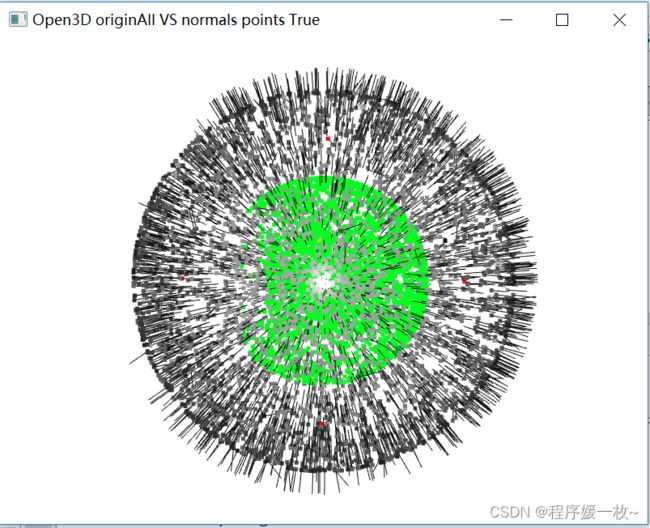
全量点云点灰色 VS 全量法向量点绿色效果图如下：
投影到每个面的均值点为渲染为红色比较明显。法向量点均值点渲染为黄色这里不太明显，可查看下边每个投影面的效果图；

全量点云点灰色 VS 全量法向量点绿色 VS 法向量可视化 效果图如下：

1.2 投影到每个面上的点云点灰色 VS 法向量点绿色 VS 均值点红色，法向量均值点黄色

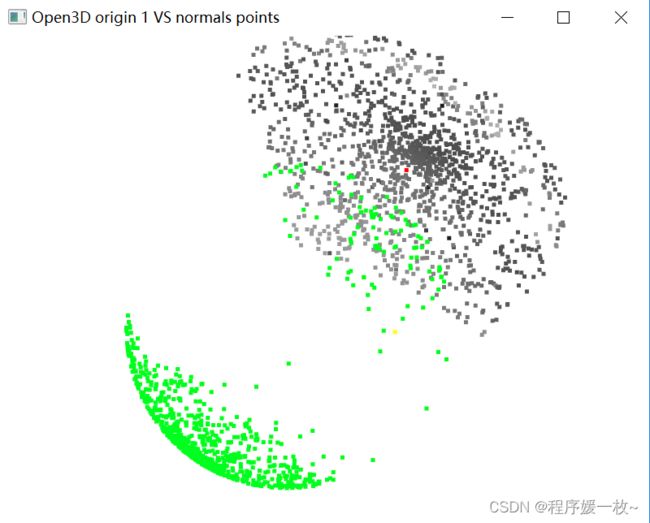
投影到第一个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，如下图
红色，黄色点不明显，旋转下看下一个图；

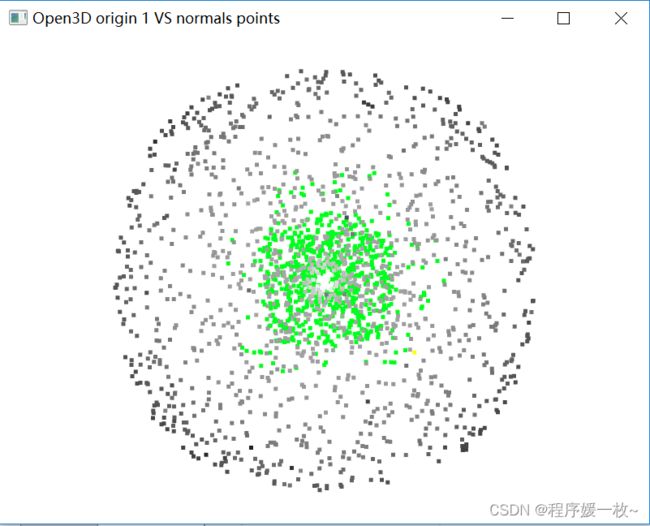
投影到第一个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，旋转后红色、黄色点比较明显 如下图

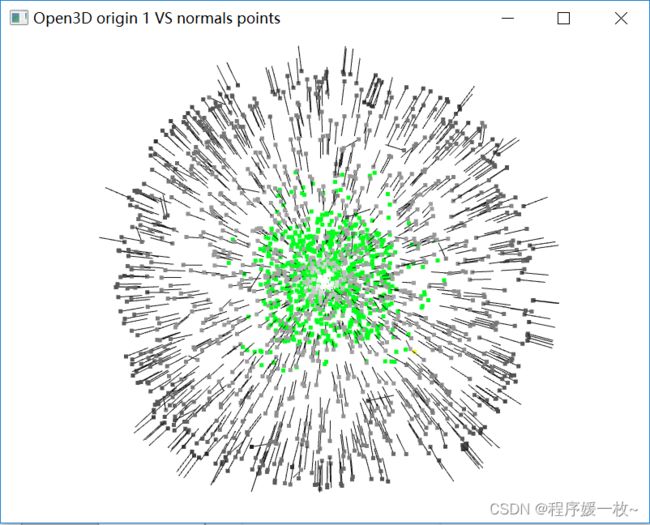
投影到第一个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，同时可视化法向量点 如下图

投影到第2个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，如下图

投影到第2个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，同时渲染法向量 如下图

投影到第3个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，如下图

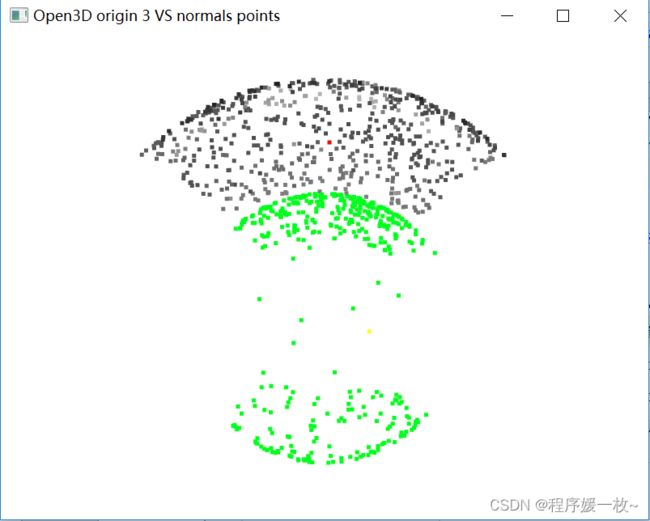
投影到第3个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，同时渲染法向量 如下图

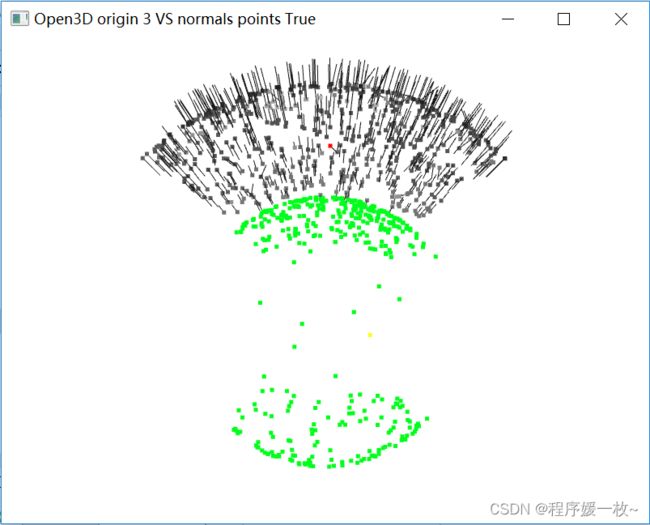
投影到第4个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，如下图

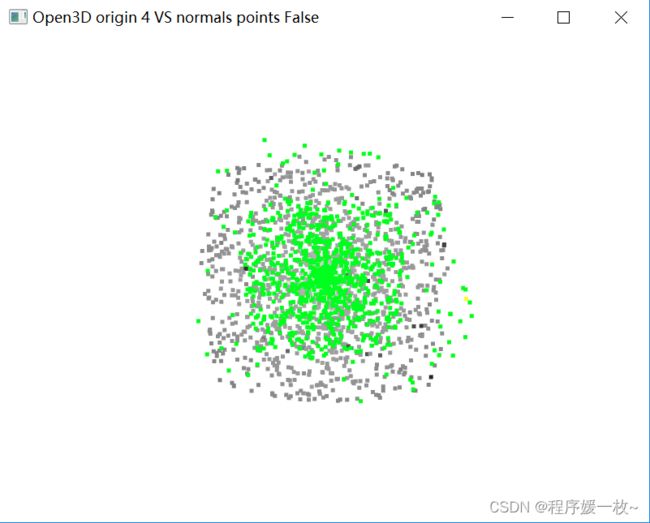
投影到第4个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，同时渲染法向量 如下图

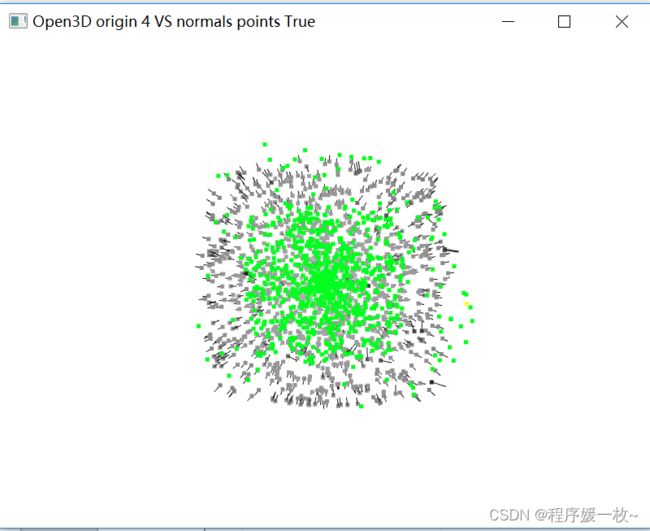
投影到第5个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，如下图

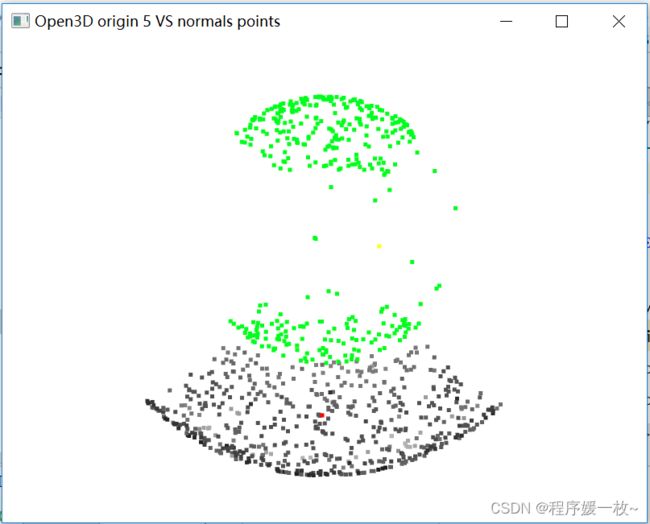
投影到第5个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，同时渲染法向量 如下图

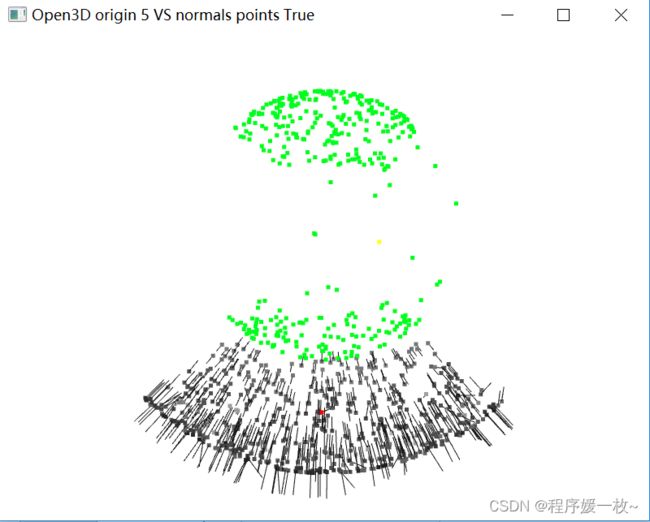
投影到第6个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，如下图

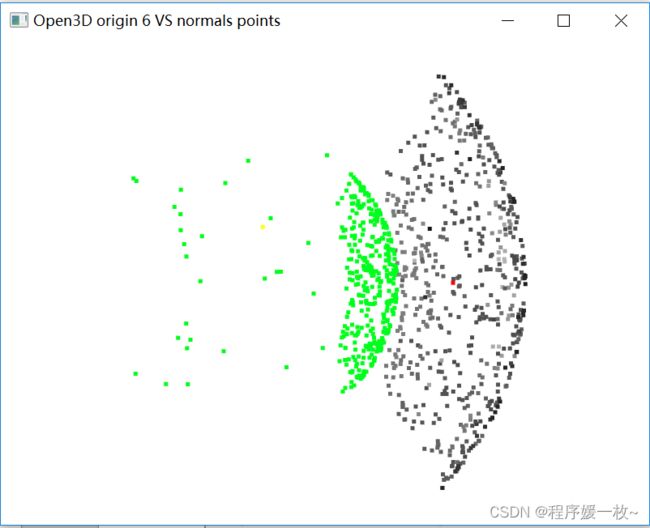
投影到第6个面上的原始点渲染为灰色，均值点渲染为红色；
法向量点渲染为绿色，法向量均值点渲染为黄色，同时渲染法向量 如下图

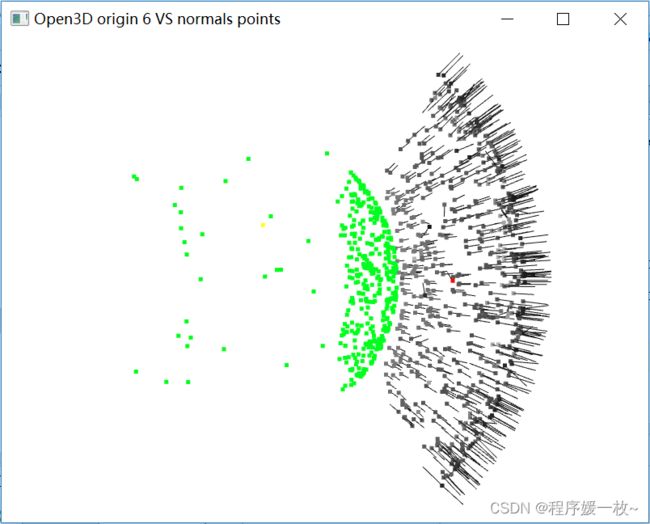
2. 源码

# 随机生成点
# 投影到面上，（给出了6个面的中心点，离哪个中心点距离近就投影到哪个面）
# 对投影到每个面的点云计算法向量点（3种方法 KNN 半径近邻 混合近邻）
# 对每个面上的法向量求均值及与平均法向量的夹角
# 并可视化原始点灰色，法向量点绿色，均值点红色，均值法向量点黄色
import random

import numpy as np
import open3d as o3d

# 随机种子，以便复现结果
random.seed(123)

# 假设立方体是2*2*2，立方体的质心是笛卡尔坐标的原点，立方体外接球的半径为sqrt（3）

d = {}  # 存储面的中心点及投影到每个面上的点云点，key中心 values投影到该面的点云点


def add_dict(dictionary, loc, centroid):
    # loc is the point's location on sphere,
    # centroid is the center(s) of cube's face(s) that is nearest to the loc
    if tuple(loc) in dictionary.keys():
        dictionary[tuple(loc)].append(list(centroid))
    else:
        dictionary[tuple(loc)] = [list(centroid)]


def point_generator(npoints, r):
    result = []
    # 0 < theta < 2*np.pi
    # 0 < phi < np.pi
    for i in range(npoints):
        theta = random.random() * 2 * np.pi
        phi = random.random() * np.pi
        x = r * np.cos(theta) * np.sin(phi)
        y = r * np.sin(theta) * np.sin(phi)
        z = r * np.cos(phi)
        result.append([x, y, z])
    return result


npoints = 5000
r = np.sqrt(3)
centroids = [[1, 0, 0], [0, 1, 0], [0, 0, 1], [-1, 0, 0], [0, -1, 0], [0, 0, -1]]
points = point_generator(npoints, r)


# print(points)

# 计算俩个点的距离
def distance(p, q):
    if len(p) == len(q):
        result = 0
        for i in range(len(p)):
            result += (p[i] - q[i]) ** 2
        return result ** 0.5
    else:
        print('cannot calculate distance of points from different dimensions')


# 寻找离点最近的面（中心点），并投影到对应的面上
def archive_nearest_pc_pairs(dictionary, centroids, points):
    for p in points:
        dist = []
        for q in centroids:
            dist.append(distance(p, q))
        nearest_centroid = centroids[dist.index(min(dist))]  # 寻找最近的立方体面中心的点距离
        add_dict(dictionary, nearest_centroid, p)


archive_nearest_pc_pairs(d, centroids, points)
print(centroids)


# 3种方法计算法向量
def compute_normals(pcd, flag=1):
    # 混合搜索  KNN搜索  半径搜索
    if (flag == 1):
        pcd.estimate_normals(
            search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.01, max_nn=20))  # 计算法线,搜索半径1cm,只考虑邻域内的20个点
    elif (flag == 2):
        pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamKNN(knn=3))  # 计算法线,只考虑邻域内的20个点
    else:
        pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamRadius(radius=0.01))  # 计算法线,搜索半径1cm,只考虑邻域内的20个点


# 计算俩个法向量的夹角可参考 http://mp.ofweek.com/it/a456714148137
# x为第一个法向量，y为第二个法向量
def cal_angle(x, y):
    # 分别计算两个向量的模：
    l＿x = np.sqrt(x.dot(x))
    l＿y = np.sqrt(y.dot(y))
    # print('向量的模=', l＿x, l＿y)

    # 计算两个向量的点积
    dian = x.dot(y)
    # print('向量的点积=', dian)

    # 计算夹角的cos值：
    cos＿ = dian / (l＿x * l＿y)
    # print('夹角的cos值=', cos＿)

    # 求得夹角(弧度制)：
    angle＿hu = np.arccos(cos＿)
    # print('夹角(弧度制)=', angle＿hu)

    # 转换为角度值：
    angle＿d = angle＿hu * 180 / np.pi
    # print('夹角=%f°' % angle＿d)
    return angle＿d


# 初始化法向量dict，key中心点 values法向量点
normals_dict = {}
pcds = []
for i, (key, value) in enumerate(d.items()):
    # print(value)
    val = np.array(value)

    # 计算点云均值点，并插入到原点云点的第一个点
    avg_point = np.mean(val, axis=0)  # axis=0,计算每一列的均值
    origin_points = np.row_stack((avg_point, val))

    # 构造点云数据
    pcd = o3d.geometry.PointCloud()
    points = o3d.utility.Vector3dVector(origin_points)
    pcd.points = points

    # 计算法向量,可选择3种方法计算法向量,传值1/2/其他
    compute_normals(pcd, 2)
    normals = o3d.np.asarray(pcd.normals)
    # print('pcd-normals: ', normals)
    normals_dict[key] = normals
    print('第', str(i + 1), '个面, center:', key, len(pcd.normals), '个点')
    # print(np.sum(normals) / len(normals))

    # 均值点法向量点
    avg_normal = normals[0]

    # 遍历计算平均向量与点云向量的夹角（由于第一个点是均值点，所以去除）
    for j, (point, point_normal) in enumerate(zip(origin_points[1:], normals[1:])):
        # 计算均值点法向量 与 点云点法向量的夹角
        print('\t第 %s 个点, angle: %s' % (
            str(j + 1),
            cal_angle(np.array(avg_point) - np.array(avg_normal), np.array(point) - np.array(point_normal))))
    print("--------------------------------------------------------")

    # 可视化法向量点和原始点
    pcd.paint_uniform_color([0.5, 0.5, 0.5])  # 把原始点渲染为灰色
    pcd.colors[0] = [1, 0, 0]  # 原始点云均值点渲染为红色
    normal_point = o3d.utility.Vector3dVector(pcd.normals)
    normals = o3d.geometry.PointCloud()
    normals.points = normal_point
    normals.paint_uniform_color((0, 1, 0))  # 点云法向量的点都以绿色显示
    normals.colors[0] = [1, 1, 0]  # 均值点法向量点渲染为黄色
    o3d.visualization.draw_geometries([pcd, normals], "Open3D origin " + str(i + 1) + " VS normals points True",
                                      width=800,
                                      height=600, left=50,
                                      top=50,
                                      point_show_normal=True, mesh_show_wireframe=False,
                                      mesh_show_back_face=False)
    o3d.visualization.draw_geometries([pcd, normals], "Open3D origin " + str(i + 1) + " VS normals points False",
                                      width=800,
                                      height=600, left=50,
                                      top=50,
                                      point_show_normal=False, mesh_show_wireframe=False,
                                      mesh_show_back_face=False)

    # 加入list以便全量渲染
    pcds.append(pcd)
    pcds.append(normals)

print(pcds[0], pcds[1], pcds[2], pcds[3], pcds[4], pcds[5],
      pcds[6], pcds[7], pcds[8], pcds[9], pcds[10], pcds[11],
      len(pcds))
# 同时可视化法向量
o3d.visualization.draw_geometries([pcds[0], pcds[1], pcds[2], pcds[3], pcds[4],
                                   pcds[5], pcds[6], pcds[7], pcds[8], pcds[9], pcds[10], pcds[11]
                                   ], "Open3D originAll VS normals points True",
                                  width=800,
                                  height=600, left=50,
                                  top=50,
                                  point_show_normal=True, mesh_show_wireframe=False,
                                  mesh_show_back_face=False)

# 不可视化法向量
o3d.visualization.draw_geometries([pcds[0], pcds[1], pcds[2], pcds[3], pcds[4],
                                   pcds[5], pcds[6], pcds[7], pcds[8], pcds[9],
                                   pcds[10], pcds[11]], "Open3D originAll VS normals points False",
                                  width=800,
                                  height=600, left=50,
                                  top=50,
                                  point_show_normal=False, mesh_show_wireframe=False,
                                  mesh_show_back_face=False)

参考

• 计算俩个法向量的夹角可参考 http://mp.ofweek.com/it/a456714148137