提升目标检测模型性能的tricks
提升目标检测模型性能的tricks
- bag of freebies
-
- pixel-wise调整
-
- 几何畸变
- 光照变化
- 遮挡
-
- Random Erase
- CutOut
- Hide-and-Seek
- Grid Mask
- 正则
-
- Dropout
- DropConnect
- DropBlock
- 用多张图来进行增强
-
- Mixup
- CutMix
- Mosaic数据增强
- GAN——Style Transfer GAN
- 数据分布不平衡
-
- 两阶段
-
- Hard Negative Example Mining
- Online Hard Example Mining
- 单阶段——Focal loss
- one-hot类别之间没有关联
-
- Label Smoothing
- 知识蒸馏
- BBox回归
-
- IoU Loss
- GIoU Loss
- DIoU Loss
- CIoU Loss
- BoS
-
- 即插即用模块
-
- 提升模型感受野
-
- SPP
- RFB
- ASPP
- 注意力机制
-
- SE
- SAM——spatial attention
- modified SAM——point-wise attention
- 特征融合模块
-
- Skip Connection
- Hyper Column
- FPN
-
- SFAM
- ASFF
- BiFPN
- 激活函数
-
- ReLU
- LReLU
- PReLU
- ReLU6
- SELU
- Swish
- Hard Swish
- Mish
- 后处理方法——NMS
-
- gredy NMS
- Soft NMS
-
- 线性NMS
- 高斯NMS
- 缺点
- DIOU NMS
bag of freebies
BoF(bag of freebies):指那些能够提高精度而不增加推断时间的技术
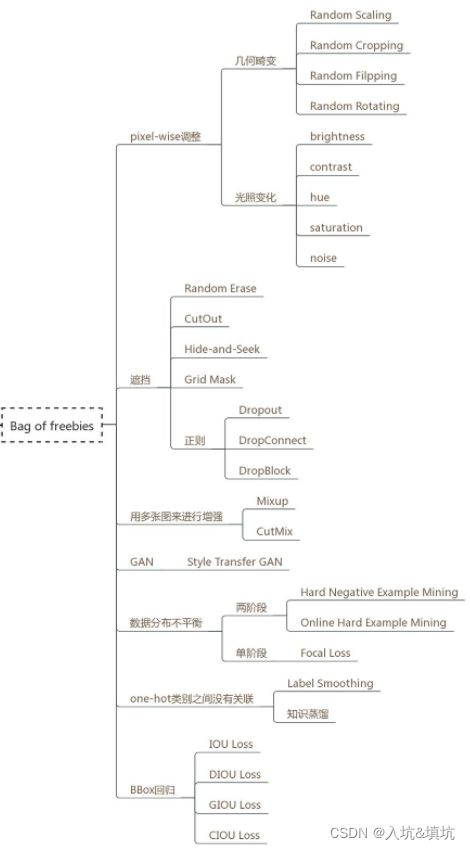
pixel-wise调整
pixel-wise调整主要是指图像增强部分,通过提高数据的复杂度来提升模型的鲁棒性。
几何畸变
几何畸变主要包括随机缩放(Random Scaling)、随机裁剪(Random Cropping)、随机翻转(Random Filpping)、随机旋转(Random Rotating)
光照变化
光照变化主要包括调整亮度(brightness)、对比度(contrast)、色调(hue)、饱和度(saturatuion)以及添加噪声(noise)
遮挡
除了正则外,其余的其实是数据增强的方法,只是有点正则的味道。
Random Erase
Random Erase称为随机擦除,随机选择一个区域,采用随机值进行覆盖,所选区域一定在图像内。把物体遮挡一部分也能被正确识别分类,这样就迫使网络利用局部数据进行训练识别,增大了训练难度,一定程度提高模型的泛化能力。

CutOut
随机选择一个固定大小的正方形区域,像素值全部用0填充即可,但为了避免0填充对训练数据有影响,需要对训练数据进行归一化处理,norm到0,但需要注意的是,随机选择的区域可能不在图像内,也就是说正方形区域可能只有部分处理图像内,因而模拟了任意形状的擦除操作。

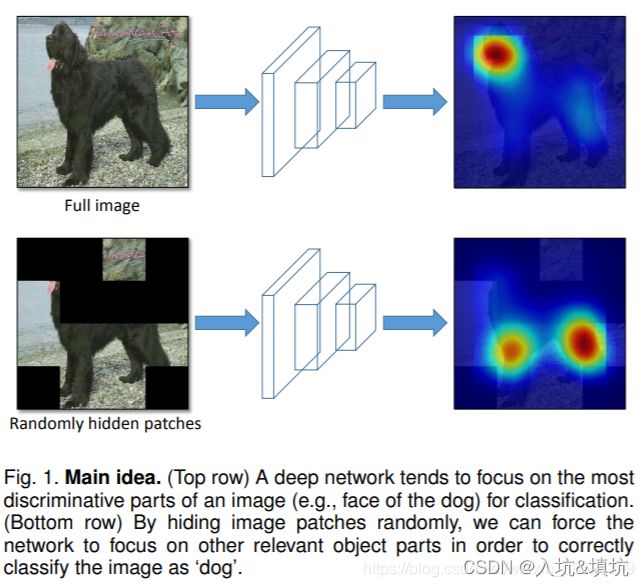
Hide-and-Seek
将图像切分成S*S网络,每个网络使用一定概率进行遮挡,从而模拟出Random Erase和CutOut的效果。
但是遮挡值设置为何值比较关键,如果填0或者255都可能改变训练集的数据分布,作者经过计算,采用整个数据集的均值影响最小。
Grid Mask
该方法是前三个遮挡方法的改进,因为Random Erase、CutOut和Hide-and-Seek都可能存在一个问题,就是把图像的可判别区域全部删除或者保留,引入噪声并且效果不佳。

为了解决上述问题,对删除信息和保留信息之间进行权衡,Grid Mask采用结构化drop操作,例如均匀分布地删除正方形区域,并且通过控制密度和size参数,来达到平衡,密度就是正方形个数,size就是正方形大小。

正则
Dropout
将神经元输出随机置0,只能在FC里使用。
DropConnect
随机将神经元内的权重置0。
比如原来某一个神经元内的权重为 [ w 1 , w 2 , w 3 ] [w_1,w_2,w_3] [w1,w2,w3],那么原来的输出是 w 1 x 1 + w 2 x 2 + w 3 x 3 w_1x_1+w_2x_2+w_3x_3 w1x1+w2x2+w3x3,假设使用DropConnect后,该神经元内w_2被置0,那么输出变成 w 1 x 1 + 0 ∗ x 2 + w 3 x 3 w_1x_1+0*x_2+w_3x_3 w1x1+0∗x2+w3x3,而Dropout是直接将这个神经元的输出直接随机置0。
只能在FC中用,
DropBlock
DropBlock是适用于卷积层的正则化方法,它作用的对象的特征图。在DropBlock中,特征在一个个block中,当应用DropBlock时,一个feature map中的连续区域会一起被drop掉。那么模型为了拟合数据网络就不得不往别处看,以寻找新的证据。
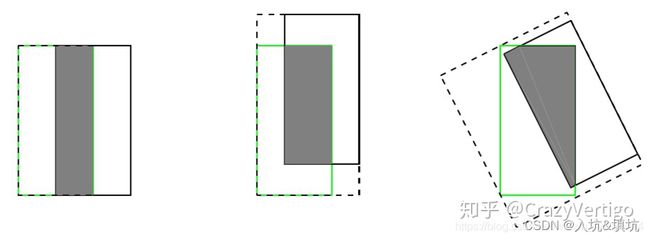
(a)原始输入图像
(b)绿色部分表示激活的特征单元,b图表示了随机dropout激活单元,但是这样dropout后,网络还会从drouout掉的激活单元附近学习到同样的信息(相邻信息的感受野具有一定的重叠,导致信息具有一定的相似性)。
©绿色部分表示激活的特征单元,c图表示本文的DropBlock,通过dropout掉一部分相邻的整片的区域(比如头和脚),网络就会去注重学习狗的别的部位的特征,来实现正确分类,从而表现出更好的泛化。
用多张图来进行增强
将多张图片融合一起的数据增强操作
Mixup
将两张图片采用比例混合,label也按照比例混合。
label按照比例混合,例如两张图里的同一块区域里一个label的one-hot是 y 1 = [ 0 , 1 , 0 ] y1=[0,1,0] y1=[0,1,0],另一个label的one-hot是 y 2 = [ 1 , 0 , 0 ] y2=[1,0,0] y2=[1,0,0],加入 λ = 0.2 \lambda=0.2 λ=0.2,则混合后的label的one-hot为 y 3 = 0.2 y 1 + 0.8 y 2 = [ 0.8 , 0.2 , 0 ] y3=0.2y1+0.8y2=[0.8,0.2,0] y3=0.2y1+0.8y2=[0.8,0.2,0]
CutMix
CutMix是CutOut和Mixup的结合,将图片的一部分区域擦除并随机填充训练集中的其他数据区域像素值。

Mosaic数据增强
Mosaic数据增强是CutMix的拓展,CutMix是混合两张图,Mosaic数据增强是混合了四张具有不同语义信息的图片,可以让检测器检测出超乎常规语境的目标,增强鲁棒性,并减少对大的mini-batch的依赖。

GAN——Style Transfer GAN
论文:ImageNet-trained cnns are biased towards texture; increasing shape bias improves accuracy and robustness
论文发现CNN训练学习到的实际是纹理特征(texture bias)而不是形状特征,这与人类的认知相反,因而通过GAN引入风格化的ImageNet数据集,平衡纹理和形状偏置,提高模型的泛化能力。
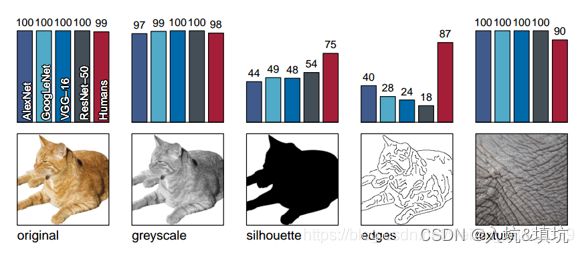
作者使用了6份数据,正常的猫、灰度图、只包含轮廓的、只包含边缘的、只有纹理没有形状的、猫的形状大象的纹理的,由结果可知,对于正常的图片和灰度图,网络识别率都很高,对于只包含轮廓和边缘的,网络识别率较低,对于只包含纹理的,网络识别率也较高。对于猫的形状大象的纹理的图片,网络误识别为大象的概率较高,因而可以推断网络学习的实际是纹理特征。
因而可以通过GAN随机将物体的纹理替换,从而增强网络的学习特征能力。
数据分布不平衡
两阶段
Hard Negative Example Mining
难例挖掘(Hard Negative Example Mining)与非极大值抑制 NMS 一样,都是为了解决目标检测老大难问题(样本不平衡+低召回率)及其带来的副作用。
难负例挖掘(Hard Negative Mining)就是在训练时,尽量多挖掘些难负例(hard negative)加入负样本集,这样会比easy negative组成的负样本集效果更好。(其实就是加入大量背景图像作为负样本,让模型在学习如何分类对象的同时也学习对背景的分类。个人觉得之所以要加入比正样本多得多的大量负样本,是因为背景的复杂性性比正样本要多得多,在目标检测中一般都是粗粒度的检测,正样本的复杂性相对较低,细粒度的另论)
Online Hard Example Mining
OHEM主要思想是,根据输入样本的损失进行筛选,筛选出hard example,表示对分类和检测影响较大的样本,然后将筛选得到的这些样本应用在随机梯度下降中训练。在实际操作中是将原来的一个ROI Network扩充为两个ROI Network,这两个ROI Network共享参数。其中前面一个ROI Network只有前向操作,主要用于计算损失;后面一个ROI Network包括前向和后向操作,以hard example作为输入,计算损失并回传梯度。这种算法的优点在于,对于数据的类别不平衡问题不需要采用设置正负样本比例的方式来解决,且随着数据集的增大,算法的提升更加明显。
注:OHEM是根据负样本的loss(只到计算loss,还不向后更新参数)来选择更新参数的负样本,而难例挖掘是直接输入一大堆负样本,不管它们对网络更新权重的贡献情况。OHEM的优点是不需要输入大量的负样本,训练的时候可以比较快。
单阶段——Focal loss
Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重,也可理解为一种困难样本挖掘。
交叉熵: C E = − ( y l o g p − ( 1 − y ) l o g ( 1 − p ) ) = { − l o g p , if y = 1 − l o g ( 1 − p ) , if y = 0 CE=-(ylogp-(1-y)log(1-p))=\begin{cases} -logp, & \text{if $y=1$ } \\ -log(1-p), & \text{if $y=0$ } \\ \end{cases} CE=−(ylogp−(1−y)log(1−p))={−logp,−log(1−p),if y=1 if y=0
Focal loss:在原有的基础上加了一个因子,其中gamma>0使得减少易分类样本的损失。使得更关注于困难的、错分的样本。
F L = { − ( 1 − p ) γ l o g p , if y = 1 − p γ l o g ( 1 − p ) , if y = 0 FL=\begin{cases} -(1-p)^{\gamma}logp, & \text{if $y=1$ } \\ -p^{\gamma}log(1-p), & \text{if $y=0$ } \\ \end{cases} FL={−(1−p)γlogp,−pγlog(1−p),if y=1 if y=0
甚至还可以加入 α \alpha α来平衡正负样本本身的比例不均(添加alpha虽然可以平衡正负样本的重要性,但是无法解决简单与困难样本的问题):
F L = { − α ( 1 − p ) γ l o g p , if y = 1 − ( 1 − α ) p γ l o g ( 1 − p ) , if y = 0 FL=\begin{cases} -\alpha(1-p)^{\gamma}logp, & \text{if $y=1$ } \\ -(1-\alpha)p^{\gamma}log(1-p), & \text{if $y=0$ } \\ \end{cases} FL={−α(1−p)γlogp,−(1−α)pγlog(1−p),if y=1 if y=0
注:实验发现 γ \gamma γ为2是最优
one-hot类别之间没有关联
Label Smoothing
在交叉熵中,神经网络会促使自身往正确标签和错误标签差值最大的方向学习,在训练数据较少,不足以表征所有的样本特征的情况下,会导致网络过拟合。
label smoothing为了解决上述问题提出了通过soft one-hot来加入噪声(其实也是正则化策略),减少了真实样本标签的类别在计算损失函数时的权重,最终起到抑制过拟合的效果。
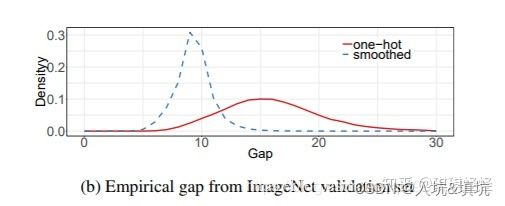
在多分类里的交叉熵loss为:
l o s s = − ∑ i = 1 K p i l o g q i , p i = { 1 , if i = y 0 , if i ≠ y loss=-\sum^K_{i=1}p_ilogq_i, p_i=\begin{cases} 1, & \text{if $i=y$ } \\ 0, & \text{if $i\neq y$ } \\ \end{cases} loss=−i=1∑Kpilogqi,pi={1,0,if i=y if i=y
最优预测概率为:
Z i = { + ∞ , if i = y 0 , if i ≠ y Z_i=\begin{cases} +\infty, & \text{if $i=y$ } \\ 0, & \text{if $i\neq y$ } \\ \end{cases} Zi={+∞,0,if i=y if i=y
Label Smoothing将真实的概率分布变成:
p i = { 1 − ϵ , if i = y ϵ K − 1 , if i ≠ y p_i=\begin{cases} 1-\epsilon, & \text{if $i=y$ } \\ \frac{\epsilon}{K-1}, & \text{if $i\neq y$ } \\ \end{cases} pi={1−ϵ,K−1ϵ,if i=y if i=y
K 表 示 多 分 类 的 类 别 总 数 K表示多分类的类别总数 K表示多分类的类别总数, ϵ \epsilon ϵ是一个较小的超参数
loss就变成:
l o s s i = { ( 1 − ϵ ) ∗ l o s s , if i = y ϵ ∗ l o s s , if i ≠ y loss_i=\begin{cases} (1-\epsilon)*loss, & \text{if $i=y$ } \\ \epsilon*loss, & \text{if $i\neq y$ } \\ \end{cases} lossi={(1−ϵ)∗loss,ϵ∗loss,if i=y if i=y
最优预测概率变成:
Z i = { l o g ( k − 1 ) ( 1 − ϵ ) ϵ + α , if i = y α , if i ≠ y Z_i=\begin{cases} log\frac{(k-1)(1-\epsilon)}{\epsilon+\alpha}, & \text{if $i=y$ } \\ \alpha, & \text{if $i\neq y$ } \\ \end{cases} Zi={logϵ+α(k−1)(1−ϵ),α,if i=y if i=y
α \alpha α是任意实数,最终模型通过抑制正负样本输出差值,使得网络有更强的泛化能力
知识蒸馏
在知识蒸馏里面有2个模型:Teacher和Student
Teacher是一个复杂但高精度的模型
Student是一个精简、低复杂度、易部署的模型
实际要训练的Student模型
将每一个样本输入Student里计算loss的时候需要计算2个loss:Soft loss和Hard loss
Hard loss是指loss的real target为ground truth。
Soft loss是指loss的real target为Teacher的prediction,具体的soft内容如下:
Teacher在输出predict前需要在最后softmax前先除以T,再softmax,然后输出prediction(此时就是soft real target)。
Student的soft prediction和Teacher一样,在进行最后一层的softmax前也先除以T,再softmax,然后再输出prediction。
total loss = λ soft loss + ( 1 − λ ) hard loss \text{total loss}=\lambda\text{ soft loss}+(1-\lambda)\text{ hard loss} total loss=λ soft loss+(1−λ) hard loss
T数值越大,分布越缓和;而T数值减小,容易放大错误分类的概率,引入不必要的噪声(训练的时候可以一开始大点,然后慢慢变小)。针对较困难的分类或检测任务,T通常取1,确保教师网络中正确预测的贡献。硬目标则是样本的真实标注,可以用One-hot矢量表示。Total loss设计为软目标与硬目标所对应的交叉熵的加权平均(表示为KD loss与CE loss),其中软目标交叉熵的加权系数越大,表明迁移诱导越依赖教师网络的贡献,这对训练初期阶段是很有必要的,有助于让学生网络更轻松的鉴别简单样本,但训练后期需要适当减小软目标的比重(减少计算soft loss的样本),让真实标注帮助鉴别困难样本。另外,教师网络的预测精度通常要优于学生网络,而模型容量则无具体限制,且教师网络推理精度越高,越有利于学生网络的学习。
BBox回归
IoU Loss
IoU Loss考虑了预测BBox区域和ground truth的覆盖范围,解决传统方法在计算{x, y, w, h}的L1 loss 或者 L2loss时,并没有考虑靠坐标之间的相关性(损失会随着尺度的增大而增大)的问题。
IoU loss = − l o g I n t e r s e c t i o n U n i o n = 1 − I o U \text{IoU loss}=-log\frac{Intersection}{Union}=1-IoU IoU loss=−logUnionIntersection=1−IoU
Intersection:两个框的相交面积
Union:两个框的相并面积
IoU_loss缺点:
- 当预测框和目标框不相交时,IoU(A,B)=0时,不能反映A,B距离的远近,此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。
- 假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,其IoU值是相同时,IoU值不能反映两个框是如何相交的。
GIoU Loss
GIoU loss = I o U − A c − u A c \text{GIoU loss}=IoU-\frac{A^c-u}{A^c} GIoU loss=IoU−AcAc−u
− 1 ≤ G I o U l o s s ≤ 1 -1\leq GIoU loss\leq1 −1≤GIoUloss≤1
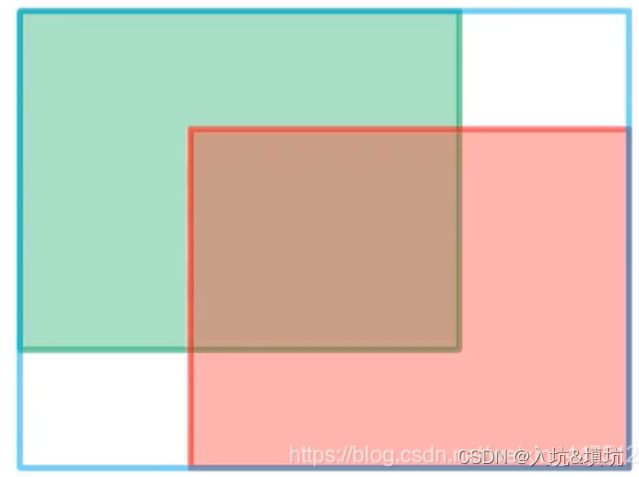
A c A^c Ac指的是如图所示的外围蓝色的边界框; u u u指的是预测边界框与真实边界框之间的并集面积。当两个边界框处于同一水平线或者是同一竖直线上时,会退化成IoU
GIoU考虑了两个框的中心和角度是否对齐。
DIoU Loss
DIoU Loss考虑了两个框之间的重叠面积和中心点距离,相对于GIoU Loss收敛速度更快,但没有考虑到长宽比。
DIoU loss = 1 − I o U + ρ 2 ( b , b g t ) c 2 \text{DIoU loss}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2} DIoU loss=1−IoU+c2ρ2(b,bgt)
DIoU中的惩罚项表示为 R D I o U = ρ 2 ( b , b g t ) c 2 R_{DIoU}=\frac{\rho^2(b,b^{gt})}{c^2} RDIoU=c2ρ2(b,bgt),其中 b b b和 b g t b^{gt} bgt分别表示预测的BBox和ground truth BBox的中心点, ρ ( ⋅ ) \rho(\cdot) ρ(⋅)表示欧式距离, c c c表示预测的BBox和ground truth BBox的的最小外接矩形的对角线距离,如下图所示。可以将DIoU替换IoU用于NMS算法当中,也即论文提出的DIoU-NMS,实验结果表明有一定的提升。
(上图中绿色框为目标框,黑色框为预测框,灰色框为两者的最小外界矩形框,d表示目标框和真实框的中心点距离,c表示最小外界矩形框的距离。)
其实,DIoU的损失函数也就是: DIoU loss = 1 − I o U + d 2 c 2 \text{DIoU loss}=1-IoU+\frac{d^2}{c^2} DIoU loss=1−IoU+c2d2
其中的 d d d为两个框的中心距离; c c c表示最小外界矩阵的对角线距离。
CIoU Loss
CIou Loss改进了DIOU Loss,把重叠面积,中心点距离,长宽比都考虑进来了,可以在BBox回归问题上获得更好的收敛速度和精度。
CIoU loss = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v \text{CIoU loss}=1-IoU+\frac{\rho^2(b,b^{gt})}{c^2}+\alpha v CIoU loss=1−IoU+c2ρ2(b,bgt)+αv
其中: α = v 1 − I o U \alpha=\frac{v}{1-IoU} α=1−IoUv, v = 4 π ( a r c t a n w g t h g t − a r c t a n w h ) 2 v=\frac{4}{\pi}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})^2 v=π4(arctanhgtwgt−arctanhw)2
BoS
BoS(bag of specials):指增加稍许推理代价,但可以提高模型精度的方法
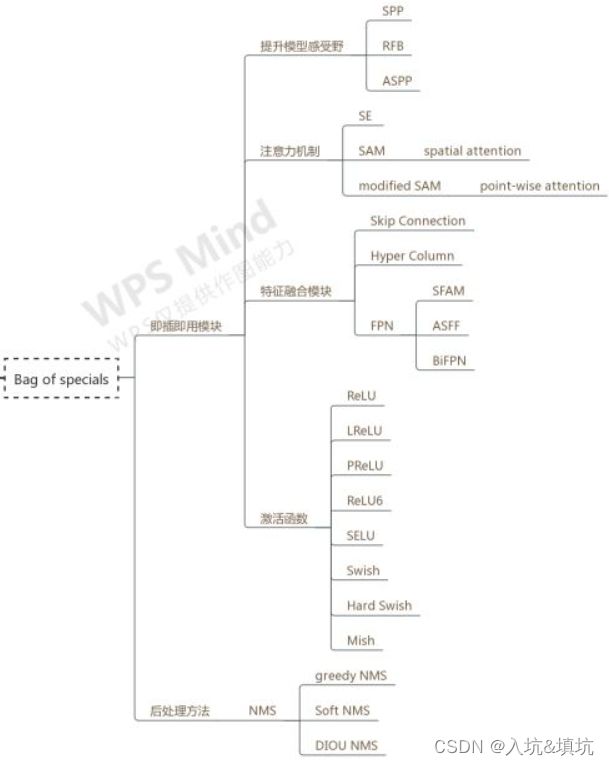
即插即用模块
提升模型感受野
SPP
SPPNet称为空间金字塔池化网络,其思路其实很简单,就是为了让网络能够适应不同尺度的图像输入,避免对图片进行裁剪或者缩放,导致位置信息丢失。
由于卷积层在面对不同尺度的输入图像时,会生成大小不一样的特征图,会对网络的训练带来较大的麻烦,因而SPPNet就通过将卷积层最后一层的池化层替换为金字塔池化层,固定输入的特征向量的大小。(根据预设池化结果的尺度和输入特征的尺度计算出实际池化时的尺度和步长,然后得到和预设尺度相同的结果,最后合并成一个作为FC的输入)

如上图,预设里有3种尺度的池化输出:1x1、2x2、4x4
假如左后一层卷积输出的尺度为axb(a,b至少要大于预设里的最大尺度,不然那生成不了)
生成1x1使用 a a ax b b b尺度的池化,步长为1(其实就不需要步长);
生成2x2使用 ⌈ a 2 ⌉ \lceil\frac{a}{2}\rceil ⌈2a⌉x ⌈ b 2 ⌉ \lceil\frac{b}{2}\rceil ⌈2b⌉尺度的池化,步长为( a − ⌈ a 2 ⌉ a-\lceil\frac{a}{2}\rceil a−⌈2a⌉, b − ⌈ b 2 ⌉ b-\lceil\frac{b}{2}\rceil b−⌈2b⌉)=( ⌊ a 2 ⌋ \lfloor\frac{a}{2}\rfloor ⌊2a⌋, ⌊ b 2 ⌋ \lfloor\frac{b}{2}\rfloor ⌊2b⌋)
生成4x4使用 ⌈ a 4 ⌉ \lceil\frac{a}{4}\rceil ⌈4a⌉x ⌈ b 4 ⌉ \lceil\frac{b}{4}\rceil ⌈4b⌉尺度的池化,步长为( ⌈ a − ⌈ a 4 ⌉ 4 − 1 ⌉ \lceil\frac{a-\lceil\frac{a}{4}\rceil}{4-1}\rceil ⌈4−1a−⌈4a⌉⌉, ⌈ b − ⌈ b 4 ⌉ 4 − 1 ⌉ \lceil\frac{b-\lceil\frac{b}{4}\rceil}{4-1}\rceil ⌈4−1b−⌈4b⌉⌉)=( ⌈ a − ⌈ a 4 ⌉ 3 ⌉ \lceil\frac{a-\lceil\frac{a}{4}\rceil}{3}\rceil ⌈3a−⌈4a⌉⌉, ⌈ b − ⌈ b 4 ⌉ 3 ⌉ \lceil\frac{b-\lceil\frac{b}{4}\rceil}{3}\rceil ⌈3b−⌈4b⌉⌉)
注:相邻池化结果的感受可以存着重叠但不能出现间隔,所以池化的步长不能超过池化核的尺度,又为了保证重叠的感受野尽可能的少,所以采用上述的计算方法。或者采用加padding的方法来保证不重叠,计算原理为 w ∗ k = a + p w*k=a+p w∗k=a+p,其中 w w w为池化后尺度, k k k为池化核的尺度,是第一个 ∗ w *w ∗w大于等于 a a a的正整数, a a a为输入特征图的尺度, p p p为padding
RFB
RFB的每个分支上使用不同尺度的常规卷积 + 空洞卷积,通过各个分支上各自dilated conv所得到的离心率,来模拟人类的视觉感知模式。
具体方法看下面两图:

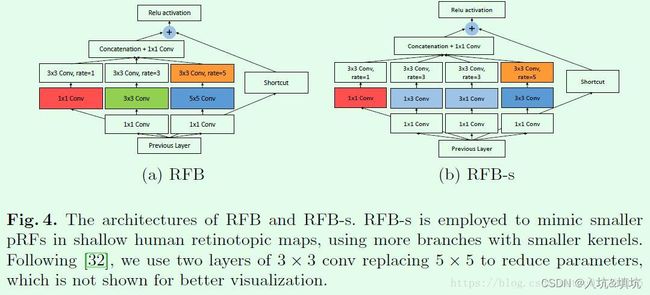
每条支路先采用不同尺度的传统卷积获得不同感受野的特征图,然后再使用空洞卷积来扩大每个信息的感受野,其中每个卷积的步长都为1,并且输出的特征图大小和输入一样,这样最后就能concat。cancat后使用1x1 conv来对特征升维或降维,让它变成和输入特征的通道数一样(为了后面的res),并且对信息跨通道组合。
ASPP
ASPP称为空洞空间金字塔池化网络,与SPP类似的,只是ASPP中采用了空洞卷积对输入的特征图进行不同空洞率进行卷积操作,然后将这些不同空洞率的分支再进行一个融合。由于同一类的物体在图像中可能有不同的比例,ASPP有助于考虑不同的物体比例,这可以提高准确性。(DeepLab v2中就有用到ASPP模块)

注意力机制
SE
SE模块适合使用与CPU,不适合GPU,具体内容看我的另一篇:https://blog.csdn.net/weixin_39994739/article/details/122864848
SAM——spatial attention
SAM(Spatial Attention Module,空间注意力模块)为CBAM中的一部分。
CBAM就是为了解决对特征图内部的空间位置添加权重而提出来的注意力机制模型。它分成了两部分:CAM(Channel Attention Module,通道注意力模块)和SAM。
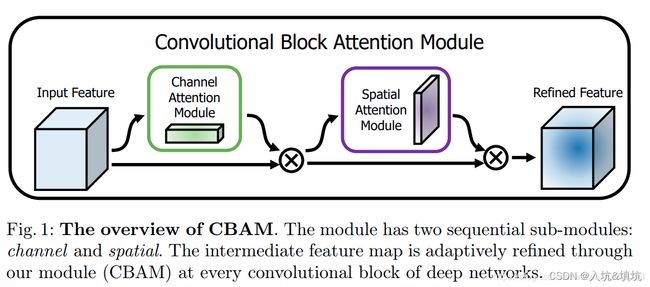
CAM:
CAM和SE的思路几乎差不多,只不过它额外添加了一次全局最大值池化,然后将全局最大值池化得到的C×1×1的特征向量和全局平均池化得到的C×1×1的特征向量依次通过MLP层(也就是SE的FC层,用来先降维后升维,两个向量使用的MLP权重共享),再将输出的特征向量按像素相加,再经过Sigmoid激活与特征图相乘。(与SE的唯一区别就是额外添加了一次全局最大值池化)

SAM:
SAM就是用来对特征图内部的空间位置添加注意力机制的模块,假定输入的特征图还是C×H×W(也就是C张大小为H×W的特征图),这次我们对特征图的每个点(H×W内)进行通道数为C的最大值池化,这样最大值池化输出的特征图大小就是1×H×W,同时也进行通道数为C的平均值池化,输出的特征图大小也是1×H×W,将最大值池化输出的特征图和平均值池化输出的特征图进行拼接形成2×H×W的拼接特征图,然后通过1×1卷积进行通道降维成1×H×W的输出特征图,再经过Sigmoid激活形成空间注意力权重,然后和原来的C×H×W的特征图进行相乘。这样相当于给每张H×W的特征图乘于一个H×W的空间权重,从而形成空间注意力模块。
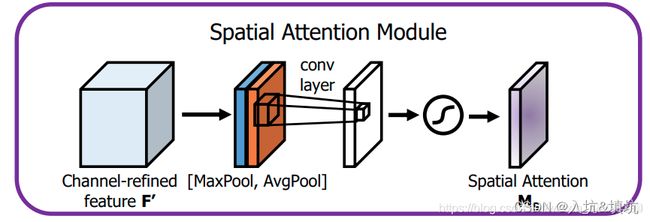
modified SAM——point-wise attention
Modified SAM是YOLOv4的一个创新点,称为像素注意力机制,它的思路也非常简单,就是把SAM模块的池化层全部去除,对C×H×W的特征图进行1×1卷积(既没有降通道也没有升通道),得到C×H×W的输出特征图,然后使用Sigmoid激活,再与原来的C×H×W进行像素点相乘。
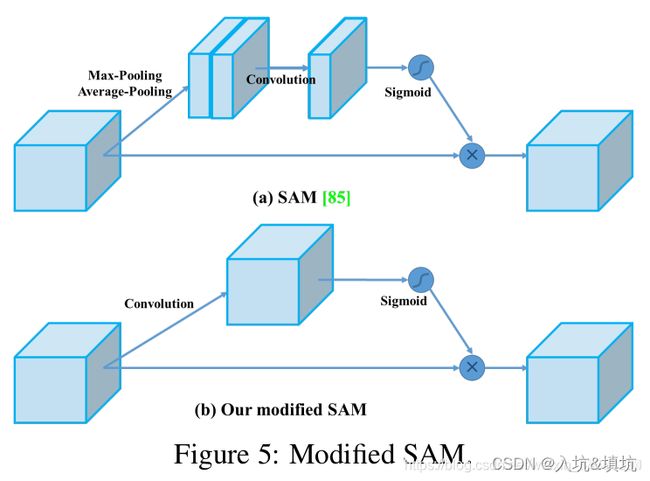
YOLOV4里没有这样修改的好处的解释,这里只是个人见解:点卷积的一个特点是对信息进行跨通道的组合,原来的SAM里点卷积的对象是平均池化与最大值池化后的concat结果,在这里,点卷积能选择的只有2个通道,能选择的少。modified SAM利用这一点给卷积更多的通道去选择来组合更优的结果,并且是每个通道下都组合出一组更优的结果来和输入进行点乘,而SAM只组合出一组作为所有通道下的更优结果(SAM输入只有2通道,而且是均值池化和最大值池化,所以只能组合出一组,多组的结果就有问题了),以一不好代表全部。
特征融合模块
Skip Connection
残差,没什么可说的,想了解看:https://blog.csdn.net/weixin_39994739/article/details/122864848
Hyper Column
超列(hypercolumn),指一个输入像素位置往后的所有对应位置的卷积网络单元激活值,组成一列向量。超列,借鉴于神经科学,其区别在于不仅仅指边缘检测器,还包含更多具有语义信息的神经单元。超列的idea,如下图所示:
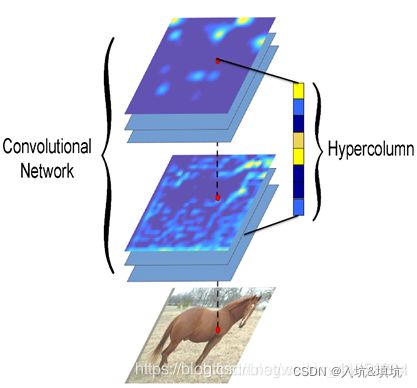
超列的计算,是取得一个检测框(可能是正方形),resize到分类网络的固定输入大小(分类网络使用了全连接层),resized图像分块进入分类网络,把各个层的特征图进行bilinear插值,恢复到图像分块大小,取得各个层的对应位置的超列(级联多通道激活值)。
Hyper Column用于检测分割,由于深层语义信息在精确定位上是不够的,而浅层统计信息则提供了帮助。Hyper利用浅层信息辅助深层语义信息来预测heatmap。
FPN
FPN:特征金字塔,将低分辨率、强语义特征与高分辨率、弱语义特征通过自顶向下的路径和横向连接相结合,从而进行特征融合。

其思路其实就是将高层的特征图进行2倍上采样后和低层的特征图进行相加操作,由于特征图的通道数不匹配,因而需要使用1×1的卷积对低层的特征图进行通道数匹配,这样高层的语义信息就能传递到底层的特征图中,与低层的位置信息相融合,就能得到分类正确且位置精确的目标检测物体。
注意:
- 每层的金字塔设置单一尺度的候选框
- {P2、P3、P4、P5、P6}对应的候选框大小为{ 3 2 2 32^2 322, 6 4 2 64^2 642, 12 8 2 128^2 1282, 25 6 2 256^2 2562, 51 2 2 512^2 5122 },纵横比为{1:2,1:1,2:1}
SFAM
SFAM的主要思想是利用SE模块对多尺度级联特征映射进行通道级加权。
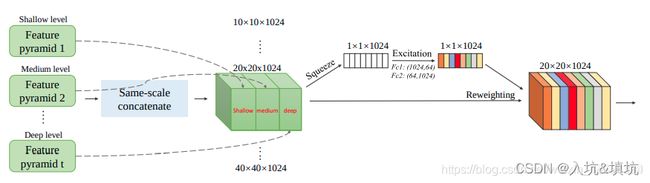
SFAM来源于M2Det,在M2Det中有8个TUM模块,分别会产生6种形状的特征图,SFAM就是将所有TUM中相同形状的特征图拼接一起,然后利用SE模块对多尺度级联特征映射进行通道级加权。
每个TUM模块产生的特征图均是128×S×S(S为1,3,5,10,20,40),因而通道拼接后大小为128×8=1024,与图示相同。。
在检测阶段,在6层特征金字塔后面接两个卷积层来进行位置回归和分类,六个特征图的默认框的检测范围遵循原始SSD的设置。在特征图的每个点,设置三种不同比例总共六个锚点框。之后,使用0.05的概率分数作为阈值来过滤掉分数较低的大多数锚点。使用soft-NMS作为后处理过程。
M2Det具体看:https://blog.csdn.net/weixin_39994739/article/details/123460833
ASFF
ASFF通过学习权重参数的方式将不同层的特征融合到一起,作者证明了这样的方法要优于通过concatenation或者element-wise的方式。
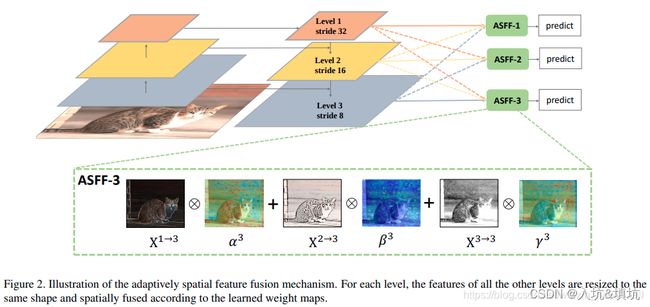
ASFF称为自适应空间特征融合,其思路非常简单,就是为了改进FPN进行特征融合时只是暴力地将高层特征图上采样然后进行像素级的相加操作。ASFF通过对每张融合的特征图设置自学习的权重来进行加权融合。
例如上图中有三张不同尺度的特征图,称为Level1、Level2、Level3,分别 α 3 \alpha_3 α3, β 3 \beta_3 β3和 γ 3 \gamma_3 γ3相乘在相加,就构成了ASFF-3,并且参数 α \alpha α, β \beta β和 γ \gamma γ经过concat之后通过softmax使得他们的范围都在[0,1]内并且和为1:
具体怎么操作呢,以生成ASFF-3为例,Level1是高层语义特征图,比Level3的低层语义特征图相比,分辨率是其四分之一,并且通道数也不同(Level1为512,Level2为256,Level3为128),所以Level1需要先进行1×1卷积压缩通道数到128×,然后再进行4倍上采样从而变成和Level3相同维度的待融合特征图Level1_resized,同理Level2也需要1×1卷积压缩通道并进行2倍上采样变成Level2_resized,然后 A S F F − 3 = α 3 × L e v e l 1 R e s i z e + β 3 × L e v e l 2 R e s i z e + γ 3 × L e v e l 3 ASFF-3=\alpha_3\times Level1 Resize+\beta_3\times Level2 Resize+\gamma_3\times Level3 ASFF−3=α3×Level1Resize+β3×Level2Resize+γ3×Level3
BiFPN
- 经过作者观察,PAN性能比FPN和NAS-FPN要好,但是需要更多参数和计算成本。(PAN里的每一个特征图不但利用了深层语义信息,还利用了浅层语义信息,FPN只有深层语义信息。NAS-FPN是一种神经网络架构搜索出的方法,为什么说PAN比它好,只能说这东西不具有普适性)
- 作者从PAN出发,移除了只有一个输入的节点,并假定这个只有一个输入的节点对特征融合贡献不大。
- 在相同level层添加一个skip connection,为了能融合更多的特征信息。
- 以一个自顶向下和一个自低向上的连法作为一个基础层,不断重复这个模块,就形成了BiFPN特征融合模块。
最后来一个EfficientDet的整体架构图:
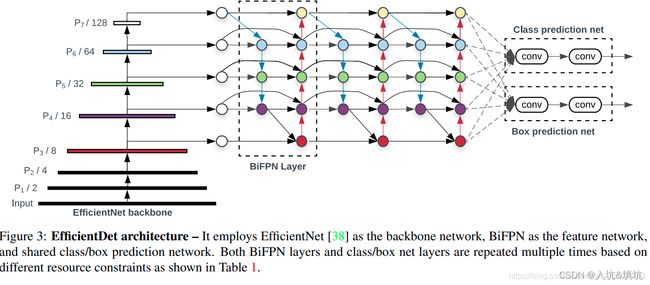
最后进行融合相同尺度特征图的时候采用了ASFF的方法(就是上面那个),让网络自适应学习特征的权重。
激活函数
ReLU
https://blog.csdn.net/weixin_39994739/article/details/122864848
LReLU
LReLU:Leaky-ReLU
L R e L U ( x i ) = { x i , if x i > 0 α i x i , if x i ≤ 0 LReLU(x_i)=\begin{cases} x_i, & \text{if $x_i>0$ } \\ \alpha_i x_i, & \text{if $x_i\leq 0$ } \\ \end{cases} LReLU(xi)={xi,αixi,if xi>0 if xi≤0
α i \alpha_i αi是固定的值
LReLU主要是为了缓解ReLU神经元坏死的问题,缺点是有了负数的输出,导致其非线性程度没有RELU强大,在一些分类任务中效果还没有Sigmoid好。
PReLU
P R e L U ( x i ) = { x i , if x i > 0 α i x i , if x i ≤ 0 PReLU(x_i)=\begin{cases} x_i, & \text{if $x_i>0$ } \\ \alpha_i x_i, & \text{if $x_i\leq 0$ } \\ \end{cases} PReLU(xi)={xi,αixi,if xi>0 if xi≤0
α i \alpha_i αi是一个课更新的非固定的参数
优点:
- PReLU通过增加极少量的参数解决ReLU神经元坏死的问题,并且由于增加的参数量极少,所以网络的计算量以及过拟合的危险性只增加了一点点。特别的,当不同channels使用相同的ai时,参数就更少了。
- BP更新 α i \alpha_i αi时,采用的是带动量的更新方式: Δ α i : = μ Δ α i + ϵ ∂ ϵ ∂ α i \Delta\alpha_i:=\mu\Delta\alpha_i+\epsilon\frac{\partial\epsilon}{\partial\alpha_i} Δαi:=μΔαi+ϵ∂αi∂ϵ
需要特别注意的是:更新 α i \alpha_i αi时不施加权重衰减(L2正则化),因为这会把 α i \alpha_i αi很大程度上push到0。事实上,即使不加正则化,试验中ai也很少有超过1的。
整个论文,ai被初始化为0.25。
ReLU6
R e L U 6 ( x ) = m i n ( m a x ( 0 , x ) , 6 ) ReLU6(x)=min(max(0,x),6) ReLU6(x)=min(max(0,x),6)

ReLU6要是为了在移动端float16的低精度的时候,也能有很好的数值分辨率,如果对ReLu的输出值不加限制,那么输出范围就是0到正无穷,而低精度的float16无法精确描述其数值,带来精度损失
SELU
S E L U ( x ) = λ { x , if x > 0 α ( e x − 1 ) , if x ≤ 0 SELU(x)=\lambda\begin{cases} x, & \text{if $x>0$ } \\ \alpha(e^x-1), & \text{if $x\leq 0$ } \\ \end{cases} SELU(x)=λ{x,α(ex−1),if x>0 if x≤0
S E L U ′ ( x ) = λ { 1 , if x > 0 S E L U ( x ) + α , if x ≤ 0 SELU'(x)=\lambda\begin{cases} 1, & \text{if $x>0$ } \\ SELU(x)+\alpha, & \text{if $x\leq 0$ } \\ \end{cases} SELU′(x)=λ{1,SELU(x)+α,if x>0 if x≤0

在论文中,作者提到SELU可以使得输入在经过一定层数之后变为固定的分布。
以前的ReLU、P-ReLU、ELU等激活函数都是在负半轴坡度平缓,这样在激活的方差过大时可以让梯度减小,防止了梯度爆炸,但是在正半轴其梯度简单的设置为了1。而SELU的正半轴大于1,在方差过小的时候可以让它增大,但是同时防止了梯度消失。这样激活函数就有了一个不动点,网络深了之后每一层的输出都是均值为0,方差为1.
Swish
https://blog.csdn.net/weixin_39994739/article/details/122864848
Hard Swish
h − S w i s h ( x ) = x R e L U 6 ( x + 3 ) 6 h-Swish(x)=x\frac{ReLU6(x+3)}{6} h−Swish(x)=x6ReLU6(x+3)

hard-swish与swish的导数对比图:
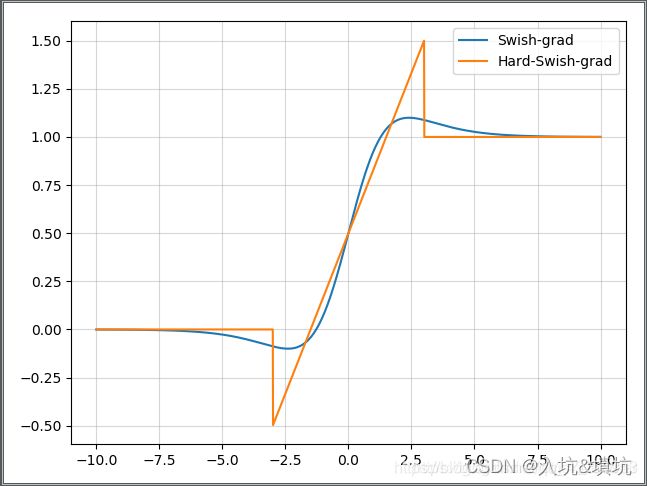
Swish在深层网络中的表现比ReLU好,但计算成本大,使用hard-swish替换swish可以降低计算成本,适合移动端
Mish
f ( x ) = x ∗ t a n h ( l n ( 1 + e x ) ) f(x)=x*tanh(ln(1+e^x)) f(x)=x∗tanh(ln(1+ex))

Mish和Swish导数的对比图
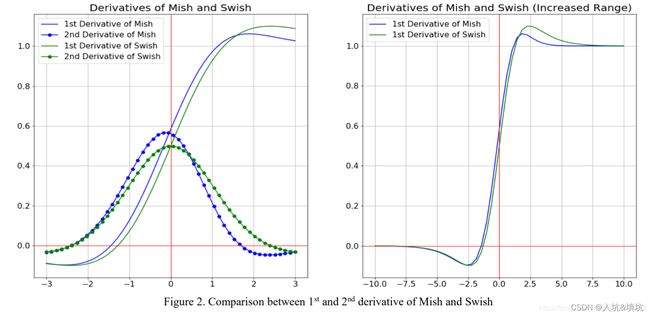
Mish解决了ReLU神经元坏死的问题。理论上轻微的负值能使梯度流更好的传递。但没有理论上对Mish优于Swish的证明,从论文里的实验得出了性能是Mish>Siwhs>ReLU,但计算时间上是ReLU>Swish>Mish(不过Mish比ReLU多的时间不多,一般条件允许的话还是选Mish,不允许就只能选ReLU)
后处理方法——NMS
gredy NMS
gredy NMS为
流程:

在多种目标的情况下,当IoU大于阈值时还要判断是否同一种类别,要是不同类别也放到保留框里。
缺点:
- 顺序处理的模式,计算IoU拖累了运算效率。
- 剔除机制太严格,依据NMS阈值暴力剔除。
- 阈值是经验选取的。
- 评判标准是IoU,即只考虑两个框的重叠面积,这对描述box重叠关系或许不够全面。
Soft NMS
主要旨在缓解Traditional NMS的第二条缺点。
数学上看,Traditional NMS的剔除机制可视为
s i = { 0 , if I o U ( M , B i ) ≥ t h r e s h s i , if I o U ( M , B i ) < t h r e s h s_i=\begin{cases} 0, & \text{if $IoU(M,B_i)\geq thresh$ } \\ s_i, & \text{if $IoU(M,B_i)< thresh$ } \\ \end{cases} si={0,si,if IoU(M,Bi)≥thresh if IoU(M,Bi)<thresh
显然,对于IoU≥NMS阈值的相邻框,Traditional NMS的做法是将其得分暴力置0。这对于有遮挡的案例较不友好。因此Soft-NMS的做法是采取得分惩罚机制,使用一个与IoU正相关的惩罚函数对得分 s s s进行惩罚。
线性NMS
线性惩罚:
s i = { s i ( 1 − I o U ( M , B i ) ) , if I o U ( M , B i ) ≥ t h r e s h s i , if I o U ( M , B i ) < t h r e s h s_i=\begin{cases} s_i(1-IoU(M,B_i)), & \text{if $IoU(M,B_i)\geq thresh$ } \\ s_i, & \text{if $IoU(M,B_i)< thresh$ } \\ \end{cases} si={si(1−IoU(M,Bi)),si,if IoU(M,Bi)≥thresh if IoU(M,Bi)<thresh
其中 M M M代表当前的最大得分框。
缺点:存在不光滑的地方。
高斯NMS
s i = s i e − i o u ( M , b i ) 2 σ s_i=s_ie^{-\frac{iou(M,b_i)^2}{\sigma}} si=sie−σiou(M,bi)2
在迭代终止之后,Soft-NMS依据预先设定的得分阈值来保留幸存的检测框,通常设为0.0001
缺点
- 仍然是顺序处理的模式,运算效率比Traditional NMS更低。
- 对双阶段算法友好,而在一些单阶段算法上可能失效。
- 如果存在定位与得分不一致的情况,则可能导致定位好而得分低的框比定位差得分高的框惩罚更多(遮挡情况下)。
- 评判标准是IoU,即只考虑两个框的重叠面积,这对描述box重叠关系或许不够全面。
DIOU NMS
和原始的NMS不同,DIoU-NMS不仅考虑了IoU的值,还考虑了两个Box中心点之间的距离,使用了新的公式决定一个Box是否被删除:
s i = { s i , if I o U − R D I o U ( M , B i ) < ϵ 0 , if I o U − R D I o U ( M , B i ) ≥ ϵ s_i=\begin{cases} s_i, & \text{if $IoU-R_{DIoU(M,B_i)}<\epsilon$ } \\ 0, & \text{if $IoU-R_{DIoU(M,B_i)}\geq\epsilon$ } \\ \end{cases} si={si,0,if IoU−RDIoU(M,Bi)<ϵ if IoU−RDIoU(M,Bi)≥ϵ
其中,RDIoU是两个Box中心点之间的距离,用下面的公式表示:
R D I o U ( M , B i ) = ρ 2 ( b , b g t ) c 2 R_{DIoU(M,B_i)}=\frac{\rho^2(b,b^{gt})}{c^2} RDIoU(M,Bi)=c2ρ2(b,bgt)
其中 ρ ( ⋅ ) \rho(\cdot) ρ(⋅)是距离, b b b和 b g t b^{gt} bgt表示两个box, c c c是包含两个box的最小box的对角线长度,如下图所示:
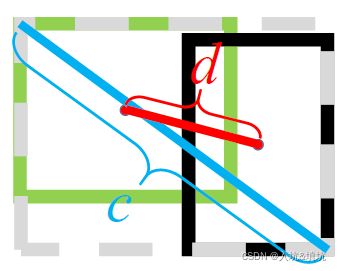
而在实际操作中,研究者还引入了参数 β \beta β,用于控制 d 2 c 2 \frac{d^2}{c^2} c2d2( ρ ( b , b g t ) = d \rho(b,b^{gt})=d ρ(b,bgt)=d)的惩罚幅度。即: D I o U = I o U − ( d 2 c 2 ) β DIoU=IoU-(\frac{d^2}{c^2})^\beta DIoU=IoU−(c2d2)β
优点:
- 从几何直观的角度,将中心点考虑进来有助于缓解遮挡案例。
- 可以与前述NMS变体结合使用。
- 保持NMS阈值不变的情况下,必然能够获得更高recall (因为保留的框增多了),至于precision就需要调 β \beta β来平衡了。
- 个人认为+中心点距离的后处理可以与DIoU/CIoU损失结合使用,这两个损失一方面优化IoU,一方面指引中心点的学习,而中心点距离学得越好,应该对这种后处理思想的执行越有利。

