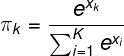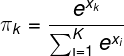【一文学会】Gumbel-Softmax的采样技巧

目录

基于softmax的采样

基于gumbel-max的采样

基于gumbel-softmax的采样

基于ST-gumbel-softmax的采样

Gumbel分布

回答问题一

回答问题二

回答问题三

附录

---

 

以强化学习为例，假设网络输出的三维向量代表三个动作（前进、停留、后退）在下一步的收益，value=[-10,10,15]，那么下一步我们就会选择收益最大的动作（后退）继续执行，于是输出动作[0,0,1]。选择值最大的作为输出动作，这样做本身没问题，但是在网络中这种取法有个问题是不能计算梯度，也就不能更新网络。

基于softmax的采样

这时通常的做法是加上softmax函数，把向量归一化，这样既能计算梯度，同时值的大小还能表示概率的含义（多项分布）。

                                                    

于是value=[-10,10,15]通过softmax函数后有σ(value)=[0,0.007,0.993]，这样做不会改变动作或者说类别的选取，同时softmax倾向于让最大值的概率显著大于其他值，比如这里15和10经过softmax放缩之后变成了0.993和0.007，这有利于把网络训成一个one-hot输出的形式，这种方式在分类问题中是常用方法。

但这样就不会体现概率的含义了，因为σ(value)=[0,0.007,0.993]与σ(value)=[0.3,0.2,0.5]在类别选取的结果看来没有任何差别，都是选择第三个类别，但是从概率意义上讲差别是巨大的。

很直接的方法是依概率采样完事了，比如直接用np.random.choice函数依照概率生成样本值，这样概率就有意义了。所以，经典的采样方法就是用softmax函数加上轮盘赌方法（np.random.choice）。但这样还是会有个问题，这种方式怎么计算梯度？不能计算梯度怎么更新网络？

def sample_with_softmax(logits, size):
# logits为输入数据
# size为采样数
    pro = softmax(logits)
    return np.random.choice(len(logits), size, p=pro)

 

基于gumbel-max的采样

gumbel分布的具体介绍会放在后文，我们先看看结论。对于K维概率向量,对对应的离散变量添加Gumbel噪声，再取样

                                   

其中，是独立同分布的标准Gumbel分布的随机变量，标准Gumbel分布的CDF为.所以可以通过Gumbel分布求逆从均匀分布生成，即。代入计算可知，这里的就是上面softmax采样的，这样就得到了基于gumbel-max的采样过程：

• 对于网络输出的一个K维向量v,生成K个服从均匀分布U(0,1)的独立样本ϵ1,...,ϵK;

• 通过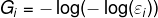计算得到;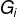

• 对应相加得到新的值向量v′=[v1+G1,v2+G2,...,vK+GK]；

• 取最大值作为最终的类别

可以证明，gumbel-max 方法的采样效果等效于基于 softmax 的方式(后文也会证明)。由于 Gumbel 随机数可以预先计算好，采样过程也不需要计算 softmax，因此，某些情况下，gumbel-max 方法相比于 softmax，在采样速度上会有优势。当然，可以看到由于这中间有一个argmax操作，这是不可导的，依旧没法用于计算网络梯度。

def sample_with_gumbel_noise(logits, size):
    noise = sample_gumbel((size, len(logits)))    # 产生gumbel noise
    return np.argmax(logits + noise, axis=1)

 

基于gumbel-softmax的采样

如果仅仅是提供一种常规 softmax 采样的替代方案， gumbel 分布似乎应用价值并不大。幸运的是，我们可以利用 gumbel 实现多项分布采样的 reparameterization（再参数化）。

在VAE中，假设隐变量（latent variables）服从标准正态分布。而现在，利用 gumbel-softmax 技巧，我们可以将隐变量建模为服从离散的多项分布。在前面的两种方法中，random.choice和argmax注定了这两种方法不可导，但我们可以将后一种方法中的argmax soft化，变为softmax。

                              

temperature 是在大于零的参数，它控制着 softmax 的 soft 程度。温度越高，生成的分布越平滑；温度越低，生成的分布越接近离散的 one-hot 分布。训练中，可以通过逐渐降低温度，以逐步逼近真实的离散分布。

这样就得到了基于gumbel-max的采样过程：

• 对于网络输出的一个K维向量v,生成K个服从均匀分布U(0,1)的独立样本ϵ1,...,ϵK;

• 通过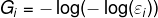计算得到;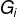

• 对应相加得到新的值向量v′=[v1+G1,v2+G2,...,vK+GK]；

• 通过softmax函数计算概率大小得到最终的类别。

def differentiable_gumble_sample(logits, temperature=1):
    noise = tf.random_uniform(tf.shape(logits), seed=11)
    logits_with_noise = logits - tf.log(-tf.log(noise))
    return tf.nn.softmax(logits_with_noise / temperature)

 

基于ST-gumbel-softmax的采样

temperature >0时，用gumbel-softmax的采样不会完全遵循范畴分布（单次的多项分布）。可以考虑前向传递时用gumbel-max的离散值，反向传递时用gumbel-softmax的连续值，实现过程可见Jang的paper。

 

---

OK，到此就是介绍了不同的采样方法。我们再回头看看还有哪些问题没有讲清楚：

1、为什么方法三能生成和方法一一样的效果？

2、为什么使用Gumbel分布就可以逼近多项分布采样？（这一部分我们会有理论证明）

3、为什么 用了reparameterization（再参数化）就是可导的？

 

Gumbel分布

首先，我们介绍一样何为gumbel分布，gumbel分布是一种极值型分布。举例而言，假设一天内每次的喝水量为一个随机变量，它可能服从某个概率分布，记下这一天内喝的10次水的量并取最大的一个作为当天的喝水量值。显然，每天的喝水量值也是一个随机变量，并且它的概率分布即为 Gumbel 分布。实际上，只要是指数族分布，它的极值分布都服从Gumbel分布。

它的概率密度函数（PDF）长这样：

                                   

公式中， 是位置系数（Gumbel 分布的众数是 ）， 是尺度系数（Gumbel 分布的方差是 ）。

转存失败重新上传取消

 

def gumbel_pdf(x, mu=0, beta=1):
    z = (x - mu) / beta
    return np.exp(-z - np.exp(-z)) / beta

 

回答问题一

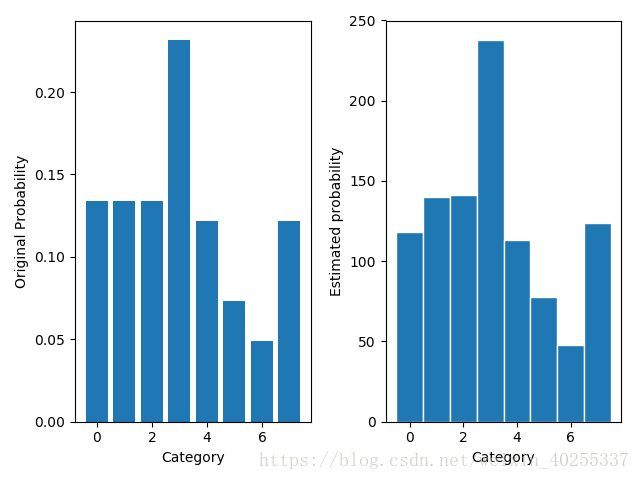
先定义一个多项分布，作出真实的概率密度图。再通过采样的方式比较各种方法的效果。这里定义了一个8类别的多项分布，其真实的密度函数如下左图。

首先我们直接根据真实的分布利用np.random.choice函数采样对比效果（实现代码放在文末）

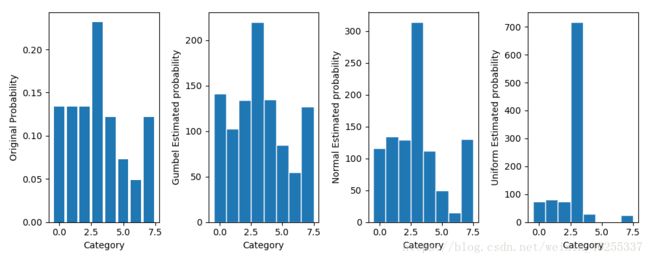
左图为真实概率分布，右图为采用np.random.choice函数采样的结果（采样次数为1000）。可见效果还是非常好的，要是没有不能求梯度这个问题，直接从原分布采样是再好不过的。接着通过前述的方法添加Gumbel噪声采样，同时也添加正态分布和均匀分布的噪声作对比。（基于gumbel-max的采样）

可以明显看到Gumbel噪声的采样效果是最好的，正态分布其次，均匀分布最差。也就是说用Gumbel分布的样本点最接近真实分布的样本。

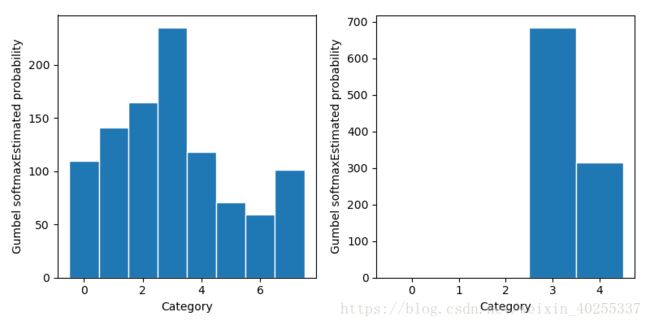
最后，我们基于gumbel-softmax做采样，左图设置temperature=0.1，经过softmax函数后得到的概率分布接近one-hot分布，用此概率分布对分类求期望值，得到结果为左图，可以较好地逼近方法一的采样结果；右图设置temperature=5，经过softmax函数后得到的概率分布接近均匀分布，再对分类求期望值，得到的结果集中在类别3、 4（中间的类别）。这和gumbel-softmax具备的性质是一致的，temperature控制着softmax的soft程度，温度越高，生成的分布越平滑（接近这里的均匀分布）；温度越低，生成的分布越接近离散的one-hot分布。因此，训练时可以逐渐降低温度，以逐步逼近真实的离散分布。（基于gumbel-softmax的采样）

到此为此，我们也算用一组实验去解释了为什么方法二、方法三时可行的。具体的代码放在文末了，感兴趣的可以研究一下。

 

回答问题二

为什么它可以有这样的效果？为什么添加gumbel噪声就可以近似范畴分布（category distribution）采样。

我们来考虑一个问题，假设一共有K个类别，那么第k个类别恰好是最大的概率是多少？

对于一个K维的输出向量，每个维度的值记为,通过softmax函数可得，取到每个维度的概率为：

                                                 

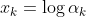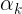设，可以看出即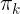，这是直接用softmax得到的概率密度函数，它也可以换一种方式去说，对每个添加独立的标准Gumbel分布(尺度参数为1，位置参数为0)噪声，并选择值最大的维度作为输出，得到的概率密度同样为。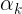

我们现在来证明这事。

回顾一下刚刚说的gumbel分布。尺度参数为1，位置参数为的gumbel分布的PDF为：

                                                      

以及CDF为：

                                                      

假设对应,相加得到随机变量,这就相当于服从尺度参数为1，位置参数为的Gumbel分布。要证明取到第k个位置的概率为，首先计算比其他大的概率。

          

现在我们有了是最大的那个概率值，现在我们想知道第k个元素是最大的概率值是多少，因此，我们需要对所有z的取值进行积分，从而得到第k个位置取值最大的概率。对求积分可得边缘累积概率分布函数 

的概率调用gumbel分布的PDF，即，为最大的概率上面已经证明，带入化简，最后一步积分里面是的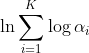的Gumbel分布，所以整个积分为1。于是上面这条等式恰好是一个softmax的公式，也就是说，第k个位置最大的概率，恰好就是对离散概率分布的一个近似。

 

回答问题三

最后，再来回答一样为什么再参数化(reparameterization tricks)就可以变得可导。

reparameterization tricks是什么

reparameterization tricks的思想是说如果我们能把一个复杂变量用一个标准变量来表示，比如   ，其中 ϵ∼N(0;1) ，那么我们就可以用ϵ这个变量取代z。举个例子，假如p(z;θ)是个复杂分布，现在我们想将z再参数化，用p(ϵ)去表示p(z;θ)，即ϵ∼N(0;1)，用一个one-liners（简单理解为一行变换，g(ϵ;θ)）表示从ϵ到z的联系，令g(ϵ;θ)为μ+Rϵ。

这样做是有好处的，一方面在更新梯度时可以将随机变量提取出来，不影响对参数的更新（如上图中的μ，R）；另一方面假如我们要依据p(z;θ)采样，然后再利用采样处的梯度修正p，这样两次的误差就会叠加，但现在只需要从一个分布非常稳定的random seed的分布中采样，比如N(0,1)所以noise小得多。常见的变换方法可见此文。实际运用起来就是，

                         

我们现在将reparameterization tricks应用到采样中。原本，网络中参数包括前向传递和反向传递（如下图左半部分），现在我们计算出P(Z)后，依概率采样（np.random.choice），由P(Z)得到样本z没问题，但反向传递时如何找到并更新P(Z)就没法办了。

转存失败重新上传取消

然后，再参数化就可以解决这个问题。我们令，在上面的证明中，已经证明了使用随机变量去采样是正确的，现在我们重新观察此式，服从gumbel分布不正是可以看成基分布（base distribution）p(ϵ)嘛！令g(ϵ;θ)为，所以从中采样就变为从中采样，而我们在更新时可以避开简单随机变量，只更新参数。

转存失败重新上传取消

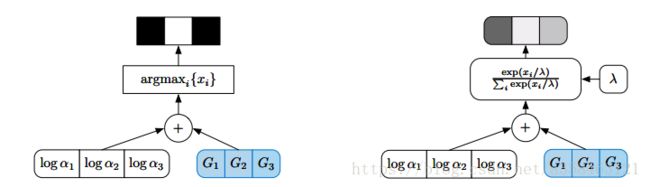
最后，放上用gumbel-max和gumbel-softmax采样的图结构。（图中改成）图底下的“+”号可以看到，这是一种重参数的方法，通过加一个随机的，固定分布的噪声，从而实现采样。

 

附录

放上代码：

from scipy.optimize import curve_fit
import numpy as np
import matplotlib.pyplot as plt

n_cats = 8
n_samples = 1000
cats = np.arange(n_cats)
probs = np.random.randint(low=1, high=20, size=n_cats)
probs = probs / sum(probs)
logits = np.log(probs)

def plot_probs():   # 真实概率分布
    plt.bar(cats, probs)
    plt.xlabel("Category")
    plt.ylabel("Original Probability")

def plot_estimated_probs(samples,ylabel=''):
    n_cats = np.max(samples)+1
    estd_probs,_,_ = plt.hist(samples,bins=np.arange(n_cats+1),align='left',edgecolor='white')
    plt.xlabel('Category')
    plt.ylabel(ylabel+'Estimated probability')
    return estd_probs

def print_probs(probs):
    print(probs)

samples = np.random.choice(cats,p=probs,size=n_samples) # 依概率采样

plt.figure()
plt.subplot(1,2,1)
plot_probs()
plt.subplot(1,2,2)
estd_probs = plot_estimated_probs(samples)
plt.tight_layout() # 紧凑显示图片
plt.savefig('/home/zhumingchao/PycharmProjects/matplot/gumbel1')

print('Original probabilities:\t',end='')
print_probs(probs)
print('Estimated probabilities:\t',end='')
print_probs(estd_probs)
plt.show()
######################################

def sample_gumbel(logits):
    noise = np.random.gumbel(size=len(logits))
    sample = np.argmax(logits+noise)
    return sample
gumbel_samples = [sample_gumbel(logits) for _ in range(n_samples)]

def sample_uniform(logits):
    noise = np.random.uniform(size=len(logits))
    sample = np.argmax(logits+noise)
    return sample
uniform_samples = [sample_uniform(logits) for _ in range(n_samples)]

def sample_normal(logits):
    noise = np.random.normal(size=len(logits))
    sample = np.argmax(logits+noise)
    # print('old',sample)
    return sample
normal_samples = [sample_normal(logits) for _ in range(n_samples)]

plt.figure(figsize=(10,4))
plt.subplot(1,4,1)
plot_probs()
plt.subplot(1,4,2)
gumbel_estd_probs = plot_estimated_probs(gumbel_samples,'Gumbel ')
plt.subplot(1,4,3)
normal_estd_probs = plot_estimated_probs(normal_samples,'Normal ')
plt.subplot(1,4,4)
uniform_estd_probs = plot_estimated_probs(uniform_samples,'Uniform ')
plt.tight_layout()
plt.savefig('/home/zhumingchao/PycharmProjects/matplot/gumbel2')

print('Original probabilities:\t',end='')
print_probs(probs)
print('Gumbel Estimated probabilities:\t',end='')
print_probs(gumbel_estd_probs)
print('Normal Estimated probabilities:\t',end='')
print_probs(normal_estd_probs)
print('Uniform Estimated probabilities:\t',end='')
print_probs(uniform_estd_probs)
plt.show()
#######################################

def softmax(logits):
    return np.exp(logits)/np.sum(np.exp(logits))

def differentiable_sample_1(logits, cats_range, temperature=.1):
    noise = np.random.gumbel(size=len(logits))
    logits_with_noise = softmax((logits+noise)/temperature)
    # print(logits_with_noise)
    sample = np.sum(logits_with_noise*cats_range)
    return sample
differentiable_samples_1 = [differentiable_sample_1(logits,np.arange(n_cats)) for _ in range(n_samples)]

def differentiable_sample_2(logits, cats_range, temperature=5):
    noise = np.random.gumbel(size=len(logits))
    logits_with_noise = softmax((logits+noise)/temperature)
    # print(logits_with_noise)
    sample = np.sum(logits_with_noise*cats_range)
    return sample
differentiable_samples_2 = [differentiable_sample_2(logits,np.arange(n_cats)) for _ in range(n_samples)]

def plot_estimated_probs_(samples,ylabel=''):
    samples = np.rint(samples)
    n_cats = np.max(samples)+1
    estd_probs,_,_ = plt.hist(samples,bins=np.arange(n_cats+1),align='left',edgecolor='white')
    plt.xlabel('Category')
    plt.ylabel(ylabel+'Estimated probability')
    return estd_probs

plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
gumbelsoft_estd_probs_1 = plot_estimated_probs_(differentiable_samples_1,'Gumbel softmax')
plt.subplot(1,2,2)
gumbelsoft_estd_probs_2 = plot_estimated_probs_(differentiable_samples_2,'Gumbel softmax')
plt.tight_layout()
plt.savefig('/home/zhumingchao/PycharmProjects/matplot/gumbel3')

print('Gumbel Softmax Estimated probabilities:\t',end='')
print_probs(gumbelsoft_estd_probs_1)
plt.show()

我是小明，如果对文章内容或者其他想一起探讨的，欢迎前来。

 

本篇文章参考了以下：

http://www.cnblogs.com/initial-h/p/9468974.html

https://blog.csdn.net/jackytintin/article/details/79364490

https://blog.csdn.net/a358463121/article/details/80820878

https://arxiv.org/pdf/1611.01144.pdf

http://blog.shakirm.com/2015/10/machine-learning-trick-of-the-day-4-reparameterisation-tricks/

https://arxiv.org/pdf/1308.3432.pdf