BP神经网络公式推导（含代码实现）

什么是BP神经网络

BP（Back Propagation）神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差最小。

BP神经网络包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。

网络结构：BP神经网络整个网络结构包含了：一层输入层，一到多层隐含层，一层的输出层。

隐含层的选取

在BP神经网络中，输入层和输出层的节点个数都是确定的，而隐含层节点个数不确定，那么应该设置为多少才合适呢？实际上，隐含层的节点个数的多少对神经网络的性能是有影响的，有一个经验公式可以确定隐含层节点数目，公式如下：
$$h=\sqrt{m+n}+a$$
其中h为隐含层节点数目，m为输入层节点数目，n为输出层节点数目，a为1~10之间的调节常数。

单神经元梯度

信号的前向传播

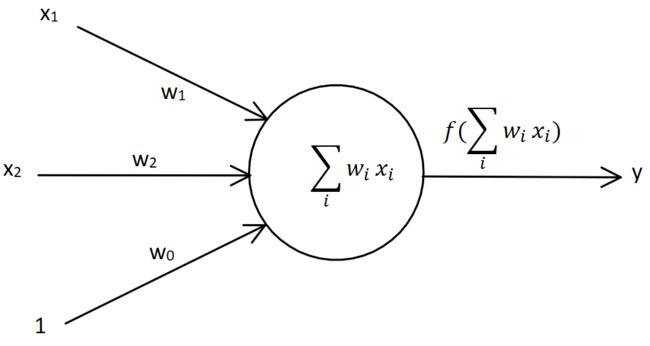
为了便于理解，这里先用单个神经元梯度为例。

图中有两个输入$[x_1,x_2]$，两个权值$[w_1,w_2]$，偏置值为$w_0$，f为激活函数。

前向传播过程中：
$$\begin{gathered} z=w_0{x}_0+w_1{x}_1+w_2{x}_2=\sum _{i=0}^2{w}_i{x}_i,其中x_0=1 \\ y=f\sum _{i=0}^2{w}_i{x}_i \end{gathered}$$
用向量形式可表示为：
$$\begin{gathered} z=\sum _{i=0}^2{w}_i{x}_i=w^{T}x \\ y=f(w^{T}x) \end{gathered}$$

误差的反向传播

在BP神经网络中，误差反向传播基于Delta学习规则。我们已知输出层的结果为$y=y=f(w^{T}x)$，对于预测值与真实值之间误差的计算，我们使用如下公式（代价函数）：
$$E=\frac{1}{2}(t-y{)}^2$$
其中真实值为t。

BP神经网络的主要目的是修正权值，使得误差数值达到最小。Delta学习规则是一种利用梯度下降的一般性的学习规则。公式如下：
$$\begin{array}{rl}\Delta W& =-ŋE^{\prime }\\ \frac{\delta E}{\delta w}& =\frac{\delta \frac{1}{2}[t-f(w^{T}x){]}^2}{\delta w}\\ & =\frac{1}{2}\ast 2[t-f(w^{T}x)]\ast (-f^{\prime }(w^{T}x))\frac{\delta w^{T}x}{\delta w}\\ & =-(t-y)f^{\prime }(w^{T}x)x\\ \Delta W& =-ŋE^{\prime }=ŋ(t-y)f^{\prime }(w^{T}x)x=ŋ\delta x,其中\delta =(t-y)f^{\prime }(w^{T}x)\end{array}$$

Delta学习规则小结

全连接层梯度

正向传播

第一层

输入$x_1,x_2,x_3$

$$\begin{gathered} h_1^1=u_{11}{x}_1+u_{21}{x}_2+u_{31}{x}_3=\sum _{i=1}^3{u}_{i1}{x}_i \\ {h}_2^1=u_{12}{x}_1+u_{22}{x}_2+u_{32}{x}_3=\sum _{i=1}^3{u}_{i2}{x}_i \\ {H}_1^1=f(h_1^1) \\ {H}_2^1=f(h_2^1) \\ {h}^1=[h_1^1,h_2^1]={\left[\begin{array}{ccc}{u}_{11}& u_{21}& u_{31}\\ u_{12}& u_{22}& u_{32}\end{array}\right]}^T\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=u^{T}x \\ {H}^1=f(u^{T}x) \end{gathered}$$
上图有两个隐含层，为了便于解释，这里用$x_i^j$表示第j层的第i个节点，如$h_1^1$表示第一个隐含层的第一个节点。

第二层

输入$H_1^1,H{2}^1$
$$\begin{gathered} h_1^2=w_{11}{H}_1^1+w_{21}{H}_2^1 \\ {h}_2^2=w_{12}{H}_1^1+w_{22}{H}_2^1 \\ {H}_1^2=f(h_1^2) \\ {h}_2^2=f(h_2^2) \\ {h}^2=[h_1^2,h_2^2]={\left[\begin{array}{cc}{w}_{11}& w_{21}\\ w_{12}& w_{22}\end{array}\right]}^T\left[\begin{array}{c}{H}_1^1\\ H_2^1\end{array}\right]=w^T{H}^1 \\ {H}^2=f(w^T{H}^1) \end{gathered}$$
输出层

输入$H_1^2,h_2^2$
$$y=f(v_1{H}_1^2+v_2{H}_2^2)=f(v^T{H}^2)$$

反向传播

输出层
$$\begin{array}{rl}\Delta W& =-ŋE^{\prime }=ŋ(t-y)f^{\prime }(v^T{H}^2)H^2=ŋ\delta H^2\\ \delta & =(t-y)f^{\prime }(v^T{H}^2)\end{array}$$
第二层

首先根据Delta学习规则可得：
$$\begin{array}{rl}\Delta W& =-ŋE^{\prime }\\ \frac{\delta E}{\delta w}& =\frac{\delta \frac{1}{2}[t-f(v^T{H}^2){]}^2}{\delta w}\\ & =\frac{1}{2}\ast 2[t-f(v^T{H}^2)]\ast (-f^{\prime }(v^T{H}^2))\frac{\delta v^T{H}^2}{\delta w}\\ & =-(t-y)f^{\prime }(v^T{H}^2)\frac{\delta v^T{H}^2}{\delta w}\end{array}$$
此时我们先计算$\frac{\delta v^T{H}^2}{\delta w}$的取值：
$$\begin{array}{rl}\frac{\delta v^T{H}^2}{\delta w}& =\frac{\delta v^T{H}^2}{\delta H^2}\ast \frac{\delta H^2}{\delta w}\\ & =v^T\frac{\delta f(w^T{H}^1)}{\delta w}\\ & =v^T{f}^{\prime }(W^T{H}^1)H^1\end{array}$$
这样我们就可以将上述结果带入到$\Delta W$中
$$\begin{array}{rl}\Delta W& =ŋ(t-y)f^{\prime }(v^T{H}^2)\frac{\delta v^T{H}^2}{\delta w}\\ & =ŋ(t-y)f^{\prime }(v^T{H}^2)v^T{f}^{\prime }(W^T{H}^1)H^1\\ & =ŋ\delta v^T{f}^{\prime }(W^T{H}^1)H^1\\ & =ŋ{\delta }^2{H}^1\end{array}$$
最后我们就得到了${\delta }^2$
$${\delta }^2=\delta v^T{f}^{\prime }(W^T{H}^1)$$
第一层

首先根据Delta学习规则可得：
$$\begin{array}{rl}\Delta W& =-ŋE^{\prime }\\ \frac{\delta E}{\delta u}& =\frac{\delta \frac{1}{2}[t-f(v^T{H}^2){]}^2}{\delta u}\\ & =\frac{1}{2}\ast 2[t-f(v^T{H}^2)]\ast (-f^{\prime }(v^T{H}^2))\frac{\delta v^T{H}^2}{\delta u}\\ & =-(t-y)f^{\prime }(v^T{H}^2)\frac{\delta v^T{H}^2}{\delta u}\end{array}$$

此时我们先计算$\frac{\delta v^T{H}^2}{\delta u}$的取值：
$$\begin{array}{rl}\frac{\delta v^T{H}^2}{\delta u}& =\frac{\delta v^T{H}^2}{\delta H^2}\ast \frac{\delta H^2}{\delta H^1}\ast \frac{\delta H^1}{\delta u}\\ & =v^T\frac{\delta f(w^T{H}^1)}{\delta H^1}\ast \frac{\delta f(u^{T}x)}{\delta u}\\ & =v^T{f}^{\prime }(w^T{H}^1)w^T\ast f^{\prime }(u^{T}x)x\end{array}$$
这样我们就可以将上述结果带入到$\Delta W$中
$$\begin{array}{rl}\Delta W& =ŋ(t-y)f^{\prime }(v^T{H}^2)\frac{\delta v^T{H}^2}{\delta u}\\ & =ŋ(t-y)f^{\prime }(v^T{H}^2)v^T{f}^{\prime }(w^T{H}^1)w^T\ast f^{\prime }(u^{T}x)x\\ & =ŋ\delta v^T{f}^{\prime }(w^T{H}^1)w^T\ast f^{\prime }(u^{T}x)x\\ & =ŋ{\delta }^2{w}^T{f}^{\prime }(u^{T}x)x\\ & =ŋ{\delta }^{1}x\end{array}$$
参考
$$\begin{gathered} \delta =(t-y)f^{\prime }(v^T{H}^2) \\ {\delta }^2=\delta v^T{f}^{\prime }(W^T{H}^1) \end{gathered}$$
最后我们就得到了${\delta }^1$
$${\delta }^1={\delta }^2{w}^T{f}^{\prime }(u^{T}x)$$

代码

import numpy as np

#输入数据
X = np.array([[1,0,0],
              [1,0,1],
              [1,1,0],
              [1,1,1]])
#标签
Y = np.array([[0,1,1,0]])
#权值初始化，取值范围-1到1
V = np.random.random((3,4))*2-1 
W = np.random.random((4,1))*2-1
print(V)
print(W)
#学习率设置
lr = 0.11

def sigmoid(x):
    return 1/(1+np.exp(-x))

def dsigmoid(x):
    return x*(1-x)

def update():
    global X,Y,W,V,lr
    
    L1 = sigmoid(np.dot(X,V))#隐藏层输出(4,4)
    L2 = sigmoid(np.dot(L1,W))#输出层输出(4,1)
    
    L2_delta = (Y.T - L2)*dsigmoid(L2)
    L1_delta = L2_delta.dot(W.T)*dsigmoid(L1)
    
    W_C = lr*L1.T.dot(L2_delta)
    V_C = lr*X.T.dot(L1_delta)
    
    W = W + W_C
    V = V + V_C
    
for i in range(20000):
    update()#更新权值
    if i%500==0:
        L1 = sigmoid(np.dot(X,V))#隐藏层输出(4,4)
        L2 = sigmoid(np.dot(L1,W))#输出层输出(4,1)
        print('Error:',np.mean(np.abs(Y.T-L2)))
        
L1 = sigmoid(np.dot(X,V))#隐藏层输出(4,4)
L2 = sigmoid(np.dot(L1,W))#输出层输出(4,1)
print(L2)

参考资料：

https://segmentfault.com/a/1190000021529971