深度学习中的激活函数
深度学习中的激活函数
- 1、sigmoid
- 2、softmax
- 3、tanh
- 4 、ReLU
- 5、Leaky ReLU
- 6、PReLU
神经网络用于实现复杂的函数,而非线性激活函数能够使神经网络逼近任意复杂的函数。如果没有激活函数引入的非线性,多层神经网络就相当于单层的神经网络。
一个激活函数应该具有的属性:
1、非线性。
2、几乎处处可微。
3、计算简单。
4、非饱和性。
5、单调性。
6、参数少。
1、sigmoid
公式:
α ( x ) = 1 1 + e ( − x ) , . \alpha(x) = \dfrac{1}{1+e^{(-x)}},. α(x)=1+e(−x)1,.
函数图像如下:

Sigmoid也被称为逻辑激活函数(Logistic Activation Function),就是 Logistic 函数。它将一个实数值压缩到0至1的范围内。当我们的最终目标是预测概率时,它可以被应用到输出层。
Sigmoid函数的优点:
1、处处可导。
2、将函数数值压缩到[0, 1]之间,在网络最后一层加入sigmoid便于我们处理二分类问题。
Sigmoid函数的缺点:
1、梯度消失。sigmoid有激活区与饱和区。sigmoid的梯度在激活区梯度较大,使用梯度下降法可以快速更新参数;而在饱和区时梯度非常小,导致反向传播时参数更新速度慢甚至更新速度为0。
2、求导计算量大。
3、均值不为0,输出大于0时,则梯度方向将大于0,也就是说接下来的反向运算中将会持续正向更新;同理,当输出小于0时,接下来的方向运算将持续负向更新。
早期的神经网络喜欢使用sigmoid用作中间层与最终层的激活函数,但基于上述缺点特别是现在的网络深度做的很深,非常容易产生梯度消失情况,因此现在一般使用RuLU。当 sigmoid用于最终的输出层时,适用于类别非互斥的多分类任务中,sigmoid输出的概率和不一定等于1(例如多标签的分类任务,帅哥可以是man也可以是human,二者不排斥),通常后面接交叉熵作为损失函数。
2、softmax
公式:
σ ( x ) = e x i ∑ j = 1 n e x j \sigma(x) = \dfrac{e^{x_i}}{\sum_{j=1}^ne^{x_j}} σ(x)=∑j=1nexjexi
这里说softmax是因为sigmoid与softmax很像,在二分类的情况下sigmoid与softmax是等价的。sofxmax很少用于中间层的激活函数,但是sigmoid与softmax仅仅是两种不同的激活函数而已,作为中间层的激活函数是为了使网络具有非线性的激活函数使其具有逼近任何函数的能力。softmax作为网络的最后一层有特殊的作用,在输出层后接上softmax使得多项分布的输出在0~1之间,而且和为1,常用于类别独立的多分类任务中,如预测数字或者猫狗。
3、tanh
公式:
t a n h ( x ) = s i n h ( x ) c o s h ( x ) = e x − e − x e x + e − x = 2 s i g m o i d ( 2 x ) − 1 tanh(x) = \dfrac{sinh(x)}{cosh(x)} = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}=2sigmoid(2x) - 1 tanh(x)=cosh(x)sinh(x)=ex+e−xex−e−x=2sigmoid(2x)−1
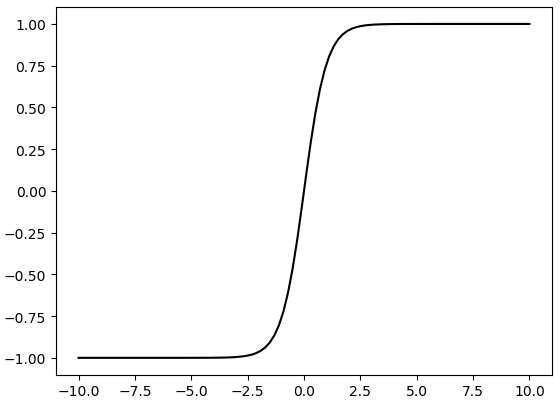
Tanh叫双曲正切激活函数,类似sigmoid能把值压缩,但tanh是把值压缩在-1~1之间,tanh在特征相差明显的时候效果会很好,在循环过程中会不断扩大特征效果。
tanh的优点:
1、处处可导。
2、均值为0。
3、输出和输入能够保持非线性单调上升和下降关系,符合BP网络的梯度求解,容错性好,有界,渐进于0、1,符合人脑神经饱和的规律。
tanh的缺点:
1、梯度消失。
2、计算量大。
tanh常用于RNN中,RNN的每个时间步的权重是相同的,bp过程相当于权重的连续相乘,因此比CNN更容易出现梯度消失和梯度爆炸,因此采用tanh比较多。tanh也会出现梯度消失和梯度爆炸,但是相比于Sigmoid好很多了。理论上ReLU+梯度裁切也可以。
对于为什么CNN用ReLU,RNN用tanh的问题可参考为什么RNN用tanh,与RNN 中为什么要采用 tanh,而不是 ReLU 作为激活函数?
4 、ReLU
公式:
r e l u ( x ) = m a x ( 0. x ) relu(x) =max(0. x) relu(x)=max(0.x)
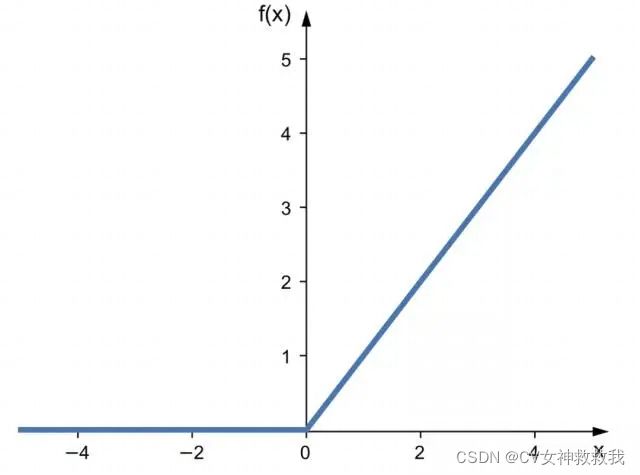
ReLU全称Rectified Linear Units,修正线性单元。是目前图像领域中最常用的中间层。激活函数,当x<0时,ReLU赢饱和,当x>0时,则不存在饱和问题。
ReLU优点:
1、当x>0时保持梯度不衰减,可以缓解梯度消失的问题。
2、简单,速度快。
ReLU缺点:
1、当x<0时,函数位于硬饱和区,导致对应权重无法更新,这种现象叫“神经元死亡”。
2、均值大于0。偏移现象与神经元死亡会共同影响网络哦的收敛性。
5、Leaky ReLU
公式:
f ( x ) = { α x , ( x < 0 ) x , ( x > = 0 ) f(x)=\left\{ \begin{array}{c} \alpha x,(x<0) \\ x,(x>=0)\end{array}\right. f(x)={αx,(x<0)x,(x>=0)
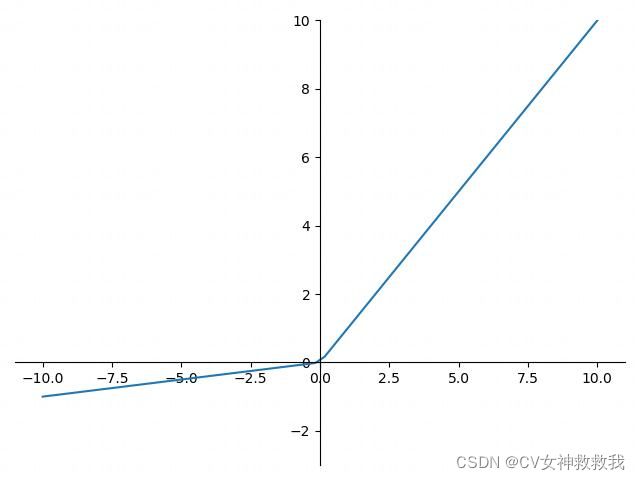
Leaky ReLU是relu的改进版,主要消灭了relu的神经元死亡现象。这个leaky relu通常比relu效果好,但是实际中Leaky ReLU使用的并不多,Leaky ReLU中 α \alpha α为常数。
6、PReLU
公式
f ( x ) = { α x , ( x < 0 ) x , ( x > = 0 ) f(x)=\left\{ \begin{array}{c} \alpha x,(x<0) \\ x,(x>=0)\end{array}\right. f(x)={αx,(x<0)x,(x>=0)
PReLU与Leaky ReLU长的一样,但Leaky ReLU中的 α \alpha α是可以训练的。如果ai是一个很小的固定值(如ai=0.01),则PReLU退化为Leaky ReLU(LReLU)。 有实验证明,与ReLU相比,LReLU对最终的结果几乎没什么影响。 α \alpha α一般初始化为0.25。
常用的激活函数介绍到此,更多激活函数可以参考这里。