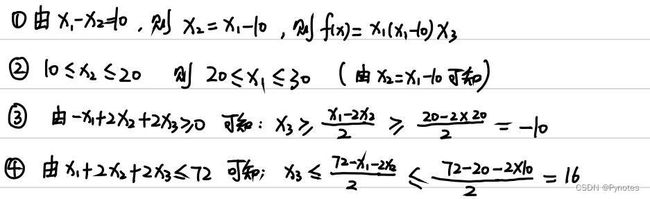Python实现蒙塔卡洛思想

蒙特卡洛

目录

一、buffon 投针试验

法国数学家布丰（buffon）最早设计了投针试验。

步骤：

1）取一张白纸，画许多等间距$（a）$的平行线
2）取长度为 l（l$\le$a）的针，随机投向上述纸张 n 次，并记录针与纸张的相交总次数 m
3）计算针与直线相交的概率
$【结论】：$ $$p=2l/\pi a$$
下图来源于清风数学建模

$【分析】：$

• 分析问题

  • 以 M 表示针的中点，x 表示 M 与最近一条平行线的距离，$\varphi$表示针与此直线的夹角。
  • 示例图（此图来源于网络）

• 数学建模

  • 条件：

    • 0 $\le$ x $\le$ $\frac{a}{2}$

    • 0 $\le$ $\varphi$ $\le$ π

    • x $\le$ $\frac{l}{2}$sin$\varphi$

    • 几何概型
      

    • $$p=\frac{{\int }_0^{\pi }\frac{l}{2}sin\varphi }{\frac{l}{2}a\pi }=\frac{2l}{\pi a}$$

• 仿真

  • 思路和代码如下：

  import numpy as np
  
  
  def buff(l=0.520, a=1.314, n=10000):
    # l = 0.520 # 针长
    # a = 1.314 # 两平行线间距
    # n = 10000 # 投针次数
    m = 0 # 初始相交次数
    x = np.random.rand(1,n)*(a/2) # 产生n个[0, a/2]随机数, 用来表示针中点到最近平行线的距离
    fai = np.random.rand(1,n)*(np.pi) # 产生n个角度值
    for i,j in zip(x[0],fai[0]):
        if i <= (l/2)*np.sin(j):
            m += 1
    p = m/n # 10000次随机试验相交的频率
    m_pi = (2*l)/(a*p)
    print("利用蒙特卡洛方法模拟投针试验得到的pi值：{:.4f}".format(m_pi))
  
  
  buff()
  

二、蒙特卡洛方法概述

• 定义：
  • 蒙特卡洛方法又称统计模拟法，是一种随机模拟方法，基于概率与数理统计的一种计算方法，是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解得问题与一定的概率模型相联系，用计算机来实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡洛命名。
• 提出
  • 20 世纪 40 年代由乌拉姆和冯诺依曼首先提出。1777 年，法国 Buffon 提出用投针试验的方法求圆周率，这被认为是蒙特卡洛方法的起源。
• 原理
  • 大数定理：当试验次数趋向于 ∞ 时，频率就趋向于概率

三、应用实例介绍

• 三门问题

假设张三参加一档电视节目，节目组提供了ABC三扇门，主持人告诉你，只有一门后有辆汽车，其余皆空。
又假如你选择了B门，这时，主持人打开了C门，并让你看到是空的，然后问你要不要改选A门？

• 代码和思路

  import numpy as np
  
  
  n = 100000 # 重复试验的次数
  a = 0 # a表示不改变主意时能赢得汽车的次数
  b = 0 # b表示改变主意时能赢得汽车的次数
  for i in range(1,100001):
      x = np.random.choice([1,2,3]) # 随机生成一个1-3之间的整数x表示汽车出现在第x扇门后
      y = np.random.choice([1,2,3]) # 随机生成一个1-3之间的整数y表示自己选的门
      if x == y:
          a += 1
          b += 0
      else:
          a += 0
          b += 1
  p_no_change = a/(a+b)
  p_change = b/(a+b)
  print("蒙特卡罗方法得到的不改变主意时的获奖概率为：", p_no_change)
  print("蒙特卡罗方法得到的改变主意时的获奖概率为：", p_change)
  

• 模拟排队问题

   假设某银⾏⼯作时间只有⼀个服务窗⼝，⼯作⼈员只能逐个的接待顾客。当来的顾客较多时，⼀部分顾客就需要排队等待。
       假设：
         1) 顾客到来的间隔时间服从参数为0.1的指数分布；
         2) 每个顾客的服务时间服从均值为10，⽅差为4的正态分布(单位为分钟，若服务时间⼩于1分钟，则按1分钟计算)；
         3) 排队按先到先服务的规则，且不限制队伍的⻓度，每天⼯作时⻓为8⼩时。
       试回答下⾯的问题：
         1) 模拟⼀个⼯作⽇，在这个⼯作⽇共接待了多少客户，客户平均等待的时间为多少?
         2) 模拟100个⼯作⽇，计算出平均每⽇接待客户的个数以及每⽇客户的平均等待时⻓。

• 银行排队图（来源于清风数学建模）
  

• 分析：
  

• 数学建模
  

  

• 仿真：

from datetime import datetime
import numpy as np
import time
startTime = datetime.now()
b = [0] # 客户开始被服务的时间序列
c = [0] # 客户到达的时间序列
e = [0] # 客户被服务结束的时间序列
x = [0] # 客户到达时间间隔系列
y = [0] # 客户被服务时间序列
allWaitTime = 0 # 用来表示所有客户等待的总时间，初始化为0
x.append(np.random.exponential(10)) # 第0个客户(假想的)和第1个客户到达的时间间隔
c.append(c[0]+x[1]) # 第一个客户到达的时间
b.append(c[1]) # 第一个客户开始服务的时间
i = 1
while b[i] <= 480:
    y_i = np.random.normal(10,2) # 服务时间
    if y_i < 1:
        y_i = 1
        y.append(y_i)
    else:
        y.append(y_i)
    e.append(b[i] + y[i])
    waitTime = b[i] - c[i]
    allWaitTime = allWaitTime + waitTime # 更新客户总等待时间
    i += 1 # 增加一位新客户
    x.append(np.random.exponential(10)) # 这位新客户和上一个客户到达的时间间隔
    c.append(c[i-1]+x[i]) # 这位新客户到达银行的时间
    b.append(max(c[i], e[i-1])) # 这个新客户开始服务的时间取决于其到达时间和上一个客户结束服务的时间
n = len(c) - 1 # 银行一天8小时一共服务的客户人数
t = allWaitTime / n # 客户的平均等待时间        
print("银行一天8h中接待的客户总人数为：", n)
print("每个客户的平均等待时间：")
print(t)
endTime = datetime.now()
run_time = endTime - startTime
print("整个程序运行的时间为：", run_time)

• 有约束的非线性规划问题

  • 数学规划问题分类
    

    

    

    

    

  • 仿真

    import numpy as np
n = 100000 # 模拟次数
x_1s = np.random.uniform(20,30,(n,1)) # 生成在[20,30]之间均匀分布的随机数组成的n行1列的向量构成x1
x_2s = x_1s - 10
x_3s = np.random.uniform(-10,16,(n,1)) # 生成在[-10,16]之间均匀分布的随机数组成的n行1列的向量构成x3
results = [] # 记录所有可行解的结果
for i in range(0, n):
    if ((-x_1s[i] + 2*x_2s[i] + 2*x_3s[i]) >= 0 ) and ((x_1s[i] + 2*x_2s[i] + 2*x_3s[i]) <= 72):
        results.append(x_1s[i]*x_2s[i]*x_3s[i])
f_max = max(np.array(results))[0] # 最大值
j = results.index(f_max) # 最大值索引
x_1_max = x_1s[j][0] # f(x)取最大值时，x1的值
x_2_max = x_2s[j][0] # f(x)取最大值时，x2的值
x_3_max = x_3s[j][0] # f(x)取最大值时，x3的值
print("蒙特卡洛模拟出的最大值为：{: .4f}".format(f_max))
print("蒙特卡洛模拟出最大值时x1的取值为：{: .4f}".format(x_1_max))
print("蒙特卡洛模拟出最大值时x2的取值为：{: .4f}".format(x_2_max))
print("蒙特卡洛模拟出最大值时x3的取值为：{: .4f}".format(x_3_max))

• 书店买书问题（0-1规范）
  

  

• 仿真

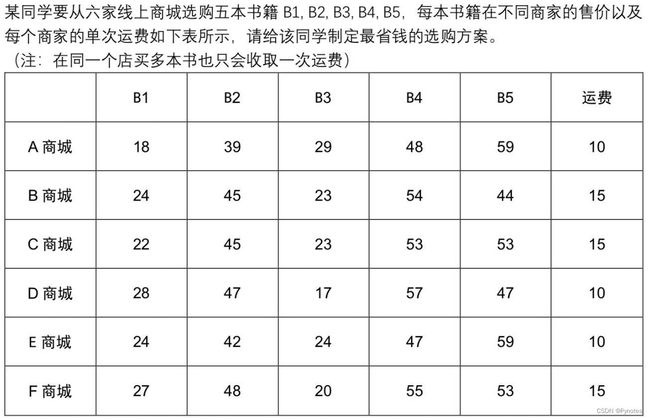
import numpy as np
n = 10000 # 模拟总次数
cost_solves = [] 
for l in range(0,n):
    i = list(range(1,7))
    j = list(range(1,6))
    M = np.array([[18,39,29,48,59],
                [24,45,23,54,44],
                [22,45,23,53,53],
                [28,47,17,57,47],
                [24,42,24,47,59],
                [27,48,20,55,53]])
    q = [10,15,15,10,10,15]
    cost = [] 
    y_fs = [] # 运费索引
    new_yfs = [] # 随机一次的运费列表
    while j:
        np.random.choice(i) # 随机选择在哪个店买书
        m = i.index(np.random.choice(i))  # 店索引
        y_fs.append(m)
        np.random.choice(j) # 随机选择买一本书
        n = j.index(np.random.choice(j)) # 书索引
        b_m = M[m][n] # 该本书的费用
        cost.append(b_m)
        j.pop(n) # 缩小样本空间
    for k in np.bincount(y_fs):
        if k != 0 :
            new_yfs.append(q[k])
    all_cost = sum(cost) + sum(new_yfs) # 一次随机的总费用 = 一次随机买书的费用总和 + 一次随机邮费总和
    cost_solves.append(all_cost) # 最小花销的索引
min_cost = min(cost_solves) # 最小花费
min_cost_index = cost_solves.index(min_cost) # 最小花费索引
print("用蒙特卡洛方法求解的最小花费为：", min_cost)
print("最小花费的位置为：", min_cost_index)

【结语】：

	至此，蒙特卡洛的的简单应用已经分享完毕，如果代码详解有什么不懂的，欢迎留言交流。