NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

Abstract.

We present a method that achieves state-of-the-art results for synthesizing novel views of complex scenes by optimizing an underlying continuous volumetric scene function using a sparse set of input views. Our algorithm represents a scene using a fully-connected (nonconvolutional) deep network, whose input is a single continuous 5D coordinate (spatial location (x, y, z) and viewing direction (θ, φ)) and whose output is the volume density and view-dependent emitted radiance at that spatial location. We synthesize views by querying 5D coordinates along camera rays and use classic volume rendering techniques to project the output colors and densities into an image. Because volume rendering is naturally differentiable, the only input required to optimize our representation is a set of images with known camera poses. We describe how to effectively optimize neural radiance fields to render photorealistic novel views of scenes with complicated geometry and appearance, and demonstrate results that outperform prior work on neural rendering and view synthesis. View synthesis results are best viewed as videos, so we urge readers to view our supplementary video for convincing comparisons.
我们提出了一种方法，通过使用稀疏的输入视图集优化底层连续的体积场景函数，实现了综合复杂场景的新颖视图的最先进的结果。我们的算法使用全连通(非卷积)深度网络表示场景，其输入是单个连续的5D坐标(空间位置(x, y, z)和观测方向(θ， φ))，其输出是该空间位置的体积密度和视相关的辐射亮度。我们通过沿着相机光线查询5D坐标来合成视图，并使用经典的体绘制技术将输出的颜色和密度投影到图像中。因为体绘制是自然可微的，优化我们的表示所需的唯一输入是一组已知相机姿态的图像。我们描述了如何有效地优化神经辐射场，以渲染具有复杂几何形状和外观的场景的逼真的新视图，并演示了优于神经渲染和视图合成之前的工作的结果。视图综合结果最好以视频的形式观看，因此我们敦促读者观看我们的补充视频，以便进行令人信服的比较。

Keywords: scene representation, view synthesis, image-based rendering, volume rendering, 3D deep learning

1 Introduction

In this work, we address the long-standing problem of view synthesis in a new way by directly optimizing parameters of a continuous 5D scene representation to minimize the error of rendering a set of captured images.
在这项工作中，我们通过直接优化连续5D场景表示的参数来解决长期存在的视图合成问题，以最大限度地减少绘制一组捕获图像的误差。

We represent a static scene as a continuous 5D function that outputs the radiance emitted in each direction (θ, φ) at each point (x, y, z) in space, and a density at each point which acts like a differential opacity controlling how much radiance is accumulated by a ray passing through (x, y, z). Our method optimizes a deep fully-connected neural network without any convolutional layers (often referred to as a multilayer perceptron or MLP) to represent this function by regressing from a single 5D coordinate (x, y, z, θ, φ) to a single volume density and view-dependent RGB color. To render this neural radiance field (NeRF) from a particular viewpoint we: 1) march camera rays through the scene to generate a sampled set of 3D points, 2) use those points and their corresponding 2D viewing directions as input to the neural network to produce an output set of colors and densities, and 3) use classical volume rendering techniques to accumulate those colors and densities into a 2D image. Because this process is naturally differentiable, we can use gradient descent to optimize this model by minimizing the error between each observed image and the corresponding views rendered from our representation. Minimizing this error across multiple views encourages the network to predict a coherent model of the scene by assigning high volume densities and accurate colors to the locations that contain the true underlying scene content. Figure 2 visualizes this overall pipeline.
我们代表一个静态场景连续5 d函数,输出每个方向发出的光辉(θ,φ)在每一个点在空间(x, y, z),和一个密度每一点它就像一个微分透明度控制积累了多少光辉的射线穿过(x, y, z)。我们的方法优化了一个没有任何卷积层(通常称为多层感知器或MLP)的深度全连接神经网络，通过从单个5D坐标(x,y,z，θ，φ)回归到单个体积密度和视相关的RGB颜色来表示这个函数。为了从一个特定的角度渲染这个神经辐射场(NeRF)，我们:(1) 3月相机光线通过场景来生成一组采样的3 d点,(2)使用这些点及其对应的2 d观看方向作为神经网络的输入产生一组输出的颜色和密度,以及(3)使用经典的体绘制技术积累这些颜色和密度为2 d图像。因为这个过程是自然可微的，我们可以使用梯度下降来优化这个模型，通过最小化每个观察到的图像和从我们的表示中呈现的相应视图之间的误差。在多个视图中最小化这个误差，鼓励网络通过分配高体积密度和准确的颜色到包含真实底层场景内容的位置来预测场景的连贯模型。图2显示了整个管道。

We find that the basic implementation of optimizing a neural radiance field representation for a complex scene does not converge to a sufficiently highresolution representation and is inefficient in the required number of samples per camera ray. We address these issues by transforming input 5D coordinates with a positional encoding that enables the MLP to represent higher frequency functions, and we propose a hierarchical sampling procedure to reduce the number of queries required to adequately sample this high-frequency scene representation.
我们发现，优化复杂场景的神经辐射场表示的基本实现不能收敛到足够高的分辨率表示，而且在每个相机射线所需的样本数量方面效率低下。我们通过使用位置编码转换输入5D坐标来解决这些问题，使MLP能够表示更高频率的函数，我们还提出了一种分层采样程序，以减少对这种高频场景表示进行充分采样所需的查询数量。

Our approach inherits the benefits of volumetric representations: both can represent complex real-world geometry and appearance and are well suited for gradient-based optimization using projected images. Crucially, our method overcomes the prohibitive storage costs of discretized voxel grids when modeling complex scenes at high-resolutions. In summary, our technical contributions are:
我们的方法继承了体积表示的优点:两者都可以表示复杂的现实世界的几何和外观，并且非常适合使用投影图像进行基于梯度的优化。至关重要的是，我们的方法克服了离散体素网格在高分辨率建模复杂场景时令人望而却步的存储成本。总之，我们的技术贡献是:

– An approach for representing continuous scenes with complex geometry and materials as 5D neural radiance fields, parameterized as basic MLP networks.
一种将具有复杂几何和材料的连续场景表示为5D神经辐射场的方法，参数化为基本MLP网络。

– A differentiable rendering procedure based on classical volume rendering techniques, which we use to optimize these representations from standard RGB images. This includes a hierarchical sampling strategy to allocate the MLP’s capacity towards space with visible scene content.
一个基于经典体绘制技术的可微分渲染过程，我们使用它来优化这些来自标准RGB图像的表示。这包括一个分层采样策略，以分配MLP的容量与可见的场景内容的空间。

– A positional encoding to map each input 5D coordinate into a higher dimensional space, which enables us to successfully optimize neural radiance fields to represent high-frequency scene content.
位置编码，将每个输入5D坐标映射到更高维度空间，使我们能够成功地优化神经辐射场，以表示高频场景内容。

We demonstrate that our resulting neural radiance field method quantitatively and qualitatively outperforms state-of-the-art view synthesis methods, including works that fit neural 3D representations to scenes as well as works that train deep convolutional networks to predict sampled volumetric representations. As far as we know, this paper presents the first continuous neural scene representation that is able to render high-resolution photorealistic novel views of real objects and scenes from RGB images captured in natural settings.
我们证明，我们产生的神经辐射场方法在定量和定性上优于最先进的视图合成方法，包括适合场景的神经三维表示，以及训练深度卷积网络预测采样体积表示的工作。据我们所知，本文提出了第一个连续的神经场景表示，它能够从自然环境中捕获的RGB图像中呈现真实物体和场景的高分辨率真实感新视图。

2 Related Work

A promising recent direction in computer vision is encoding objects and scenes in the weights of an MLP that directly maps from a 3D spatial location to an implicit representation of the shape, such as the signed distance [6] at that location. However, these methods have so far been unable to reproduce realistic scenes with complex geometry with the same fidelity as techniques that represent scenes using discrete representations such as triangle meshes or voxel grids. In this section, we review these two lines of work and contrast them with our approach, which enhances the capabilities of neural scene representations to produce state-of-the-art results for rendering complex realistic scenes.
最近计算机视觉的一个有前途的方向是用MLP的权值编码对象和场景，它直接从3D空间位置映射到形状的隐式表示，例如该位置的符号距离[6]。然而，到目前为止，这些方法还不能再现具有复杂几何形状的真实场景，与使用离散表示(如三角形网格或体素网格)的技术具有相同的保真度。在本节中，我们将回顾这两种工作方式，并将它们与我们的方法进行对比，我们的方法增强了神经场景表示的能力，从而为渲染复杂的现实场景产生最先进的结果。

A similar approach of using MLPs to map from low-dimensional coordinates to colors has also been used for representing other graphics functions such as images [44], textured materials [12,31,36,37], and indirect illumination values [38].
使用MLPs从低维坐标映射到颜色的类似方法也被用于表示其他图形功能，如图像[44]、纹理材料[12,31,36,37]和间接照明值[38]。

Neural 3D shape representations. Recent work has investigated the implicit representation of continuous 3D shapes as level sets by optimizing deep networks that map xyz coordinates to signed distance functions [15,32] or occupancy fields [11,27]. However, these models are limited by their requirement of access to ground truth 3D geometry, typically obtained from synthetic 3D shape datasets such as ShapeNet [3]. Subsequent work has relaxed this requirement of ground truth 3D shapes by formulating differentiable rendering functions that allow neural implicit shape representations to be optimized using only 2D images. Niemeyer et al. [29] represent surfaces as 3D occupancy fields and use a numerical method to find the surface intersection for each ray, then calculate an exact derivative using implicit differentiation. Each ray intersection location is provided as the input to a neural 3D texture field that predicts a diffuse color for that point. Sitzmann et al. [42] use a less direct neural 3D representation that simply outputs a feature vector and RGB color at each continuous 3D coordinate, and propose a differentiable rendering function consisting of a recurrent neural network that marches along each ray to decide where the surface is located.
神经三维形状表示。最近的工作通过优化将xyz坐标映射到符号距离函数[15,32]或占用场[11,27]的深度网络，研究了连续三维形状作为水平集的隐式表示。然而，这些模型受到真实三维几何数据访问要求的限制，通常从合成的三维形状数据集(如ShapeNet[3])获得。后续工作通过制定可微的渲染函数，允许仅使用2D图像对神经隐式形状表示进行优化，从而放宽了对真实3D形状的要求。Niemeyer等人[29]将曲面表示为三维占用场，并使用数值方法找到每条射线的曲面交点，然后使用隐式微分计算精确导数。每个光线相交的位置都作为一个神经三维纹理场的输入，预测该点的漫射颜色。Sitzmann等。[42]使用较少直接神经三维表示,只是输出一个特征向量和RGB颜色在每个连续的三维坐标,并提出一个可微的渲染函数递归神经网络组成的游行沿着射线决定表面所在地。

Though these techniques can potentially represent complicated and highresolution geometry, they have so far been limited to simple shapes with low geometric complexity, resulting in oversmoothed renderings. We show that an alternate strategy of optimizing networks to encode 5D radiance fields (3D volumes with 2D view-dependent appearance) can represent higher-resolution geometry and appearance to render photorealistic novel views of complex scenes.
虽然这些技术可以潜在地表示复杂和高分辨率的几何图形，但迄今为止，它们仅限于几何复杂性低的简单形状，导致渲染过度平滑。我们展示了一种优化网络编码5D亮度场(带有2D视图相关外观的3D体积)的替代策略，可以代表更高分辨率的几何形状和外观，以渲染复杂场景的逼真新视图。

View synthesis and image-based rendering. Given a dense sampling of views, photorealistic novel views can be reconstructed by simple light field sample interpolation techniques [21,5,7]. For novel view synthesis with sparser view sampling, the computer vision and graphics communities have made significant progress by predicting traditional geometry and appearance representations from observed images. One popular class of approaches uses mesh-based representations of scenes with either diffuse [48] or view-dependent [2,8,49] appearance. Differentiable rasterizers [4,10,23,25] or pathtracers [22,30] can directly optimize mesh representations to reproduce a set of input images using gradient descent. However, gradient-based mesh optimization based on image reprojection is often difficult, likely because of local minima or poor conditioning of the loss landscape. Furthermore, this strategy requires a template mesh with fixed topology to be provided as an initialization before optimization [22], which is typically unavailable for unconstrained real-world scenes.
视图合成和基于图像的渲染。在视图密集采样的情况下，可以通过简单的光场样本插值技术重建逼真的新视图[21,5,7]。对于具有稀疏视图采样的新型视图合成，计算机视觉和图形界已经通过从观测图像预测传统的几何和外观表征取得了重大进展。一种流行的方法是使用基于网格的场景表示，具有扩散的[48]或视相关的[2,8,49]外观。可微光栅化[4,10,23,25]或pathtracers[22,30]可以直接优化网格表示，利用梯度下降法再现一组输入图像。然而，基于图像重投影的基于梯度的网格优化通常是困难的，可能是由于局部极小值或对损失景观的不良调节。此外，该策略需要在优化[22]之前提供一个具有固定拓扑结构的模板网格作为初始化，这在没有约束的现实场景中通常是不可用的。

Another class of methods use volumetric representations to address the task of high-quality photorealistic view synthesis from a set of input RGB images. Volumetric approaches are able to realistically represent complex shapes and materials, are well-suited for gradient-based optimization, and tend to produce less visually distracting artifacts than mesh-based methods. Early volumetric approaches used observed images to directly color voxel grids [19,40,45]. More recently, several methods [9,13,17,28,33,43,46,52] have used large datasets of multiple scenes to train deep networks that predict a sampled volumetric representation from a set of input images, and then use either alpha-compositing [34] or learned compositing along rays to render novel views at test time. Other works have optimized a combination of convolutional networks (CNNs) and sampled voxel grids for each specific scene, such that the CNN can compensate for discretization artifacts from low resolution voxel grids [41] or allow the predicted voxel grids to vary based on input time or animation controls [24]. While these volumetric techniques have achieved impressive results for novel view synthesis, their ability to scale to higher resolution imagery is fundamentally limited by poor time and space complexity due to their discrete sampling — rendering higher resolution images requires a finer sampling of 3D space. We circumvent this problem by instead encoding a continuous volume within the parameters of a deep fully-connected neural network, which not only produces significantly higher quality renderings than prior volumetric approaches, but also requires just a fraction of the storage cost of those sampled volumetric representations.
另一类方法使用体积表示来解决从一组输入的RGB图像合成高质量逼真视图的任务。体积方法能够真实地表现复杂的形状和材料，非常适合基于梯度的优化，并且往往比基于网格的方法产生更少的视觉干扰。早期的体积法使用观察到的图像直接为体素网格着色[19,40,45]。最近,几个方法[9,13,17,28,33,43,46,52] 使用大型数据集的多个场景训练深度网络预测采样体积表示的输入图像,然后使用alpha-compositing[34]或学会合成沿着光线渲染小说的看法在测试时间。其他工作已经优化了卷积网络(CNN)和采样体素网格的组合针对每个特定场景，这样CNN可以补偿来自低分辨率体素网格的离散化工件[41]或允许预测体素网格根据输入时间或动画控制[24]而变化。虽然这些体积技术已经在新的视图合成方面取得了令人印象深刻的结果，但由于其离散采样，它们缩放到更高分辨率图像的能力从根本上受到时间和空间复杂性的限制——渲染更高分辨率的图像需要对3D空间进行更精细的采样。我们通过在深度全连接神经网络的参数内编码连续的体积来绕过这个问题，这不仅比之前的体积方法产生更高质量的渲染，而且只需要那些采样体积表示的一小部分存储成本。

3 Neural Radiance Field Scene Representation

We represent a continuous scene as a 5D vector-valued function whose input is a 3D location x = (x, y, z) and 2D viewing direction (θ, φ), and whose output is an emitted color c = (r, g, b) and volume density σ. In practice, we express direction as a 3D Cartesian unit vector d. We approximate this continuous 5D scene representation with an MLP network FΘ : (x, d) → (c, σ) and optimize its weights Θ to map from each input 5D coordinate to its corresponding volume density and directional emitted color.
我们将一个连续场景表示为一个5D向量值函数，它的输入是一个3D位置x = (x, y, z)和2D观测方向(θ， φ)，它的输出是一个发出的颜色c = (r, g, b)和体积密度σ。在实践中,我们表达方向三维笛卡尔单位矢量d。我们近似连续5d场景代表的MLP网络FΘ:(x, d)→(c,σ)和优化其权重Θ从每个输入5d坐标映射到相应的体积密度和定向发射的颜色。

We encourage the representation to be multiview consistent by restricting the network to predict the volume density σ as a function of only the location x, while allowing the RGB color c to be predicted as a function of both location and viewing direction. To accomplish this, the MLP FΘ first processes the input 3D coordinate x with 8 fully-connected layers (using ReLU activations and 256 channels per layer), and outputs σ and a 256-dimensional feature vector. This feature vector is then concatenated with the camera ray’s viewing direction and passed to one additional fully-connected layer (using a ReLU activation and 128 channels) that output the view-dependent RGB color.
我们通过限制网络预测体积密度σ仅作为位置x的函数，而允许RGB颜色c作为位置和观测方向的函数进行预测，从而鼓励表示为多视图一致。为了实现这一点，MLP FΘ首先处理具有8个全连接层的输入3D坐标x(使用ReLU激活，每层256个通道)，并输出σ和256维特征向量。这个特征向量然后与相机射线的观看方向连接，并传递给一个额外的全连接层(使用ReLU激活和128通道)，输出视相关的RGB颜色。

See Fig. 3 for an example of how our method uses the input viewing direction to represent non-Lambertian effects. As shown in Fig. 4, a model trained without view dependence (only x as input) has difficulty representing specularities.
图3是我们的方法如何使用输入视图方向来表示非朗伯效应的示例。如图4所示，一个不依赖于视图(只有x作为输入)的模型很难表示投机性。

4 Volume Rendering with Radiance Fields

Our 5D neural radiance field represents a scene as the volume density and directional emitted radiance at any point in space. We render the color of any ray passing through the scene using principles from classical volume rendering [16]. The volume density σ(x) can be interpreted as the differential probability of a ray terminating at an infinitesimal particle at location x. The expected color C® of camera ray r(t)=o+td with near and far bounds tn and tf is:
我们的5D神经辐射场表示场景为空间中任意点的体积密度和定向发射的辐射。我们使用经典体积渲染[16]的原理来渲染任何穿过场景的光线的颜色。体积密度σ(x)可理解为射线在位置x处终止于无穷小粒子的微分概率。摄像机射线r(t)=o+td，近界和远界tn和tf的期望颜色C®为:

The function T(t) denotes the accumulated transmittance along the ray from tn to t, i.e., the probability that the ray travels from tn to t without hitting any other particle. Rendering a view from our continuous neural radiance field requires estimating this integral C® for a camera ray traced through each pixel of the desired virtual camera.
函数T(t)表示从tn到T射线的累计透射率，即射线从tn到T不撞击任何其他粒子的概率。从我们的连续神经辐射场渲染一个视图需要估计这个积分C®的相机射线跟踪通过所需的虚拟相机的每个像素。

We numerically estimate this continuous integral using quadrature. Deterministic quadrature, which is typically used for rendering discretized voxel grids, would effectively limit our representation’s resolution because the MLP would only be queried at a fixed discrete set of locations. Instead, we use a stratified sampling approach where we partition [tn, tf] into N evenly-spaced bins and then draw one sample uniformly at random from within each bin:
我们用求积法对这个连续积分进行了数值估计。确定性求积法通常用于绘制离散体素网格，它将有效地限制我们表示的分辨率，因为MLP只会在固定的离散位置集上查询。相反，我们使用分层抽样方法，将[tn, tf]划分到N个等间距的箱子中，然后从每个箱子中均匀随机抽取一个样本:

Although we use a discrete set of samples to estimate the integral, stratified sampling enables us to represent a continuous scene representation because it results in the MLP being evaluated at continuous positions over the course of optimization. We use these samples to estimate C® with the quadrature rule discussed in the volume rendering review by Max [26]:
虽然我们使用离散的样本集来估计整体，但分层抽样使我们能够表示连续的场景表示，因为它导致在优化过程中在连续的位置评估MLP。我们使用这些样本来估计C®与Max[26]的体积渲染评论中讨论的正交规则:

where δi = t(i+1) − ti is the distance between adjacent samples. This function for calculating ˆC® from the set of (ci, σi) values is trivially differentiable and reduces to traditional alpha compositing with alpha values αi = 1 − exp(−σiδi).
式中δi = t(i+1)−ti为相邻样本间的距离。从(ci， σi)值的集合中计算ˆC( r) 的函数是平凡可微的，可以简化为传统的α合成αi = 1−exp(−σiδi)。

5 Optimizing a Neural Radiance Field

In the previous section we have described the core components necessary for modeling a scene as a neural radiance field and rendering novel views from this representation. However, we observe that these components are not sufficient for achieving state-of-the-art quality, as demonstrated in Section 6.4). We introduce two improvements to enable representing high-resolution complex scenes. The first is a positional encoding of the input coordinates that assists the MLP in representing high-frequency functions, and the second is a hierarchical sampling procedure that allows us to efficiently sample this high-frequency representation.
在上一节中，我们已经描述了将场景建模为神经辐射场和从这个表示呈现新视图所需的核心组件。然而，我们注意到，如章节6.4所示，这些组件不足以达到最先进的质量。我们引入了两个改进来实现高分辨率复杂场景的表示。第一个是输入坐标的位置编码，帮助MLP表示高频函数，第二个是分层采样程序，允许我们有效地对高频表示进行采样。

5.1 Positional encoding

Despite the fact that neural networks are universal function approximators [14], we found that having the network FΘ directly operate on xyzθφ input coordinates results in renderings that perform poorly at representing high-frequency variation in color and geometry. This is consistent with recent work by Rahaman et al. [35], which shows that deep networks are biased towards learning lower frequency functions. They additionally show that mapping the inputs to a higher dimensional space using high frequency functions before passing them to the network enables better fitting of data that contains high frequency variation.
尽管神经网络是通用函数近似器[14]，但我们发现，让网络FΘ直接作用于xyzθφ输入坐标，导致渲染图在表示颜色和几何形状的高频变化方面表现不佳。这与Rahaman等人[35]最近的研究一致，该研究表明，深度网络偏向于学习低频函数。他们还表明，在将输入数据传递到网络之前，使用高频函数将输入映射到更高维度空间，能够更好地拟合包含高频变化的数据。

We leverage these findings in the context of neural scene representations, and show that reformulating FΘ as a composition of two functions FΘ=FΘ’◦γ, one learned and one not, significantly improves performance (see Fig. 4 and Table 2). Here γ is a mapping from R into a higher dimensional space R2L, and F 0Θ is still simply a regular MLP. Formally, the encoding function we use is:
我们利用这些发现在神经场景表示,和显示调整FΘ组成的两个函数FΘ= FΘ◦γ,一个学习,一个不是,极大地提高了性能(见图4和表2)。这里γ从R是一个映射到一个高维空间R2L和F 0Θ仍只是一个常规的中长期规划。形式上，我们使用的编码函数是:

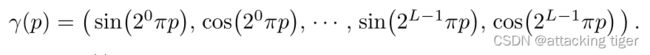
This function γ(·) is applied separately to each of the three coordinate values in x (which are normalized to lie in [−1, 1]) and to the three components of the Cartesian viewing direction unit vector d (which by construction lie in [−1, 1]). In our experiments, we set L = 10 for γ(x) and L = 4 for γ(d).
函数γ(·)分别应用于x中的三个坐标值(归一化为位于[−1,1])和笛卡尔视向单位向量d的三个分量(构造为[−1,1])。在我们的实验中，我们设置L = 10的γ(x)和L = 4的γ(d)。

A similar mapping is used in the popular Transformer architecture [47], where it is referred to as a positional encoding. However, Transformers use it for a different goal of providing the discrete positions of tokens in a sequence as input to an architecture that does not contain any notion of order. In contrast, we use these functions to map continuous input coordinates into a higher dimensional space to enable our MLP to more easily approximate a higher frequency function. Concurrent work on a related problem of modeling 3D protein structure from projections [51] also utilizes a similar input coordinate mapping.
在流行的Transformer体系结构[47]中也使用了类似的映射，在这里它被称为位置编码。然而，transformer使用它的另一个目的是提供序列中标记的离散位置，作为不包含任何顺序概念的体系结构的输入。相反，我们使用这些函数将连续的输入坐标映射到更高的维度空间，使我们的MLP更容易接近更高频率的函数。通过投影[51]对三维蛋白质结构进行建模的相关问题的并行工作也使用了类似的输入坐标映射。

5.2 Hierarchical volume sampling

Our rendering strategy of densely evaluating the neural radiance field network at N query points along each camera ray is inefficient: free space and occluded regions that do not contribute to the rendered image are still sampled repeatedly. We draw inspiration from early work in volume rendering [20] and propose a hierarchical representation that increases rendering efficiency by allocating samples proportionally to their expected effect on the final rendering.
我们的渲染策略是沿着每个相机射线密集评估N个查询点的神经辐射场网络是低效的:对渲染图像没有贡献的自由空间和遮挡区域仍然被重复采样。我们从早期的体积渲染[20]的工作中获得灵感，并提出了一种分层表示，通过按最终渲染的预期效果比例分配样本来提高渲染效率。

Instead of just using a single network to represent the scene, we simultaneously optimize two networks: one “coarse” and one “fine”. We first sample a set of Nc locations using stratified sampling, and evaluate the “coarse” network at these locations as described in Eqns. 2 and 3. Given the output of this “coarse” network, we then produce a more informed sampling of points along each ray where samples are biased towards the relevant parts of the volume. To do this, we first rewrite the alpha composited color from the coarse network ˆCc® in Eqn. 3 as a weighted sum of all sampled colors ci along the ray:
我们不是只用一个网络来表示场景，而是同时优化两个网络:一个“粗”和一个“精”。我们首先使用分层抽样的方法对一组Nc位置进行抽样，并按照Eqns. 2和3所述的方法对这些位置的“粗”网络进行评估。考虑到这个“粗糙”网络的输出，然后我们沿着每条射线产生一个更有信息的点采样，这些点的样本都偏向于体积的相关部分。为了做到这一点，我们首先重写Eqn. 3中粗糙网络ˆCc®的alpha合成颜色，作为沿着射线的所有采样颜色ci的加权和:

Normalizing these weights as ˆwi = wi/PNcj=1 wj produces a piecewise-constant PDF along the ray. We sample a second set of Nf locations from this distribution using inverse transform sampling, evaluate our “fine” network at the union of the first and second set of samples, and compute the final rendered color of the ray ˆCf ® using Eqn. 3 but using all Nc +Nf samples. This procedure allocates more samples to regions we expect to contain visible content. This addresses a similar goal as importance sampling, but we use the sampled values as a nonuniform discretization of the whole integration domain rather than treating each sample as an independent probabilistic estimate of the entire integral.
将这些权重归一化为ˆwi = wi/PNcj= 1wj，将产生一个沿射线分段恒定的PDF。我们使用反变换采样从这个分布中采样第二组Nf位置，评估第一组和第二组样本的并集，并使用Eqn. 3计算射线ˆCf ®的最终渲染颜色，但使用所有Nc +Nf样本。这个过程分配更多的样本到我们希望包含可见内容的区域。这与重要性抽样的目标相似，但我们使用采样值作为整个积分域的非均匀离散化，而不是将每个样本作为整个积分的独立概率估计。

5.3 Implementation details

We optimize a separate neural continuous volume representation network for each scene. This requires only a dataset of captured RGB images of the scene, the corresponding camera poses and intrinsic parameters, and scene bounds (we use ground truth camera poses, intrinsics, and bounds for synthetic data, and use the COLMAP structure-from-motion package [39] to estimate these parameters for real data). At each optimization iteration, we randomly sample a batch of camera rays from the set of all pixels in the dataset, and then follow the hierarchical sampling described in Sec. 5.2 to query Nc samples from the coarse network and Nc + Nf samples from the fine network. We then use the volume rendering procedure described in Sec. 4 to render the color of each ray from both sets of samples. Our loss is simply the total squared error between the rendered and true pixel colors for both the coarse and fine renderings:
我们为每个场景优化了单独的连续神经体积表示网络。这只需要一个数据集的RGB图像捕获的场景,相应的相机姿态和内在参数,现场范围(我们使用地面实况相机姿势、intrinsic和边界合成数据,并使用COLMAP structure-from-motion包[39]估计这些参数真实数据)。在每次优化迭代中，我们从数据集中所有像素的集合中随机抽取一批相机射线，然后按照5.2节所述的分层抽样，从粗网络中查询Nc样本，从精细网络中查询Nc + Nf样本。然后我们使用第4节中描述的体积渲染程序来渲染来自两组样本的每条射线的颜色。我们的损失只是粗略和精细渲染的渲染和真实像素颜色之间的总平方误差:

where R is the set of rays in each batch, and C®, ˆCc®, and ˆCf ® are the ground truth, coarse volume predicted, and fine volume predicted RGB colors for ray r respectively. Note that even though the final rendering comes from ˆCf ®, we also minimize the loss of ˆCc® so that the weight distribution from the coarse network can be used to allocate samples in the fine network.
其中R为每批射线的集合，C®、ˆCc®、ˆCf ®分别为射线R的ground truth、粗体积预测、细体积预测RGB颜色。注意，尽管最终的渲染来自ˆCf ®，我们也最小化了ˆCc®的损失，这样粗网络的权重分布可以用于在细网络中分配样本。

In our experiments, we use a batch size of 4096 rays, each sampled at Nc = 64 coordinates in the coarse volume and Nf = 128 additional coordinates in the fine volume. We use the Adam optimizer [18] with a learning rate that begins at 5 × 10−4 and decays exponentially to 5 × 10−5 over the course of optimization (other Adam hyperparameters are left at default values of β1 = 0.9, β2 = 0.999, and ? = 10−7). The optimization for a single scene typically take around 100– 300k iterations to converge on a single NVIDIA V100 GPU (about 1–2 days).
在我们的实验中，我们使用4096条射线，每条射线在粗体积中Nc = 64坐标和在细体积中Nf = 128额外坐标采样。我们使用Adam优化器[18]，其学习速率从5 × 10−4开始，在优化过程中指数衰减到5 × 10−5(其他Adam超参数保留默认值β1 = 0.9， β2 = 0.999，和?= 10−7)。对单个场景的优化通常需要大约100 - 300k次迭代才能汇聚到单个NVIDIA V100 GPU上(大约1-2天)。