Robust Data Partitioning for Ad-hoc Query Processing论文阅读
目录
- Robust Data Partitioning for Ad-hoc Query Processing
- 超分区树的selection
- 超分区树的join
- join分区分组方法
-
- 算法1:Index Nested Loop Join
- 算法1b:Index Nested Loops, Split
- 算法2:Minimizing Replication of the Larger Table
- 算法3:Bottom-up Grouping
Robust Data Partitioning for Ad-hoc Query Processing
2015,MIT
分区分为数据范围分区和哈希分区,但都不能解决查询工作负载是临时的和不可预测的情况。
数据库分区涉及将数据库中的数据划分为单独的物理部分。这样做通常有三个主要原因:分发数据、容忍故障或提高性能(to distribute data, to tolerate failures, or to improve performance)。例如,如果数据集太大,无法存储在单个机器上,则可以将其划分为多个部分,以分布在机器集群中。每个分区可以存储在一台机器上,也可以存储在多台机器上以实现容错。分区也不仅仅是在机器之间划分数据。可以在每台机器内进一步划分数据以提高性能。
如果数据集基于查询所涉及的同一属性进行分区,则该查询的性能会显著提高,因为系统可以使用分区信息跳过与查询不匹配的分区。跳过的不匹配分区作为分区方法的评价标准。
在最传统的方法中,数据库是基于单个属性进行分区的。这个分区属性通常是最耗时或最频繁的查询所使用的属性。还提出了许多更复杂的数据分区技术,但它们都基于预期运行或过去运行的查询类型来构造分区。
超出预期工作负载的查询仍将执行不良。这些类型的技术不适用于我们正在考虑的特殊查询,因为在这种情况下,查询工作负载是先验未知的。我们希望有一种数据分区技术,它可以为所有类型的可能查询提供性能增益,而不仅仅是一些受限集内的查询。
我们提出的解决方案是超分区系统。它旨在以两种方式支持自组织查询处理:第一,创建一个初始的健壮分区,为数据集中每个属性的查询提供平衡的性能改进;第二,通过逐步调整分区以响应实际工作负载,在出现特定工作负载时提供更好的性能。
最后,数据库破解(database cracking)是一种自适应划分数据集并建立索引的技术,数据集不是预先一次分区的。相反,在处理查询时,每个查询中的属性用于决定如何将数据分割成更细粒度的分区。因此,前几个查询并没有得到那么多的好处。此外,属性只能独立破解,并且必须提前选择破解属性。
默认情况下,HDFS仅根据大小将数据集划分为大小均匀的块,而不考虑块的内容。HDFS之上的各种数据处理工具,例如Pig、Hive和Impala,增加了对基于属性的分区的支持。这些工具只是创建传统的单属性分区,但仍然为开发人员提供了一些优化工作负载数据布局的能力。
研究人员还构建了HDFS的扩展,能够在给定查询工作负载信息的情况下进行更高级的分区。Hadoop++可以在块内对数据进行共分区,以提高连接效率,而CoHadoop可以对相关分区进行共定位。
传统的kd-tree按照属性的顺序依次划分节点,当划分层数小于属性个数时则省略末尾属性。
超分区树的每一枝都可能按照不同的属性划分,并且保证每个属性至少在一个分支中。因此,超分区树可以看作kd-tree的异构。
超分区树的selection
对于查询语句,选择查询检索满足数据集属性上谓词组合的记录。例如,可能的谓词可能是‘r.id = 100’, ‘r.age > 30’, 或者‘r.gender = F’。
• 如果节点与谓词的属性不同,则该节点无助于缩小搜索范围,必须搜索其两个子树。
• 如果节点的鉴别器与谓词匹配,则根据树的搜索属性,知道左子树中的所有记录小于或等于节点的值,右子树中记录大于其值。根据谓词中运算符和常量的值,搜索左子树、右子树或两个子树。
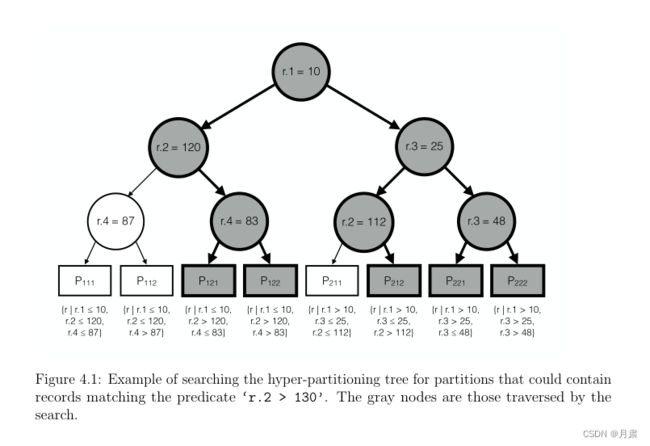
超分区树的join
如果已经存在连接谓词的co-partitioning,则计算equijoin的速度会快得多。但是,一对表只能在一个属性上进行co-partitioning,因此只有该属性上的Equijoin属性受益。要对其他属性上的表执行Equijoin,通常必须重新分区数据。
如图,将两个表分区,在范围相近的分区内进行连接。
但是数据分区往往并不如上图般理想化,如下图
不妨假设有表r, s,连接的是r.a和s.b,即 r ⋈ r . a = s . b s r\Join_{r.a=s.b} s r⋈r.a=s.bs,如上图a, b,分区join之后发现存在两个重复读取的块(图c中标红)。
设两个表R,S,分区 R i , S i R_{i}, S_{i} Ri,Si
R = ⋃ R i S = ⋃ S i R=\bigcup R_{i} \\ S=\bigcup S_{i} R=⋃RiS=⋃Si
引入
{ G i } = { ( G R i , G S i ) } \{G_{i}\} =\{(GR_{i}, GS_{i})\} {Gi}={(GRi,GSi)}
其中
G R i ⊆ { R i } G S i ⊆ { S i } GR_{i}\subseteq \{R_{i}\}\\ GS_{i}\subseteq \{S_{i}\} GRi⊆{Ri}GSi⊆{Si}
则
⋃ i { ( r , s ) ∈ ( G R i × G S i ) ∣ r . k e y R = s . k e y S } = { ( r , s ) ∈ ( R × S ) ∣ r . k e y R = s . k e y S } \bigcup_{i}\{(r, s)\in (GR_{i} \times GS_{i})|r.keyR=s.keyS\}=\{(r, s)\in (R\times S)|r.keyR=s.keyS\} i⋃{(r,s)∈(GRi×GSi)∣r.keyR=s.keyS}={(r,s)∈(R×S)∣r.keyR=s.keyS}
由于存在重复读取情况,因此需要寻找最佳分区join方案,在这里给出评价标准:
arg min G i ∑ G i ∈ { G i } ∣ G i ∣ \arg \min_{G_{i}} \sum_{G_{i}\in\{G_{i}\}}\vert G_{i}\vert argGiminGi∈{Gi}∑∣Gi∣
该方法应该比重新构造分区更快,同时我们认为如果分区读取的总量不超过表大小总和的两倍,则使用粗略的co-partitioning将是有利的。
join分区分组方法
算法1:Index Nested Loop Join
直接按照当前最小的分区进行连接,但是缺点是重复读取分区过多。
算法1b:Index Nested Loops, Split
改进于算法1,增大每组join的范围,减少join的分组个数,这样就会减少重复读取的分区。但是由于join分组减少,计算的并行性下降。在这里提出并行性计算的横向分组,即将join分组中对应分区集合较大的那个表的分区集合再进行拆分,分发到分布式机器上,同时复制分区集合较小的表的分区集合至各个分布式机器上,以此来提升分布式计算效率。
算法2:Minimizing Replication of the Larger Table
如果较大的表明显大于较小的表,那么应尽量避免对较大的表的复制,宁愿较小的表的复制增加。
在这里我们先对较大的分区和与之对应的较小分区集合进行join,从而减少较大分区的重复复制,进而以此递推。
但是,对于分区过大的话可能会引起一些内存方面的问题。
算法3:Bottom-up Grouping
首先根据自身粒度划分join key domain,对较大表中的分区进行单独分组,并且每个分区对应的较小表的分区也在分组中。初始化完成后进行分组合并,直到达到预期分组数:
- 分组的较小表分区比较相似时可以合并;
- 分组的较大表分区相同时可以合并;
- 合并时,必须遵守最大哈希输入大小的约束。此外,如果我们正在优化并行性,最终组的大小应该相当平衡,这可以通过对组的最大总大小施加额外限制来实现。
- 执行最大程度地减少输入大小的合并,同时遵循约束。




