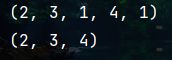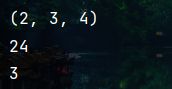论文研读番外篇(1)——pytorch、numpy的使用整理
torch、numpy和pandas的使用整理
- 一.numpy \textbf{一.numpy} 一.numpy
-
- 1.创建数组
-
- (1)创建单位矩阵 ( n u m p y . i d e n t i t y ) (numpy.identity) (numpy.identity)
- (2)创建任意shape的全零多维数组 ( n u m p y . z e r o s ) (numpy.zeros) (numpy.zeros)
- (3)创建任意shape的标准正态分布的多维数组 ( n u m p y . r a n d o m . r a n d n ) (numpy.random.randn) (numpy.random.randn)
- (4)创建任意shape的0到1的随机多维数组 ( n u m p y . r a n d o m . r a n d ) (numpy.random.rand) (numpy.random.rand)
- (5)创建任意shape的low到high的随机整型多维数组 ( n u m p y . r a n d o m . r a n d i n t ) (numpy.random.randint) (numpy.random.randint)
- (6)创建任意shape的空的多维数组 ( n u m p y . e m p t y ) (numpy.empty) (numpy.empty)
- (7)创建一个一维数组,其元素为指定间隔内均匀间隔的数字 ( n u m p y . l i n s p a c e ) (numpy.linspace) (numpy.linspace)
- 2.常用数组操作
-
- (1)按行按列拼接 ( n u m p y . v s t a c k 、 n u m p y . h s t a c k 、 n u m p y . c o l u m n s t a c k ) (numpy.vstack、numpy.hstack、numpy.column_stack) (numpy.vstack、numpy.hstack、numpy.columnstack)
- (2)数组转置 ( a r r a y . T ) (array.T) (array.T)
- (3)多维数组维度切换 ( n u m p y . t r a n s p o s e ) (numpy.transpose) (numpy.transpose)
- (4)消除数组中维数为1的维度 ( n u m p y . s q u e e z e ) (numpy.squeeze) (numpy.squeeze)
- (5)改变数组shape ( n u m p y . r e s h a p e ) (numpy.reshape) (numpy.reshape)
- (6)将相同shape的两个数组中的元素放到1个一维数组中 ( n u m p y . a p p e n d ) (numpy.append) (numpy.append)
- (7)返回满足条件的索引 ( n u m p y . w h e r e ) (numpy.where) (numpy.where)
- (8)获取数组形状、大小和维度数量 ( n u m p y . s h a p e 和 n u m p y . s i z e ) (numpy.shape和numpy.size) (numpy.shape和numpy.size)
- 3.数组计算
-
- (1)奇异值分解 ( n u m p y . l i n a l g . s v d ( 张 量 或 n u m p y 数 组 ) ) (numpy.linalg.svd(张量或numpy数组)) (numpy.linalg.svd(张量或numpy数组))
- (2)求范数 ( n u m p y . l i n a l g . n o r m ( d , o r d = 1 ) 可 任 意 s h a p e ) (numpy.linalg.norm(d, ord=1) 可任意shape) (numpy.linalg.norm(d,ord=1)可任意shape)
- (3)求内积 n u m p y . v d o t ( 数 组 或 张 量 , 数 组 或 张 量 ) numpy.vdot(数组或张量,数组或张量) numpy.vdot(数组或张量,数组或张量)
- (4)求向量中所有元素的乘积 ( n u m p y . p r o d ) (numpy.prod) (numpy.prod)
- (5)numpy简单计算 ( n u m p y . a b s 、 n u m p y . s q r t 、 n u m p y . m a x 、 n u m p y . m e a n 、 n u m p y . s t d 、 n u m p y . s u m ) (numpy.abs、numpy.sqrt、numpy.max、numpy.mean、numpy.std、numpy.sum) (numpy.abs、numpy.sqrt、numpy.max、numpy.mean、numpy.std、numpy.sum)
- (6)矩阵乘积和矩阵对应元素相乘 ( n u m p y . m a t m u l 、 n u m p y . m u l t i p l y ) (numpy.matmul、numpy.multiply) (numpy.matmul、numpy.multiply)
- (7)共轭 ( n u m p y . c o n j ) (numpy.conj) (numpy.conj)
- (8)求迹(numpy.trace)
- (9)爱因斯坦求和约定 ( n u m p y . e n i s u m ) (numpy.enisum) (numpy.enisum)
- 二.torch \textbf{二.torch} 二.torch
-
- 1.创建张量
-
- (1)生成全1张量 ( t o r c h . o n e s ) (torch.ones) (torch.ones)
- (2)生成全0张量 ( t o r c h . z e r o s ) (torch.zeros) (torch.zeros)
- (3)生成空张量 ( t o r c h . e m p t y ) (torch.empty) (torch.empty)
- (4)生成一维均匀分布张量 ( t o r c h . l i n s p a c e ) (torch.linspace) (torch.linspace)
- (5)生成数值在一定范围内的整型张量 ( t o r c h . r a n d i n t ) (torch.randint) (torch.randint)
- (6)将列表或数组强制转换为torch tensor ( t o r c h . t e n s o r ) (torch.tensor) (torch.tensor)
- (7)返回一个符合均值为0,方差为1的正态分布(标准正态分布)中填充随机数的张量 ( t o r c h . r a n d n ) (torch.randn) (torch.randn)
- 2.常用张量操作
-
- (1)张量转置和维度转换 ( t e n s o r . t ( ) 、 t e n s o r . p e r m u t e ) (tensor.t()、tensor.permute) (tensor.t()、tensor.permute)
- (2)改变shape ( t o r c h . r e s h a p e ) (torch.reshape) (torch.reshape)
- (3)张量拼接 ( t o r c h . c a t ) (torch.cat) (torch.cat)
- (4)张量拷贝 ( t e n s o r A . c o p y ( t e n s o r B ) ) (tensorA.copy_(tensorB)) (tensorA.copy(tensorB))
- (5)获取张量shape ( t e n s o r . s h a p e 、 t e n s o r . s i z e ( ) ) (tensor.shape、tensor.size()) (tensor.shape、tensor.size())
- (6)
- 3.张量计算
-
- (1)缩并 ( t o r c h . t e n s o r d o t ) (torch.tensordot) (torch.tensordot)
- (2)hadmard积实现对应元素相乘 ( ∗ ) (*) (∗)
- (3)矩阵乘积 ( @ ) (@) (@)
- (4)张量除法 ( t o r c h . f l o o r d i v i d e 、 t o r c h . t r u e d i v i d e ) (torch.floor_divide、torch.true_divide) (torch.floordivide、torch.truedivide)
- (5)爱因斯坦求和约定 ( t c . e i n s u m ) (tc.einsum) (tc.einsum)
- (6)其他的一些计算
- 4.数据类型强制转换
- 三.拓展 \textbf{三.拓展} 三.拓展:
-
- (1)tensor与numpy之间的转换
- (2)ncon.ncon
- (3)torch还可以用于深度学习(这一部分之后就可以不用看了,没有整理完,且短期可能不会再对其进行整理)
-
- 优化器
- 损失函数(目前的理解是只要开启求导,使其可以反向传播即可)
- 激活函数
- 已经封装好的层和模型(下面仅列出几个)
一.numpy \textbf{一.numpy} 一.numpy
1.创建数组
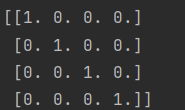
(1)创建单位矩阵 ( n u m p y . i d e n t i t y ) (numpy.identity) (numpy.identity)
import numpy as np
array = np.identity(4)
print(array)
(2)创建任意shape的全零多维数组 ( n u m p y . z e r o s ) (numpy.zeros) (numpy.zeros)
import numpy as np
# 提供列表或元组类型的shape
array = np.zeros((1, 2, 3))
print(array)
array = np.zeros([1, 2, 3])
print(array)
(3)创建任意shape的标准正态分布的多维数组 ( n u m p y . r a n d o m . r a n d n ) (numpy.random.randn) (numpy.random.randn)
# 提供shape是一个个整数,不能是list或tuple
import numpy as np
array = np.random.randn(3, 3)
print(array)
(4)创建任意shape的0到1的随机多维数组 ( n u m p y . r a n d o m . r a n d ) (numpy.random.rand) (numpy.random.rand)
import numpy as np
array = np.random.rand(3, 4)
print(array)
import numpy as np
array = np.random.random((3, 4))
print(array)
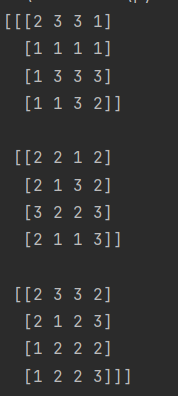
(5)创建任意shape的low到high的随机整型多维数组 ( n u m p y . r a n d o m . r a n d i n t ) (numpy.random.randint) (numpy.random.randint)
import numpy as np
array = np.random.randint(low=1, high=4, size=(3, 4, 4))
print(array)
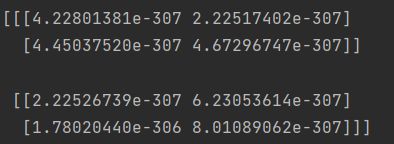
(6)创建任意shape的空的多维数组 ( n u m p y . e m p t y ) (numpy.empty) (numpy.empty)
import numpy as np
array = np.empty((2, 2, 2))
print(array)
(7)创建一个一维数组,其元素为指定间隔内均匀间隔的数字 ( n u m p y . l i n s p a c e ) (numpy.linspace) (numpy.linspace)
import numpy as np
print(np.linspace(start=1, stop=100, num=10))
print(np.linspace(start=1, stop=100, num=10).shape)
2.常用数组操作
(1)按行按列拼接 ( n u m p y . v s t a c k 、 n u m p y . h s t a c k 、 n u m p y . c o l u m n s t a c k ) (numpy.vstack、numpy.hstack、numpy.column_stack) (numpy.vstack、numpy.hstack、numpy.columnstack)
import numpy as np
array1 = np.random.randint(1, 4, (2, 4, 5))
array2 = np.random.randint(5, 6, (2, 4, 5))
# 按行拼接
new_array = np.vstack((array1, array2, array2))
print(new_array.shape)
# 按列拼接
new_array = np.hstack((array1, array2, array2))
print(new_array.shape)
vstack和hstack允许提供多维数组在第一个维度和第二个维度上的拼接,而且不限制多维数组的个数,要求就是在拼接时多维数组除了拼接维度可以不一样以外,其他维度必须保持一致。
另一个按列拼接的函数是column_stack,和hstack是差不多的,它们是有区别的,我以前在使用时有时候hstack是用不了的,但是column_stack是用不了的,具体原因记不到了,如果hstack用不了就试试column_stack吧。
import numpy as np
array1 = np.random.randint(1, 4, (2, 4, 5, 5))
array2 = np.random.randint(5, 6, (2, 4, 5, 5))
new_array = np.column_stack((array1, array2, array1, array2))
print(new_array.shape)
(2)数组转置 ( a r r a y . T ) (array.T) (array.T)
支持任意shape的numpy数组进行转置。
import numpy as np
array1 = np.random.randint(1, 10, size=(2, 3, 4))
array2 = tc.randint(1, 10, size=(2, 3, 4, 5))
print(array1.shape)
array1 = array1.T
print(array1.shape)
array1 = array1.T
print(array1.shape)
array1 = array1.T
print(array1.shape)
(3)多维数组维度切换 ( n u m p y . t r a n s p o s e ) (numpy.transpose) (numpy.transpose)
不提供axes则与T同样效果,提供axes可以对任意维度进行维度转换。
import numpy as np
import torch as tc
array1 = np.random.randint(1, 10, size=(2, 3, 4))
array2 = tc.randint(1, 10, size=(2, 3, 4, 5))
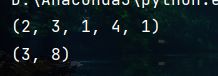
print(array1.shape)
array1 = np.transpose(array1)
print(array1.shape)
array1 = np.transpose(array1, axes=[0, 2, 1])
print(array1.shape)
(4)消除数组中维数为1的维度 ( n u m p y . s q u e e z e ) (numpy.squeeze) (numpy.squeeze)
import numpy as np
array1 = np.random.randint(1, 10, size=(2, 3, 1, 4, 1))
print(array1.shape)
print(np.squeeze(array1).shape)
(5)改变数组shape ( n u m p y . r e s h a p e ) (numpy.reshape) (numpy.reshape)
import numpy as np
array1 = np.random.randint(1, 10, size=(2, 3, 1, 4, 1))
print(array1.shape)
print(np.reshape(array1, newshape=(3, 8)).shape)
(6)将相同shape的两个数组中的元素放到1个一维数组中 ( n u m p y . a p p e n d ) (numpy.append) (numpy.append)
将后一个数组的元素加到前一个数组的元素后面。
import numpy as np
array1 = np.random.randint(1, 10, size=(3, 2, 3))
print(array1.shape)
array1 = np.append(array1, array1)
print(array1.shape)
(7)返回满足条件的索引 ( n u m p y . w h e r e ) (numpy.where) (numpy.where)
import numpy as np
array1 = np.random.randint(1, 10, size=(3, 2))
print(array1)
# 获取大于5的元素的索引并提取出来
print(np.where(array1 > 5))
print(array1[np.where(array1 > 5)])
# 将大于5的转换为1,否则为0
print(np.where(array1 > 5, 1, 0))
(8)获取数组形状、大小和维度数量 ( n u m p y . s h a p e 和 n u m p y . s i z e ) (numpy.shape和numpy.size) (numpy.shape和numpy.size)
import numpy as np
array1 = np.random.randint(1, 10, size=(2, 3, 4))
print(array1.shape)
print(array1.size)
print(np.ndim(array1))
3.数组计算
(1)奇异值分解 ( n u m p y . l i n a l g . s v d ( 张 量 或 n u m p y 数 组 ) ) (numpy.linalg.svd(张量或numpy数组)) (numpy.linalg.svd(张量或numpy数组))
import numpy as np
import torch as tc
import numpy.linalg as linalg
array1 = np.random.randint(1, 10, size=(3, 4))
array2 = np.random.randint(1, 10, size=(3, 4, 5, 6))
array3 = tc.randint(1, 10, size=(3, 4, 5))
array4 = tc.randint(1, 10, size=(3, 4, 5))
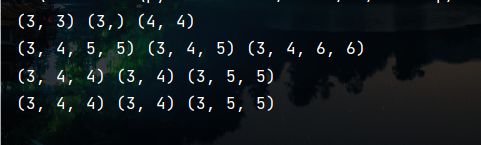
u, s, v = linalg.svd(array1)
print(u.shape, s.shape, v.shape)
u, s, v = linalg.svd(array2)
print(u.shape, s.shape, v.shape)
u, s, v = linalg.svd(array3)
print(u.shape, s.shape, v.shape)
u, s, v = linalg.svd(array4)
print(u.shape, s.shape, v.shape)
奇异矩阵在这是奇异向量,该svd不只适用于numpy,也适用于torch,其实numpy和torch之间很多都是互通的。
(2)求范数 ( n u m p y . l i n a l g . n o r m ( d , o r d = 1 ) 可 任 意 s h a p e ) (numpy.linalg.norm(d, ord=1) 可任意shape) (numpy.linalg.norm(d,ord=1)可任意shape)
d为输入数组或张量(只能是一维或二维),ord为1代表求1-范数,ord为2代表求2-范数,不提供ord默认为求2-范数。
import numpy as np
import torch as tc
import numpy.linalg as linalg
array1 = np.random.randint(1, 10, size=(2, 3))
print(array1)
norm = linalg.norm(array1, ord=1)
print(norm)
norm = linalg.norm(array1, ord=2)
print(norm)
norm = linalg.norm(array1[0], ord=1)
print(norm)
norm = linalg.norm(array1[0], ord=2)
print(norm)
(3)求内积 n u m p y . v d o t ( 数 组 或 张 量 , 数 组 或 张 量 ) numpy.vdot(数组或张量,数组或张量) numpy.vdot(数组或张量,数组或张量)
支持任意shape求内积
import numpy as np
import torch as tc
array1 = np.random.randint(1, 10, size=(2, 3, 2, 2))
array4 = tc.randint(1, 10, size=(2, 3, 2, 2))
print(array1)
print(array4)
vdot = np.vdot(array1, array4)
print(vdot)
vdot = np.vdot(array1[:, :, :, 0], array4[:, :, :, 0])
print(vdot)
vdot = np.vdot(array1[:, :, 0], array4[:, :, 0])
print(vdot)
(4)求向量中所有元素的乘积 ( n u m p y . p r o d ) (numpy.prod) (numpy.prod)
支持numpy数组任意shape求所有元素的乘积,不能tensor类型。
import numpy as np
import torch as tc
array1 = np.random.randint(1, 10, size=(2, 2, 2, 2))
array4 = tc.randint(1, 10, size=(2, 2, 2))
print(array1)
print(np.prod(array1))
print(array4)
# 报错
# print(np.prod(array4))
(5)numpy简单计算 ( n u m p y . a b s 、 n u m p y . s q r t 、 n u m p y . m a x 、 n u m p y . m e a n 、 n u m p y . s t d 、 n u m p y . s u m ) (numpy.abs、numpy.sqrt、numpy.max、numpy.mean、numpy.std、numpy.sum) (numpy.abs、numpy.sqrt、numpy.max、numpy.mean、numpy.std、numpy.sum)
import numpy as np
array1 = np.random.randint(-6, 6, size=(3, 2))
print(np.abs(array1))
print(np.sqrt(abs(array1)))
# 均可指定维度:最大值、均值、标准差、总和
# 也可以直接对整体进行操作
print(np.max(array1))
print(np.mean(array1))
print(np.std(array1))
print(np.sum(array1))
print(np.max(array1, axis=1))
print(np.mean(array1, axis=1))
print(np.std(array1, axis=1))
print(np.sum(array1, axis=1))
(6)矩阵乘积和矩阵对应元素相乘 ( n u m p y . m a t m u l 、 n u m p y . m u l t i p l y ) (numpy.matmul、numpy.multiply) (numpy.matmul、numpy.multiply)
matmul支持两个矩阵相乘,维度不能超过二维,multiply支持任意相同shape的任意数量数组进行Hadamard乘积(对应位置元素相乘)
import numpy as np
array1 = np.random.randint(-6, 6, size=(3, 2))
print("array1:", array1)
print(np.matmul(array1, array1.T))
print(np.multiply(array1, array1, array1))
(7)共轭 ( n u m p y . c o n j ) (numpy.conj) (numpy.conj)
import numpy as np
array1 = np.random.randint(-6, 6, size=(3, 2)) + 2j
print(array1)
print(np.conj(array1))
(8)求迹(numpy.trace)
支持2维和3维数组求迹,3维数组实际上是批量求矩阵的迹然后放在一维数组中。
import numpy as np
array1 = np.random.randint(3, 6, size=(2, 3))
array2 = np.random.randint(3, 6, size=(2, 3, 6))
print(array1)
print(np.trace(array1))
print(array2)
print(np.trace(array2))
(9)爱因斯坦求和约定 ( n u m p y . e n i s u m ) (numpy.enisum) (numpy.enisum)
enisum可以完成前面提到的大部分操作,只要对提供的数组用字母进行了标记。建议在指定subscripts时显式指定,即使用’->’,因为这样易读。下面是一些基本的使用,可以看到该函数可以实现很多前面许多函数的功能。
import numpy as np
array1 = np.random.randint(3, 6, size=(2, 3))
array2 = np.random.randint(3, 6, size=(2, 3, 6))
array3 = np.random.randint(3, 6, size=(4, 4))
array4 = np.random.randint(3, 6, size=(4, 4, 5, 6, 7))
print("array1_shape:", array1.shape, "array2_shape:", array2.shape)
# 任意维度缩并
print("\n任意维度缩并:")
print(np.einsum("ij, ijl->l", array1, array2).shape)
# 任意维度外积
print("\n任意维度外积:")
print(np.einsum("ij, xyz->ijxyz", array1, array2).shape)
# hardmard积
print("\narray1:", array1)
print("array1求hardmard积:")
print(np.einsum('ij,ij->ij', array1, array1))
# 矩阵求迹
print("\narray3:", array3)
print("array3矩阵求迹:")
print(np.einsum(array3, [0, 0]))
# np.einsum("ii", array33)也可以求迹
# 求对角线上的元素
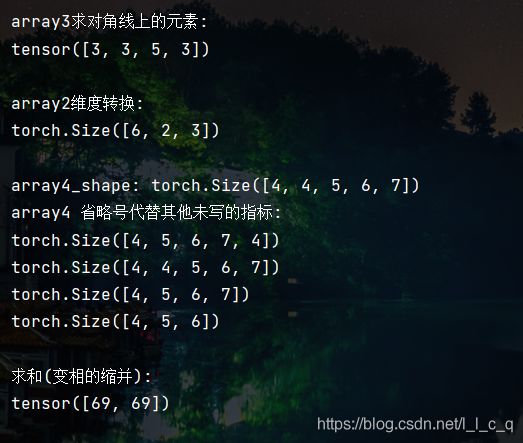
print("\narray3求对角线上的元素:")
print(np.einsum(array3, [0, 0], [0]))
# np.einsum('ii->i', array3)也可以求对角线上的元素
# 维度转换
print("\narray2维度转换:")
print(np.einsum("ijk->kij", array2).shape)
# 省略号
print("\narray4_shape:", array4.shape)
print("array4 省略号代替其他未写的指标:")
print(np.einsum("i...", array4).shape)
print(np.einsum("...i", array4).shape)
print(np.einsum("i...->...", array4).shape)
print(np.einsum("i...k->...", array4).shape)
# 求和(变相的缩并)
print("\n求和(变相的缩并):")
print(np.einsum("ijk->i", array2))
二.torch \textbf{二.torch} 二.torch
1.创建张量
(1)生成全1张量 ( t o r c h . o n e s ) (torch.ones) (torch.ones)
import torch as tc
tensor = tc.ones(size=(2, 3, 4, 5))
(2)生成全0张量 ( t o r c h . z e r o s ) (torch.zeros) (torch.zeros)
import torch as tc
tensor = tc.zeros(size=(2, 3, 4, 5))
(3)生成空张量 ( t o r c h . e m p t y ) (torch.empty) (torch.empty)
import torch as tc
tensor = tc.empty(size=(2, 3, 4, 5))
(4)生成一维均匀分布张量 ( t o r c h . l i n s p a c e ) (torch.linspace) (torch.linspace)
与numpy.linspace等效。
import torch as tc
import numpy as np
tensor = tc.linspace(start=0, end=20, steps=11)
array = np.linspace(start=0, stop=20, num=11)
print(tensor)
print(array)
(5)生成数值在一定范围内的整型张量 ( t o r c h . r a n d i n t ) (torch.randint) (torch.randint)
1可取,20不可取。
import torch as tc
tensor = tc.randint(low=1, high=20, size=(2, 3, 4))
print(tensor)
(6)将列表或数组强制转换为torch tensor ( t o r c h . t e n s o r ) (torch.tensor) (torch.tensor)
默认转换为浮点数张量,可强制转换为整型。
import torch as tc
import numpy as np
array = np.random.randint(low=1, high=20, size=(2, 3, 4))
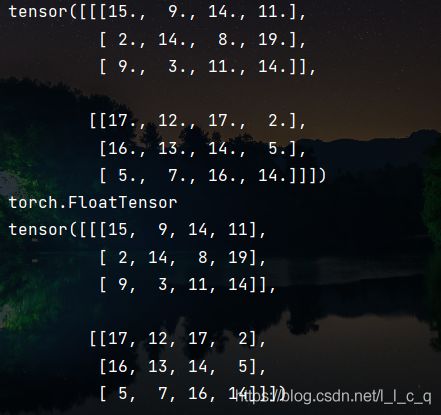
print(tc.Tensor(array))
print(tc.Tensor(array).type())
print(tc.Tensor(array).long())
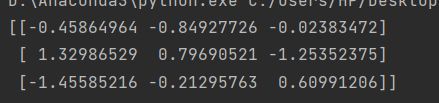
(7)返回一个符合均值为0,方差为1的正态分布(标准正态分布)中填充随机数的张量 ( t o r c h . r a n d n ) (torch.randn) (torch.randn)
import torch as tc
tensor = tc.randn(size=[4, 4])
print(tensor)
2.常用张量操作
(1)张量转置和维度转换 ( t e n s o r . t ( ) 、 t e n s o r . p e r m u t e ) (tensor.t()、tensor.permute) (tensor.t()、tensor.permute)
前者只支持二维张量,后者支持任意shape的张量。
import torch as tc
tensor = tc.randn(size=[4, 3])
print(tensor.t().shape)
tensor1 = tc.randn(size=[2, 3, 4])
print(tensor1.permute([0, 2, 1]).shape)
(2)改变shape ( t o r c h . r e s h a p e ) (torch.reshape) (torch.reshape)
import torch as tc
tensor1 = tc.randn(size=[2, 3, 4])
print(tc.reshape(tensor1, shape=(6, 4)).shape)
(3)张量拼接 ( t o r c h . c a t ) (torch.cat) (torch.cat)
支持任意shape的张量拼接,唯一要求是要拼接的维度以外的所有维度必须一致
import torch as tc
tensor1 = tc.randn(size=[2, 3, 4])
tensor2 = tc.randn(size=[4, 3, 4])
print(tc.cat((tensor1, tensor2), dim=0).shape)
(4)张量拷贝 ( t e n s o r A . c o p y ( t e n s o r B ) ) (tensorA.copy_(tensorB)) (tensorA.copy(tensorB))
import torch as tc
tensor1 = tc.randn(size=[2, 3])
tensor2 = tc.randn(size=[2, 3])
print(tensor1, tensor2)
tensor2.copy_(tensor1)
print(tensor1 == tensor2)

但这有一个小问题,就是不能直接tensor2.copy_(tensor1),而是需要预先定义好才可以这么用,可以使用detach来解决这个问题。
import torch as tc
tensor1 = tc.randn(size=[2, 3])
tensor2 = tc.detach(tensor1)
print(tensor2==tensor1)
(5)获取张量shape ( t e n s o r . s h a p e 、 t e n s o r . s i z e ( ) ) (tensor.shape、tensor.size()) (tensor.shape、tensor.size())
import torch as tc
tensor1 = tc.randn(size=[2, 3])
print(tensor1.shape, tensor1.size())
(6)
3.张量计算
(1)缩并 ( t o r c h . t e n s o r d o t ) (torch.tensordot) (torch.tensordot)
支持任意维度的缩并操作,且可以多缩并。dims提供的第一个列表是tensor2要缩并的维度,第二个列表是tensor1要缩并的维度
import torch as tc
tensor1 = tc.randint(low=1, high=5, size=[2, 2, 4, 5])
tensor2 = tc.randint(low=1, high=5, size=[3, 2])
result = tc.tensordot(tensor2, tensor1, dims=([1], [0]))
print(result.shape)
import torch as tc
tensor1 = tc.randint(low=1, high=5, size=[2, 2, 4, 5])
tensor2 = tc.randint(low=1, high=5, size=[3, 2, 2])
result = tc.tensordot(tensor2, tensor1, dims=([1, 2], [0, 1]))
print(result.shape)
(2)hadmard积实现对应元素相乘 ( ∗ ) (*) (∗)
import torch as tc
tensor1 = tc.randint(low=1, high=5, size=[2, 2])
tensor2 = tc.randint(low=1, high=5, size=[2, 2])
result = tensor2 * tensor1
print(tensor2, tensor1)
print(result)
print(result.shape)
(3)矩阵乘积 ( @ ) (@) (@)
@左边的张量的最后一个维度的维数需要与右边张量的第一个维度的维数相同,尽量都使用二维张量或其中一个是二维张量,不然容易出错,因为针对非二维张量,在矩阵乘积前会先将其reshape为二维张量,对于高阶的,使用tensordot更稳妥,且易读。
import torch as tc
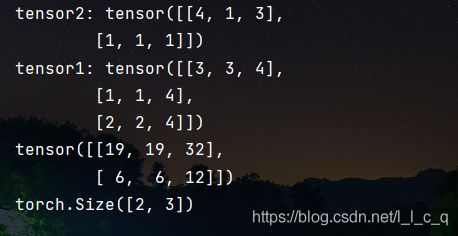
tensor1 = tc.randint(low=1, high=5, size=[3, 3])
tensor2 = tc.randint(low=1, high=5, size=[2, 3])
result = tensor2 @ tensor1
print("tensor2:", tensor2, "\ntensor1:", tensor1)
print(result)
print(result.shape)
(4)张量除法 ( t o r c h . f l o o r d i v i d e 、 t o r c h . t r u e d i v i d e ) (torch.floor_divide、torch.true_divide) (torch.floordivide、torch.truedivide)
import torch as tc
tensor1 = tc.randint(low=1, high=5, size=[3, 3])
result = tc.floor_divide(tensor1, 2)
r = tensor1 // 2
print(result == r)
result = tc.true_divide(tensor1, 2)
r = tensor1 / 2
print(result == r)

这两个函数与//和/似乎并无区别,由于过得有点久了,具体忘记为什么要用这两个函数了,反正如果//和/不好用就用这两个函数。
(5)爱因斯坦求和约定 ( t c . e i n s u m ) (tc.einsum) (tc.einsum)
和numpy的差不多,我只是对原来的代码做出了一点点修改就可以使用了。
import torch as tc
tensor1 = tc.randint(3, 6, size=(2, 3))
tensor2 = tc.randint(3, 6, size=(2, 3, 6))
tensor3 = tc.randint(3, 6, size=(4, 4))
tensor4 = tc.randint(3, 6, size=(4, 4, 5, 6, 7))
print("tensor1_shape:", tensor1.shape, "tensor2_shape:", tensor2.shape)
# 任意维度缩并
print("\n任意维度缩并:")
print(tc.einsum("ij, ijl->l", tensor1, tensor2).shape)
# 任意维度外积
print("\n任意维度外积:")
print(tc.einsum("ij, xyz->ijxyz", tensor1, tensor2).shape)
# hardmard积
print("\ntensor1:", tensor1)
print("tensor1求hardmard积:")
print(tc.einsum('ij,ij->ij', tensor1, tensor1))
# 矩阵求迹
print("\ntensor3:", tensor3)
print("tensor3矩阵求迹:")
print(tc.einsum("ii", tensor3))
# 求对角线上的元素
print("\ntensor3求对角线上的元素:")
print(tc.einsum('ii->i', tensor3))
# 维度转换
print("\ntensor2维度转换:")
print(tc.einsum("ijk->kij", tensor2).shape)
# 省略号
print("\ntensor4_shape:", tensor4.shape)
print("tensor4 省略号代替其他未写的指标:")
print(tc.einsum("i...", tensor4).shape)
print(tc.einsum("...i", tensor4).shape)
print(tc.einsum("i...->...", tensor4).shape)
print(tc.einsum("i...k->...", tensor4).shape)
# 求和(变相的缩并)
print("\n求和(变相的缩并):")
print(tc.einsum("ijk->i", tensor2))
(6)其他的一些计算
matmul支持两个矩阵相乘,维度不能超过二维,multiply支持任意相同shape的2个张量进行Hadamard乘积(对应位置元素相乘),而且可以注意到,torch相比numpy有着更严格的类型要求。
import torch as tc
tensor1 = tc.randint(low=-6, high=6, size=(3, 2))
print("abs,sqrt:")
print(tc.abs(tensor1))
print(tc.sqrt(abs(tensor1)))
# 均可指定维度:最大值、均值、标准差、总和
# 也可以直接对整体进行操作
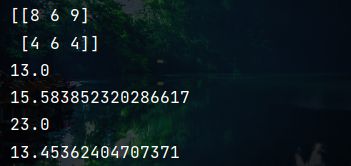
print("max,mean,std,sum:")
print(tc.max(tensor1))
print(tc.mean(tensor1.float()))
print(tc.std(tensor1.float()))
print(tc.sum(tensor1))
print(tc.max(tensor1, dim=1))
print(tc.mean(tensor1.float(), dim=1))
print(tc.std(tensor1.float(), dim=1))
print(tc.sum(tensor1, dim=1))
# 矩阵乘积和hardmard积
print("矩阵乘积和hardmard积")
print("tensor1:", tensor1)
print(tc.matmul(tensor1, tensor1.T))
print(tc.multiply(tensor1, tensor1))
print("共轭:")
tensor1 = tc.randint(-6, 6, size=(3, 2)) + 2j
print(tensor1)
print(tc.conj(tensor1))
4.数据类型强制转换
在需要进行数据类型转换的张量后加上.type(),比如t.long(),这就将张量t的数据类型强制转换为long型,还有double、int、float等等,相比在生成张量中提供dtype参数,这更加方便,想什么时候用就什么时候用。
三.拓展 \textbf{三.拓展} 三.拓展:
(1)tensor与numpy之间的转换
将numpy数组a转换为tensor
b=torch.from_numpy(a)
将tensor转换为numpy数组
b = a.numpy()
(2)ncon.ncon
这个函数与函数einsum的区别主要在于把字母换成了数字,是很类似的。
import numpy as np
from numpy import linalg as LA
from ncon import ncon
# 初始化张量
d = 2
chi = 10
# 10*2*10
A = np.random.rand(chi, d, chi)
B = np.random.rand(chi, d, chi)
# 设置辅助指标,两种辅助指标,分别是Sab和Sba
# 10
sAB = np.ones(chi) / np.sqrt(chi)
sBA = np.ones(chi) / np.sqrt(chi)
# 10*10
sigBA = np.random.rand(chi, chi)
tol = 1e-10
# 初始化张量网络
# 10*10 10*10 10*2*10 10*2*10 10*10 10*10 10*2*10 10*2*10
tensors = [np.diag(sBA), np.diag(sBA), A, A.conj(), np.diag(sAB),
np.diag(sAB), B, B.conj()]
labels = [[1, 2], [1, 3], [2, 4], [3, 5, 6], [4, 5, 7], [6, 8], [7, 9], [8, 10, -1], [9, 10, -2]]
# 10*10 10*10 10*10 10*2*10 10*2*10 10*10 10*10 10*2*10 10*2*10
sigBA_new = ncon([sigBA, *tensors], labels)
print(sigBA_new.shape)
(3)torch还可以用于深度学习(这一部分之后就可以不用看了,没有整理完,且短期可能不会再对其进行整理)
优化器
-
梯度下降:
梯度下降BGD全局最优
随机梯度下降SGD ( t o r c h . o p t i m . S G D ) (torch.optim.SGD) (torch.optim.SGD)
小批量梯度下降MBGD 找一批数据计算梯度,使用均值更新参数 -
动量法(Momentum优化器):
对网络梯度进行平滑处理,让梯度摆动幅度变得更小 -
AdaGrad ( t o r c h . o p t i m . A d a G r a d ) (torch.optim.AdaGrad) (torch.optim.AdaGrad):
自适应学习率 -
RMSProp ( t o r c h . o p t i m . R M S p r o p ) (torch.optim.RMSprop) (torch.optim.RMSprop):
对学习率加权,进一步优化梯度摆动幅度过大的问题,并进一步加速损失函数的收敛速度 -
Adam ( t o r c h . o p t i m . A d a m ) (torch.optim.Adam) (torch.optim.Adam):
Momentum和RMSProp的结合 torch.optim.Adam
损失函数(目前的理解是只要开启求导,使其可以反向传播即可)
- t o r c h . n n . B C E L o s s torch.nn.BCELoss torch.nn.BCELoss
ℓ ( x , y ) = L = { l 1 , … , l N } ⊤ , l n = − w n [ y n ⋅ log x n + ( 1 − y n ) ⋅ log ( 1 − x n ) ] \ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_n \left[ y_n \cdot \log x_n + (1 - y_n) \cdot \log (1 - x_n) \right] ℓ(x,y)=L={l1,…,lN}⊤,ln=−wn[yn⋅logxn+(1−yn)⋅log(1−xn)] - t o r c h . n n . N L L L o s s torch.nn.NLLLoss torch.nn.NLLLoss
- t o r c h . n n . M S E L o s s torch.nn.MSELoss torch.nn.MSELoss
# MSELoss均方误差,常用语分类
loss_fn = torch.nn.MSELoss()
loss = loss_fn(y_true, y_predict)
- t o r c h . n n . C r o s s E n t r o p y L o s s torch.nn.CrossEntropyLoss torch.nn.CrossEntropyLoss
# 交叉熵损失,常用语逻辑回归
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(input,target)
- 自 定 义 损 失 函 数 自定义损失函数 自定义损失函数
激活函数
- t o r c h . n n . S i g m o i d torch.nn.Sigmoid torch.nn.Sigmoid
- t o r c h . n n . R e L U torch.nn.ReLU torch.nn.ReLU
- t o r c h . n n . T a n h torch.nn.Tanh torch.nn.Tanh
- t o r c h . n n . S o f t m a x torch.nn.Softmax torch.nn.Softmax
- 自 定 义 激 活 函 数 自定义激活函数 自定义激活函数
已经封装好的层和模型(下面仅列出几个)
- t o r c h . n n . L i n e a r torch.nn.Linear torch.nn.Linear
- t o r c h . n n . C o n v 2 d torch.nn.Conv2d torch.nn.Conv2d
- t o r c h . n n . M a x P o o l 2 d torch.nn.MaxPool2d torch.nn.MaxPool2d
- t o r c h . n n . E m b e d d i n g torch.nn.Embedding torch.nn.Embedding
- t o r c h . n n . torch.nn. torch.nn.
- 自 定 义 层 和 模 型 自定义层和模型 自定义层和模型