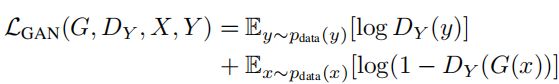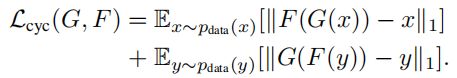cycleGAN解析
前言
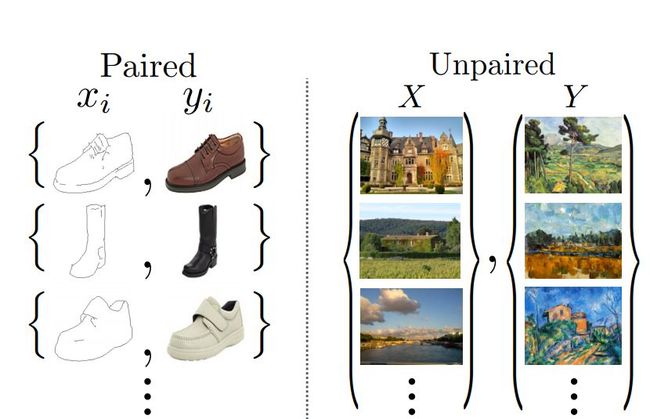
在上一篇博文中我们讲述了pix2pix的方法，见Pix2Pix原理解析，pix2pix的方法适用于成对数据的风格迁移，如下图左边。但是在大多数情况，对于A风格的图像，我们并没有与之相对应的B风格图像，我们所拥有的是一群处于风格A（源域）的图像和一群处于风格B（目标域）的图像，这样pix2pix2的方法就不管用了。CycleGAN的创新点在于能够在源域和目标域之间，无须建立训练数据间一对一的映射，就可实现这种迁移。这个方法的提出时间为2017年，目前来说是非常经典和基本的方法。
论文地址：https://arxiv.org/abs/1703.10593
基本架构
cyclegan的原理如下图所示。整个架构结构整理如下：
（1） 输入：
- x：源域，风格A的图像
- y：目标域，风格B的图像
（2）两个生成器：
- G：用于将风格A的图像x转换为风格B的图像
- F：用于将风格B的图像y转换为风格A的图像
所谓的cycle，可以理解为：
- 通过G将风格A的图像x转换为风格B的图像
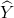，之后再将通过F后仍然能转换回风格A，并能保证图像中的内容一致。 - 通过F将风格B的图像y转换为风格A的图像
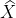，之后再将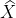通过G后仍然能转换回风格B，并能保证图像中的内容一致。
也就是训练好G和F就可以自由地完成风格A、B的转换了。
损失函数
在训练中我们引入了两个判别器：
- Dy：区分真实的风格B的图像与通过G转换而来的假的风格B图像
- Dx：区分真实的风格A的图像与通过G转换而来的假的风格B图像
损失函数主要由以下几个部分构成：
（1）Dy处的GAN损失：
（2）Dx处的GAN损失：
（3）循环一致性损失，即我们前面所述的cycle缘由：
（4）Identity loss
这个loss实在代码中实现才发现的。它的含义是生成器G用来生成y风格图像，那么把y送入G，应该仍然生成y，只有这样才能证明G具有生成y风格的能力。因此G(y)和y应该尽可能接近。根据论文中的解释，如果不加该loss，那么生成器可能会自主地修改图像的色调，使得整体的颜色产生变化。
代码
采用官方实现的pytorch代码：https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix
（1）向前传播部分：
- netG_A就是G，完成A->B的风格转换（源域到目标域）
- netG_B就是F，完成B->A的风格转换（目标域到源域）
def forward(self):
"""Run forward pass; called by both functions and ."""
self.fake_B = self.netG_A(self.real_A) # G_A(A)
self.rec_A = self.netG_B(self.fake_B) # G_B(G_A(A))
self.fake_A = self.netG_B(self.real_B) # G_B(B)
self.rec_B = self.netG_A(self.fake_A) # G_A(G_B(B)) （2）更新G：
在if lambda_idt > 0:这个分支内，实现的就是Identity loss。
后面就是Gan损失（loss_G_A、loss_G_B）以及循环一致性损失（loss_cycle_A、loss_cycle_B）
注意：代码里面的判别器netD_A判断的是真实B风格和生成B风格的真假（相当于论文中Dy）
同理netD_B判断的是真实A风格和生成A风格的真假（相当于论文中Dx）
def backward_G(self):
"""Calculate the loss for generators G_A and G_B"""
lambda_idt = self.opt.lambda_identity
lambda_A = self.opt.lambda_A
lambda_B = self.opt.lambda_B
# Identity loss
if lambda_idt > 0:
# G_A should be identity if real_B is fed: ||G_A(B) - B||
self.idt_A = self.netG_A(self.real_B) #将真实的B送入netG_A(A->B风格生成器)生成的应该还是B风格
self.loss_idt_A = self.criterionIdt(self.idt_A, self.real_B) * lambda_B * lambda_idt
# G_B should be identity if real_A is fed: ||G_B(A) - A||
self.idt_B = self.netG_B(self.real_A) #将真实的A送入netG_B(B->A风格生成器)生成的应该还是A风格
self.loss_idt_B = self.criterionIdt(self.idt_B, self.real_A) * lambda_A * lambda_idt
else:
self.loss_idt_A = 0
self.loss_idt_B = 0
# GAN loss D_A(G_A(A))
self.loss_G_A = self.criterionGAN(self.netD_A(self.fake_B), True)
# GAN loss D_B(G_B(B))
self.loss_G_B = self.criterionGAN(self.netD_B(self.fake_A), True)
# Forward cycle loss || G_B(G_A(A)) - A||
self.loss_cycle_A = self.criterionCycle(self.rec_A, self.real_A) * lambda_A
# Backward cycle loss || G_A(G_B(B)) - B||
self.loss_cycle_B = self.criterionCycle(self.rec_B, self.real_B) * lambda_B
# combined loss and calculate gradients
self.loss_G = self.loss_G_A + self.loss_G_B + self.loss_cycle_A + self.loss_cycle_B + self.loss_idt_A + self.loss_idt_B
self.loss_G.backward()（3）更新D：
def backward_D_A(self):
"""Calculate GAN loss for discriminator D_A"""
fake_B = self.fake_B_pool.query(self.fake_B)
self.loss_D_A = self.backward_D_basic(self.netD_A, self.real_B, fake_B)
def backward_D_B(self):
"""Calculate GAN loss for discriminator D_B"""
fake_A = self.fake_A_pool.query(self.fake_A)
self.loss_D_B = self.backward_D_basic(self.netD_B, self.real_A, fake_A)
生成器结构
最后再补充一下cyclegan所采用的生成器的结构，是来来自于论文：Perceptual Losses for Real-Time Style Transfer and Super-Resolution，有兴趣大家可以搜索一下，基本结构如下。
一共是由3个卷积层、5个残差块、3个卷积层构成。
这里没有用到池化等操作进行采用，在开始卷积层中（第二层、第三层）进行了下采样，在最后的3个卷积层中进行了上采样，这样最直接的就是减少了计算复杂度，另外还有一个好处是有效受区域变大，卷积下采样都会增大有效区域。5个残差块都是使用相同个数的（128）滤镜核，每个残差块中都有2个卷积层（3*3核），这里的卷积层中没有进行标准的0填充（padding），因为使用0填充会使生成出的图像的边界出现严重伪影。为了保证输入输出图像大小不改变，在图像初始输入部分加入了反射填充。
这里的残差网络不是使用何凯明的残差网络（卷积之后没有Relu），而是使用了Gross and Wilber的残差网络 。后面这种方法验证在图像分类算法上面效果比较好。
对于输入是256×256大小的图像，residual block共有9个，对于128×128大小的图像，residual block为6个.
