神经辐射场 3D 重建——NeRF

NeRF（ECCV 2020）主要贡献：

1. 提出一种将具有复杂几何性质和材料的连续场景表示为 5D 神经辐射场的方法，并将其参数化为基本的 MLP 网络
2. 提出一种基于经典体渲染技术的可微渲染方式，论文用它来优化标准 RGB 图像的表示
3. 提出位置编码将每个输入 5D 坐标映射到高维空间，这使得论文能够成功优化神经辐射场来表示高频场景内容

前言

5D 坐标

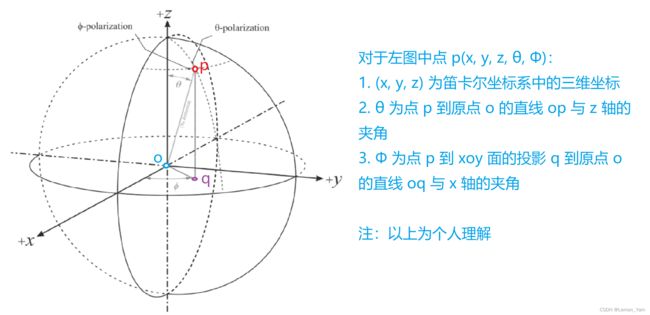
论文提出了一种通过使用稀疏的输入图像集优化底层连续体积场景函数（volumetric scene function）的方法，从而达到了合成复杂场景新视图的 SOTA。论文的算法使用全连接深度网络表示场景，网络的输入是包括3D 位置信息 $(x,y,z)$ 和视角方向 $(\theta ,\varphi )$ 的单个连续的 5D 坐标，其输出是该空间位置的体积密度 $\sigma$ 和与视图相关的 RGB 颜色，接着使用经典的体绘制技术将输出的颜色和密度投影到图像中。优化合成新视图所需要的唯一输入是一组具有已知相机位姿的图像（NeRF 中的 lego 小车使用 100 张图像），而 5D 坐标是通过沿着对应像素的相机光线采样所得到的。

坐标变换

三种坐标系：

1. 世界坐标系：表示物理上的三维世界
2. 相机坐标系：表示虚拟的三维相机坐标
3. 图像坐标系：表示二维的图片坐标

相机坐标 $(X_c,Y_c,Z_c{)}^T$ 和世界坐标 $(X,Y,Z{)}^T$ 之间存在如下转换关系：
$$\begin{gathered} C_c=\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]=\left[\begin{array}{cccc}Co{l}_1& Co{l}_2& Co{l}_3& C_t\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]=M_{w2c}{C}_w \\ Co{l}_i=[r_{1i},r_{2i},r_{3i}{]}^T,i\in [1,2,3]C_t=[t_x,t_y,t_z{]}^T \end{gathered}$$
✍️其中，矩阵 $M_{w2c}$ 是一个仿射变换矩阵，也可叫做相机的外参矩阵；$[Co{l}_1,Co{l}_2,Co{l}_3]$ 包含旋转信息；$C_t$ 包含平移信息。

对于二维图片的坐标 $[x,y{]}^T$ 和相机坐标系下的坐标 $[U,V,W]$ 存在如下转换关系：
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}U\\ V\\ W\end{array}\right]=M_{c2i}{C}_c$$
✍️其中，矩阵 $M_{c2i}$ 为相机的内参矩阵（透视投影矩阵），包含焦距 $(f_x,f_y)$ 以及图像中心点的坐标 $(c_x,c_y)$。

论文使用数据集的配置文件 *.json 中的 transform_matrix 为上面所述仿射变换矩阵 $M_{w2c}$ 的逆矩阵 $M_{c2w}=M_{w2c}^{-1}$；而 camera_angle_x 是相机的水平视场 (horizontal field of view)，可以用于算焦距。

常见图像质量评估指标

• 结构相似性 SSIM：一种衡量两幅图像相似度的指标，其值越大则两张图片越相似（范围为 $[0,1]$）。给定两张图片 $x$ 和 $y$，其计算公式如下：

$$SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}$$

✍️其中，${\mu }_x$ 为 $x$ 的均值，${\mu }_y$ 为 $y$ 的均值，${\sigma }_x$ 为 $x$ 的方差，${\sigma }_y$ 为 $y$ 的方差，${\sigma }_{xy}$ 为 $x$ 和 $y$ 的协方差，$c_1=(K_{1}L{)}^2$，$c_2=(K_{2}L{)}^2$，$K_1=0.01$，$K_2=0.03$，$L$ 为像素值的动态范围（如 255）。

• 峰值信噪比 PSNR：一般用于衡量最大值信号和背景噪音之间的图像质量参考值，其值越大图像失真越少（单位为 dB）。一般来说，PSNR 高于 40dB 说明图像质量几乎与原图一样好；在 30-40dB 之间通常表示图像质量的失真损失在可接受范围内；在 20-30dB 之间说明图像质量比较差；PSNR 低于 20dB 说明图像失真严重。给定一个大小为 $m\times n$ 的原始图像 I 和带噪声的图像 K，首先需要计算这两张图像的均方误差 MSE，接着再通过 MSE 计算峰值信噪比 PSNR，其计算公式如下：

$$\begin{array}{rl}MSE& =\frac{1}{mn}\sum _{i=0}^{m-1}\sum _{j=0}^{n-1}[I(i,j)-K(i,j){]}^2\\ PSNR& =10\cdot {\log }_{10}(\frac{MA{X}_I^2}{MSE})\end{array}$$

✍️其中，$MA{X}_I$ 为图像 I 可能的最大像素值，$I(i,j)$ 和 $K(i,j)$ 分别为图像 I 和 K 对应位置 $(i,j)$ 的像素值。

• 学习感知图像块相似度 LPIPS：用于计算参考图像块 $x$ 和失真图像块 $x_0$ 之间的距离，其值越小则相似度越高。LPIPS 先提取特征并在通道维度中进行单元归一化，对于 $l$ 层，我们将得到的结果记为 ${\hat{y}}^l$，${\hat{y}}_0^l\in {\mathcal{R}}^{H_l\times H_l\times C_l}$。接着，再利用向量 $w_l\in {\mathcal{R}}^{C_l}$ 缩放激活通道并计算 $l_2$ 距离，最后在空间上求平均值，在信道上求和。其公式如下：

$$d(x,x_0)=\sum _l\frac{1}{H_l{W}_l}\sum _{h,w}\parallel w_l⨀({\hat{y}}_{hw}^l-{\hat{y}}_{0hw}^l){\parallel }_2^2$$

✍️若对该指标的细节感兴趣，可参考这篇文章。

网络结构

神经辐射场 NeRF 是 Neural Radiance Fields 的缩写，其可以简要概括为用一个 MLP 神经网络去隐式地学习一个静态 3D 场景。为了训练网络，针对一个静态场景，需要提供大量相机参数已知的图片。基于这些图片训练好的神经网络，即可以从任意角度渲染出图片的结果。以下为 NeRF 的总体框架：

1. 获取采样点的 5D 坐标 $(xx,dd)$ ，该坐标包含 3D 位置信息 $xx=(x,y,z)$ 和视角方向 $dd=(\theta ,\varphi )$。
2. 通过位置编码对 3D 位置 $xx\in {\mathcal{R}}^3$ 和视角方向 $dd\in {\mathcal{R}}^2$ 进行相应处理，从而得到编码后的信息 $\gamma (xx)\in {\mathcal{R}}^{60}$ 和 $\gamma (dd)\in {\mathcal{R}}^{24}$。对于编码后的维度可参考后面位置编码章节做理解。
3. 将 $\gamma (xx)$ 输入到 8 层全连接层中，每层通道数为 256 且都经过 ReLU 函数激活（黑色实箭头）。此外，论文还遵循 DeepSDF 架构，将通过一个跳连接将输入 $\gamma (xx)$ 拼接到第 5 个全连接层的输出中。
4. 在第 8 个全连接层后添加一个新的全连接层，该层通道数为 256 且不经过激活函数（橙色箭头）。其输出为维度 256 的中间特征 $F_t$ 和体素密度 $\sigma$（可近似理解为不透明度，值越小越透明）。对于 $\sigma$，论文通过激活函数 ReLU 来确保其为非负的。
5. 将编码后的视角方向 $\gamma (dd)$ 和中间特征 $F_t$ 拼接起来，然后送入输出通道数为 128 的全连接层中，再经过激活函数 ReLU 处理得到特征 $F_c$。
6. 将 $F_c$ 送入全连接层中，再经过 sigmoid 激活函数（黑色虚箭头）处理得到三维的 RGB 输出。
7. 通过体渲染技术利用上面输出的颜色和体密度来合成图像。由于渲染函数是可微的，所以可以通过最小化合成图像与真实图像之间的误差（residual）来优化场景表示。

✍️NeRF 中输出 $\sigma$ 只与位置有关，而颜色 RGB 还与视角方向相关。

体渲染

体密度 $\sigma (xx)$ 可解释为射线在 $xx$ 位置终止于无穷小的粒子的微分概率（简单理解为不透明度），而相机射线 $rr(t)=oo+tdd$ 的期望颜色 $C(r)$ 在近界 $t_n$ 和远界 $t_f$ 下为：
$$C(rr)={\int }_{t_n}^{t_f}T(t)\sigma (rr(t))cc(rr(t),dd)dt,whereT(t)=exp(-{\int }_{t_n}^t\sigma (rr(s))ds)(1)$$

✍️函数 $T(t)$ 表示射线从 $t_n$ 到 $t$ 沿射线累积透射率，即射线从 $t_n$ 到 $t$ 不碰到其他任何粒子（particle）的概率。前面累积的体积密度 ${\int }_{t_n}^t\sigma (rr(s))ds$ 越大（非负），则 $T(t)$ 越小，从而降低（因为遮挡）该位置对颜色的影响：当前区域体积密度 $\sigma (rr(t))$ 越高，对颜色影响越大，但其会降低后面区域对颜色的影响（例如前面区域完全不透明，那么后面区域不管什么颜色，都不会影响该方向物体的颜色）。因此，这里根据 $T(t)$ 来降低相应区域对颜色的影响。

通过对所需虚拟相机（virtual camera）的每个像素的光线计算这个积分 $C(r)$ 来为连续的神经辐射场绘制视图，从而得到颜色值。论文用求积法对这个连续积分进行数值估计，而确定性求积（deterministic quadrature）通常用于绘制离散体素网格。因为 MLP 只会在一些固定的离散位置集上执行，所以它会有限制表示的分辨率（representation’s resolution）。相反，论文采用分段抽样方法（stratified sampling），将 $[t_n,t_f]$ 划分为 $N$ 等分，然后从每一块中均匀随机（uniformly at random）抽取一个样本：
$$t_i\sim \mathcal{U}[t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)](2)$$
虽然论文使用离散的样本集来估计积分，但因为分段抽样会导致 MLP 在优化过程中的连续位置被评估，从而能够表示一个连续的场景。论文使用 Max 在体绘制综述中讨论的正交规则（quadrature rule）和这些离散的样本来估计 $C(r)$：
$$\hat{C}(rr)=\sum _{i=1}^N{T}_i(1-\exp (-{\sigma }_i{\delta }_i)){cc}_i,where{T}_i=\exp (-\sum _{j=1}^{i-1}{\sigma }_j{\delta }_j)(3)$$
✍️其中，${\delta }_i=t_{i+1}-t_i$ 为相邻两个采样点之间的距离。这个从 $({cc}_i,{\sigma }_i)$ 值集合计算 $\hat{C}(rr)$ 的函数是可微的。因此，基于这样的渲染方式就可以用 NeRF 函数从任意角度中渲染出图片。

位置编码

尽管神经网络是通用的函数近似器（universal function approximators），但其在表示颜色和几何形状方面的高频变化方面表现不佳，这表明深度网络偏向于学习低频函数。论文表明，在将输入传递给网络之前，使用高频函数将输入映射到更高维度的空间，可以更好地拟合包含高频变化的数据。 为了能有效提升清晰度，论文引入了位置编码，将位置信息映射到高频空间，从而将 MLP 表示为 $F_{\Theta }=F_{\Theta }^{{}^{\prime }}\circ \gamma$ ，位置编码 $\gamma$ 表达式如下：
$$\begin{array}{rl}\gamma (p)& =(\sin (2^0\pi p),\cos (2^0\pi p),\cdots ,\sin (2^{L-1}\pi p),\cos (2^{L-1}\pi p))(4)\end{array}$$
✍️其中，$F_{\Theta }^{{}^{\prime }}$ 仍然是一个 MLP，而 $\gamma$ 是从 $\mathbb{R}$ 维空间到高维空间 ${\mathbb{R}}^{2L}$ 的映射，$\gamma (\cdot )$ 分别应用于 $xx$ 中的三个坐标值（被归一化到 $[-1,1]$）和笛卡尔视角方向单位向量（Cartesian viewing direction unit vector） $dd$ 的三个分量（其范围为 $[-1,1]$）。计算 $\gamma (xx)$ 时 $L=10$， 即维度为 $3\times 2\times 10=60$；计算 $\gamma (dd)$ 时 $L=4$，即维度为 $3\times 2\times 4=24$。

多层级体素采样

NeRF 的渲染过程计算量很大，每条射线都要采样很多点。但实际上，一条射线上的大部分区域都是空区域，或者是被遮挡的区域，对最终的颜色没啥贡献，而原始方法会对这些区域重复取样，从而降低了效率。因此，论文引入多层级体素采样（ Hierarchical volume sampling），采用了一种 “coarse to fine" 的形式，同时优化 coarse 网络和 fine 网络。对于 coarse 网络，论文采样较为稀疏的 $N_c$ 个点，并将前述式子 (3) 的离散求和函数重新表示为：
$${\hat{C}}_c(rr)=\sum _{i=1}^{N_c}{w}_i{c}_i,w_i=T_i(1-\exp (-{\sigma }_i{\delta }_i))(5)$$
然后对权值做归一化： ${\hat{w}}_i=w_i/{\sum }_{j=1}^{N_c}{w}_j$ ，此处的 ${\hat{w}}_i$ 可以看作是沿着射线的概率密度函数（PDF），通过这个概率密度函数可以粗略地得到射线上物体的分布情况。接下来，基于得到的分布使用逆变换采样（inverse transform sampling）来采样 $N_f$ 个点，并用这 $N_f$ 个点和前面的 $N_c$ 个点通过前面公式 (3) 一同计算 fine 网络的渲染结果 ${\hat{C}}_f(rr)$。虽然 coarse to fine 是计算机视觉领域中常见的一个思路，但这篇论文中用 coarse 网络来生成概率密度函数，再基于概率密度函数采样更精细的点算的上是很有趣新颖的做法。采样的图示如下：

✍️上图中，白色的点为第一阶段采样的 $N_c$ 个点，而黄色的点为第二阶段根据 PDF 采样的 $N_f$ 个点。

损失函数

由于渲染函数是可微的，所以可以通过下式来计算损失：
$$\mathcal{L}=\sum _{rr\in \mathcal{R}}[\parallel {\hat{C}}_c(rr)-C(rr){\parallel }_2^2+\parallel {\hat{C}}_f(rr)-C(rr){\parallel }_2^2]$$

✍️其中 $\mathcal{R}$ 为每批射线的集合，$C(r)r)$、${\hat{C}}_c(rr)$、${\hat{C}}_f(rr)$ 分别为射线 $rr$ 的 ground truth、粗体积（coarse volume）预测、精体积（fine volume）预测的 RGB 颜色。虽然最终的渲染来自 ${\hat{C}}_f(rr)$，但也要同时最小化 ${\hat{C}}_c(rr)$ 的损失，从而使粗网络的权值分布可以用于细网络中的样本分配。

代码运行结果

以下是运行 200k 轮后生成的 lego 模型（显卡 RTX3060 6G，训练时间约 15h），代码使用 pytorch 版本（文末有附地址）

✍️在训练过程中，渲染时出现 GPU 内存不足，可通过减少 chunk 大小解决问题

# parser.add_argument("--chunk", type=int, default=1024*32, 
parser.add_argument("--chunk", type=int, default=1024*16, 
                    help='number of rays processed in parallel, decrease if running out of memory')

以下是消融实验的部分结果：

• 移除 View Dependence（即不使用视角方向 $dd$）会阻碍模型在推土机胎面上重新创建镜面反射（specular reflection）
• 移除位置编码大大降低了模型表示高频几何和纹理的能力，导致外观过平滑

pytorch 版 NeRF（速度比原始代码快大约 1.3 倍）：https://github.com/yenchenlin/nerf-pytorch

文章：https://arxiv.org/pdf/2003.08934.pdf

项目地址：https://www.matthewtancik.com/nerf

文章补充：【NeRF论文笔记】用于视图合成的神经辐射场技术、NeRF：用深度学习完成3D渲染任务的蹿红、NeRF论文阅读、【3D】NeRF论文随笔、【学习笔记】NeRF