大白羊_Aries

CS231n 课程（笔记内容 by Aries.Y）

图像分类

图像分类的任务，就是对于一个给定的图像，预测它属于的那个分类标签（或者给出属于一些列不同标签的可能性）

好的图像分类模型能够在维持分类结论稳定的同时，保持堆类间差异足够敏感

数据驱动的方法就是像教小孩子看图识物一样：给计算机很多数据，然后实现学习算法，让计算机学习到每个类的外形

图像分类的流程大致分为：

输入：输入是包含N个图像的集合，每个图像的标签是K种分类标签中的一种。这个集合称为训练集
学习：这一步的任务是使用训练集来学习每个类到底长什么样。一般该步骤叫做训练分类器或者学习一个模型
评价：让分类器来预测它未曾见过的图像的分类标签，并以此来评价分类器的质量。我们会把分类器预测的标签和图像真正的分类标签对比。毫无疑问，分类器预测的分类标签和图像真正的分类标签如果一致，那就是好事，这样的情况越多越好

Nearest Neighbor 分类器

假设我们对 CIFAR-10 进行最近邻分类

CIFAR-10 这个数据集包含了 60000 张 32x32 的小图像。每张图像都有 10 种分类标签中的一种。这 60000 张图像被分为包含 50000 张图像的训练集和包含 10000 张图像的测试集

于是，下面我们要做的事就是通过 Nearest Neighbor 算法将测试图片和训练集中每一张图片做比较，然后将它认为最相似的那个训练集图片的标签赋给这张测试图片

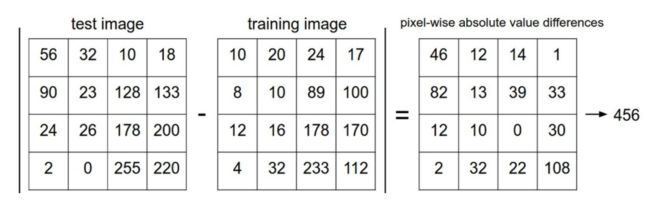
对于 CIFAR-10 就是比较 32x32x3 的像素块，最简单的方法就是逐个像素比较，最后将差异值全部加起来。换句话说，就是将两张图片先转化为两个向量 $I_1$ 和 $I_2$ ，然后计算他们的 『L1 距离』： $d_1(I_1,I_2) = \sum_p|I^p_1-I^p_2|$

这里的求和是针对所有的像素。下面是整个比较流程的图例

距离选择：计算向量间的距离有很多种方法，另一个常用的方法是 『L2距离』，从几何学的角度，可以理解为它在计算两个向量间的欧式距离。L2距离的公式如下： $d_2(I_1,I_2)=\sqrt{\sum_p(I^p_1-I^p_2)^2}$

关于 L1 和 L2 的一点比较： 在面对两个向量之间的差异时，L2 比 L1 更加不能容忍这些差异，也就是说，相对于一个巨大的差异， L2 距离更倾向于接受多个中等程度的差异

k-Nearest Neighbor 分类器

Nearest Neighbor 采用最相似的一张图片，显然这样做缺乏一定的合理性。于是，就出现了 k-Nearest Neighbor 分类器：与其只找最相近的那一张图片的标签，我们找最相似的 k 个图片的标签，然后让他们针对测试图片进行投票，最后把票数最高的标签作为对测试图片的预测

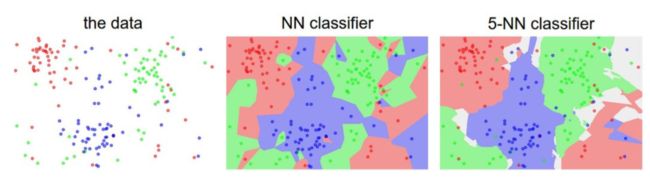
不同颜色区域代表的是使用L2距离的分类器的 『决策边界』。白色的区域是分类模糊的例子（即图像与两个以上的分类标签绑定）

需要注意的是，在 NN 分类器中，异常的数据点（比如：在蓝色区域中的绿点）制造出一个不正确预测的孤岛。5-NN 分类器将这些不规则都平滑了，使得它针对测试数据的泛化能力更好

用于超参数调优的验证集

k-NN 分类器需要设定 k 值，那么选择哪个 k 值最合适的呢？我们可以选择不同的距离函数，比如L1范数和L2范数等，那么选哪个好？还有不少选择我们甚至连考虑都没有考虑到（比如：点积）。所有这些选择，被称为 『超参数（hyperparameter）』

超参数有一个显著的特征就是它们的设置或取值并不是十分的显而易见，我们往往尝试不同的值，看哪个值表现最好就选哪个

为了设置超参数，我们引入了 『验证集』：从训练集中取出一部分数据用于调优

对于训练集、验证集和测试集，我们有如下的描述：
把训练集分成训练集和验证集。使用验证集来对所有超参数调优。最后只在测试集上跑一次并报告结果

有时候，训练集数量较小（因此验证集的数量更小），人们会使用一种被称为 『交叉验证』 的方法。例如，将训练集平均分成 5 份，其中 4 份用来训练，1 份用来验证。然后我们循环着取其中 4 份来训练，其中 1 份来验证，最后取所有5次验证结果的平均值作为算法验证结果

在实际情况下，人们不是很喜欢用交叉验证，主要是因为它会耗费较多的计算资源。一般直接把训练集按照 50%-90% 的比例分成训练集和验证集。但这也是根据具体情况来定的：如果超参数数量多，你可能就想用更大的验证集，而验证集的数量不够，那么最好还是用交叉验证吧。至于分成几份比较好，一般都是分成 3、5 和 10 份

给出训练集和测试集后，训练集一般会被均分。这里是分成 5 份。前面 4 份用来训练，黄色那份用作验证集调优。如果采取交叉验证，那就各份轮流作为验证集

Nearest Neighbor 分类器的优劣

Nearest Neighbor 分类器易于理解，实现简单。其次，算法的训练不需要花时间，因为其训练过程只是将训练集数据存储起来。然而测试要花费大量时间计算，因为每个测试图像需要和所有存储的训练图像进行比较，这显然是一个缺点。在实际应用中，我们关注测试效率远远高于训练效率。其实，我们后续要学习的卷积神经网络在这个权衡上走到了另一个极端：虽然训练花费很多时间，但是一旦训练完成，对新的测试数据进行分类非常快。这样的模式就符合实际使用需求

Nearest Neighbor 分类器的计算复杂度研究是一个活跃的研究领域，若干 Approximate Nearest Neighbor （ANN）算法和库的使用可以提升 Nearest Neighbor 分类器在数据上的计算速度（比如：FLANN）。这些算法可以在准确率和时空复杂度之间进行权衡，并通常依赖一个预处理/索引过程，这个过程中一般包含 kd 树的创建和 k-means 算法的运用

Nearest Neighbor 分类器在某些特定情况（比如数据维度较低）下，可能是不错的选择。但是在实际的图像分类工作中，很少使用。因为图像都是高维度数据（他们通常包含很多像素），而高维度向量之间的距离通常是反直觉的

从图像到标签分值的参数化映射

线性分类主要有两部分组成：一个是 『评分函数（score function）』，它是原始图像数据到类别分值的映射。另一个是 『损失函数（loss function）』，它是用来量化预测分类标签的得分与真实标签之间一致性的。该方法可转化为一个最优化问题，在最优化过程中，将通过更新评分函数的参数来最小化损失函数值

该方法的第一部分就是定义一个评分函数，这个函数将图像的像素值映射为各个分类类别的得分，得分高低代表图像属于该类别的可能性高低。下面会利用一个具体例子来展示该方法

现在假设有一个包含很多图像的训练集 $x_i\in R^D$ ，每个图像都有一个对应的分类标签 $y_i$ ，这里 $i=1,2,\cdots,N$ 并且 $y_i\in1,2,\cdots,K$ ，这就是说，我们有 $N$ 个图像样例，每个图像的维度是 $D$ ，共有 $K$ 种不同的分类

举例来说，在 CIFAR-10 中，我们有一个 $N = 50000$ 的训练集，每个图像有 $D=32\times32\times3=3072$ 个像素，而 $K = 10$ ，这是因为图片被分为10个不同的类别

我们现在定义评分函数为： $f:R^D\rightarrow R^K$ ，该函数是原始图像像素到分类分值的映射

在线性分类模型中，我们从最简单的概率函数开始，一个线性映射： $f(x_i, W, b) = Wx_i+b$

在上面的公式中，假设每个图像数据都被拉长为一个长度为 $D$ 的列向量，大小为 $\times 1]$ ，其中大小为 $\times D]$ 的矩阵 $W$ 和大小为 $\times 1]$ 列向量 $b$ 为该函数的参数

还是以CIFAR-10为例， $x_i$ 就包含了第 $i$ 个图像的所有像素信息，这些信息被拉成为一个 $3072 \times 1]$ 的列向量， $W$ 大小为 $10 \times 3072]$ ， $b$ 的大小为 $[10\times1]$ 。因此，3072 个数字（原始像素数值）输入函数，函数输出 10 个数字（不同分类得到的分值）。参数 $W$ 被称为 『权重（weights）』， $b$ 被称为 『偏差向量（bias vector）』，这是因为它影响输出数值，但是并不和原始数据 $x_i$ 产生关联

需要注意的几点：

首先，一个单独的矩阵乘法 $Wx_i$ 就高效地并行评估 10 个不同的分类器（每个分类器针对一个分类），其中每个类的分类器就是 $W$ 的一个行向量
注意我们认为输入数据 $x_i,y_i)$ 是给定且不可改变的，但参数 $W$ 和 $b$ 是可控制改变的。我们的目标就是通过设置这些参数，使得计算出来的分类分值情况和训练集中图像数据的真实类别标签相符
该方法的一个优势是训练数据是用来学习到参数 $W$ 和 $b$ 的，一旦训练完成，训练数据就可以丢弃，留下学习到的参数即可。这是因为一个测试图像可以简单地输入函数，并基于计算出的分类分值来进行分类
最后，注意只需要做一个矩阵乘法和一个矩阵加法就能对一个测试数据分类，这比 k-NN 中将测试图像和所有训练数据做比较的方法快多了

理解线性分类器

线性分类器计算图像中 3 个颜色通道中所有像素的值与权重的矩阵乘，从而得到分类分值。根据我们对权重设置的值，对于图像中的某些位置的某些颜色，函数表现出喜好或者厌恶（根据每个权重的符号而定）

举个例子，可以想象船分类就是被大量的蓝色所包围（对应的就是水）。那么船分类器在蓝色通道上的权重就有很多的正权重（它们的出现提高了船分类的分值），而在绿色和红色通道上的权重为负的就比较多（它们的出现降低了船分类的分值）

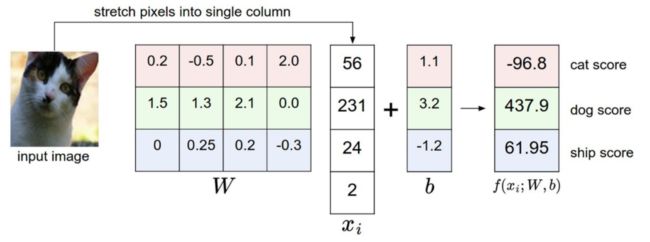
考虑上面的例子，为了便于可视化，假设图像只有 4 个像素（都是黑白像素，这里不考虑 RGB 通道），有 3 个分类（红色代表猫，绿色代表狗，蓝色代表船，注意，这里的红、绿和蓝 3 种颜色仅代表分类，和 RGB 通道没有关系）。首先将图像像素拉伸为一个列向量，与 $W$ 进行矩阵乘，然后得到各个分类的分值。需要注意的是，这个 $W$ 一点也不好：猫分类的分值非常低。从上图来看，算法倒是觉得这个图像是一只狗

将图像看做高维度的点： 既然图像被伸展成为了一个高维度的列向量，那么我们可以把图像看做这个高维度空间中的一个点（即每张图像是 3072 维空间中的一个点）。整个数据集就是一个点的集合，每个点都带有 1 个分类标签

既然定义每个分类类别的分值是权重和图像的矩阵乘，那么每个分类类别的分数就是这个空间中的一个线性函数的函数值。我们没办法可视化 3072 维空间中的线性函数，但假设把这些维度挤压到二维，那么就可以看看这些分类器在做什么了：

在上面的示意图中，每个图像是一个点，有3个分类器。以红色的汽车分类器为例，红线表示空间中汽车分类分数为 0 的点的集合，红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正，且线性升高。红线左边的点分值为负，且线性降低

从上面可以看到， $W$ 的每一行都是一个分类类别的分类器。对于这些数字的几何解释是：如果改变其中一行的数字，会看见分类器在空间中对应的直线开始向着不同方向旋转。而偏差 $b$ ，则允许分类器对应的直线平移。需要注意的是，如果没有偏差，无论权重如何，在 $x_i=0$ 时分类分值始终为 0，这样所有分类器的线都不得不穿过原点

将线性分类器看作模板匹配

关于权重 $W$ 的另一个解释是它的每一行对应着一个分类的模板（有时候也叫作原型）。一张图像对应不同分类的得分，是通过使用内积（也叫点积）来比较图像和模板，然后找到和哪个模板最相似

从这个角度来看，线性分类器就是在利用学习到的模板，针对图像做模板匹配。从另一个角度来看，可以认为还是在高效地使用 k-NN，不同的是我们没有使用所有的训练集的图像来比较，而是每个类别只用了一张图片（这张图片是我们学习到的，而不是训练集中的某一张），而且我们会使用（负）内积来计算向量间的距离，而不是使用L1或者L2距离

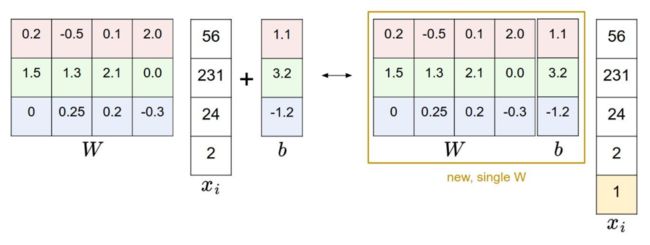
偏差和权重的合并技巧

在进一步学习前，要提一下这个经常使用的技巧。它能够将我们常用的参数 $W$ 和 $b$ 合二为一。回忆一下，分类评分函数定义为： $f(x_i, W, b) = Wx_i+b$

分开处理这两个参数显得有点笨拙，一般常用的方法是把两个参数放到同一个矩阵中，同时 $x_i$ 向量就要增加一个维度，这个维度的数值是常量 1，这就是默认的偏差维度。这样新的公式就简化成下面这样： $f(x_i,W) = Wx_i$

还是以 CIFAR-10 为例，那么 $x_i$ 的大小就变成 $[3073\times1]$ ，而不是 $[3072\times1]$ 了，多出了包含常量 1 的 1 个维度。而 $W$ 大小就是 $[10\times3073]$ 了。 $W$ 中多出来的这一列对应的就是偏差值 $b$ ，具体见下图：

图像数据预处理

在上面的例子中，所有图像都是使用的原始像素值（从 0 到 255）。在机器学习中，对于输入的特征做 『归一化（normalization）』 处理是常见的套路。而在图像分类的例子中，图像上的每个像素可以看做一个特征。在实践中，对每个特征减去平均值来中心化数据是非常重要的。在这些图片的例子中，该步骤意味着根据训练集中所有的图像计算出一个平均图像值，然后每个图像都减去这个平均值，这样图像的像素值就大约分布在 [-127, 127] 之间了。下一个常见步骤是，让所有数值分布的区间变为 [-1, 1]，零均值的中心化是很重要的，等我们理解了梯度下降后再来详细解释

损失函数 Loss Funtion

我们使用损失函数来量化我们对结果的不满意程度，直观的讲，当评分函数输出结果与真实结果之间差异越大，损失函数输出越大，反之越小

多类支持向量机损失 Multiclass Support Vector Machine Loss

损失函数的具体形式多种多样。首先介绍常用的多类支持向量机（SVM）损失函数

SVM 的损失函数想要 SVM 在正确分类上的得分始终比不正确分类上的得分高出一个边界值 $\Delta$ 。如下图，如果其他分类分数进入了红色大的区域，甚至更高，那么就开始计算损失；如果没有这些情况，损失值为 0。我们的目标就是找到一些权重，它们既能够让训练集中的数据样例满足这些限制，也能让总的损失值尽可能地低

让我们更精确一些，评分函数输入像素数据，然后通过公式 $f(x_i,W)$ 计算不同分类类别的分值，我们将这个分值记为 $s$ ，比如针对第 $j$ 个类别的得分就是第 $j$ 个元素 $s_j=f(x_i,W)_j$

针对第 $i$ 个数据的多类 SVM 的损失函数定义为： $L_i=\sum_{j\neq y_i}max(0,s_j-s_{y_i}+\Delta)$

我们举个例子说明这个公式，假设有 3 个分类，并且得到了分值 $s = [13, - 7, 11]$ 。其中第一个类别是正确类别，即 $y_i=0$ 。同时假设 $\Delta$ 是 10（后面会详细介绍该超参数）。上面的公式是将所有不正确分类（ $j\neq y_i$ ）加起来，所以我们得到两个部分： $L_i=max(0, -7-13+10)+max(0,11-13+10)$

可以看到第一个部分结果是 0，这是因为 [-7-13+10] 得到的是负数，经过 $m a x (0, -)$ 函数处理后得到 0，即这一对类别分数和标签的损失值是 0，这是因为正确分类的得分13 与错误分类的得分 -7 的差为 20，高于边界值 10。而 SVM 只关心差距至少要大于 10，更大的差值还是算作损失值为 0

第二个部分计算 [11-13+10] 得到 8。虽然正确分类的得分比不正确分类的得分要高（13 > 11），但是比 10 的边界值还是小了，分差只有 2，这就是为什么损失值等于 8

简而言之，SVM 的损失函数想要正确分类类别 $y_i$ 的分数比不正确类别分数高，而且至少要高 $\Delta$ ，如果不满足这点，就开始计算损失值

那么在这次的模型中，我们面对的是线性评分函数 $f(x_i,W)=Wx_i$ ，所以损失函数可以写为如下的形式 $L_i=\sum_{j\neq y_i}max(0, w^T_jx_i-w^T_{y_i}x_i+\Delta)$

其中， $w_j$ 是权重 $W$ 的第 $j$ 行

最后，我们提一个内容： $m a x (0, -)$ 函数，它常被称为折叶损失。有时候会听到人们使用平方折叶损失 SVM（即 L2-SVM），它使用的是 $max(0,-)^2$ ，将更强烈（平方地而不是线性地）地惩罚过界的边界值

正则化 Regularization

上面损失函数有一个问题。假设有一个数据集和一个权重集 $W$ 能够正确地分类每个数据（即所有的边界都满足，对于所有的 $i$ 都有 $L_i=0$ ）。问题在于这个 $W$ 并不唯一：可能有很多相似的 $W$ 都能正确地分类所有的数据

一个简单的例子：如果 $W$ 能够正确分类所有数据，即对于每个数据，损失值都是 0。那么当 $\lambda > 1$ 时，任何数乘 $\lambda W$ 都能使得损失值为 0，因为这个变化将所有分值的大小都均等地扩大了，所以它们之间的绝对差值也扩大了。举个例子，如果一个正确分类的分值和它最近的错误分类的分值的差距是 15，对 $W$ 乘以 2 将使得差距变成 30

于是，我们希望能向某些特定的权重 $W$ 添加一些偏好，对其他权重则不添加，以此来消除这样的模糊性。这一点是能够实现的，方法是向损失函数增加一个 『正则化惩罚（regularization penalty）』 $R (W)$ 。最常用的正则化惩罚是 L2 范式，L2 范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重： $R(W)=\sum_k\sum_lW_{k,l}^2$

上面的表达式中，将 $W$ 中所有元素平方后求和。注意正则化函数不是数据的函数，它仅基于权重。包含正则化惩罚后，就能够给出完整的多类 SVM 损失函数了，它由两个部分组成：数据损失（data loss），即所有样例的的平均损失 $L_i$ ，以及正则化损失（regularization loss），完整公式如下所示： $L=\underset{data\ loss}{\underbrace{\frac{1}{N}\sum_iL_i}} + \underset{regularization\ loss}{\underbrace{\lambda R(W)}}$ 又， $L=\frac{1}{N}\sum_i\sum_{j\neq y_i}[max(0, f(x_i;W)_j)-f(x_i;W)_{y_i}+\Delta]+\lambda\sum_k\sum_lW_{k,l}^2$

其中， $N$ 是训练集的数据量。现在正则化惩罚添加到了损失函数里面，并用超参数 $\lambda$ 来计算其权重。该超参数无法简单确定，需要通过交叉验证来获取

除了上述理由外，引入正则化惩罚还带来很多良好的性质，比如引入了 L2 惩罚后，SVM 就有了最大边界（max margin）这一良好性质

其中最好的性质就是对大数值权重进行惩罚，可以提升其泛化能力，因为这就意味着没有哪个维度能够独自对于整体分值有过大的影响

举个例子，假设输入向量 $x = [1, 1, 1, 1]$ ，两个权重向量 $w_1=[1, 0, 0, 0]$ ， $w_2=[0.25, 0.25, 0.25, 0.25]$ 。那么 $w_1^Tx=w_2^Tx=1$ ，两个权重向量都得到同样的内积，但是 $w_1$ 的 L2 惩罚是 1.0，而 $w_2$ 的 L2 惩罚是 0.25。因此，根据 L2 惩罚来看，更好，因为它的正则化损失更小。从直观上来看，这是因为 $w_2$ 的权重值更小且更分散。既然 L2 惩罚倾向于更小更分散的权重向量，这就会鼓励分类器最终将所有维度上的特征都用起来，而不是强烈依赖其中少数几个维度。 在后面的课程中可以看到，这一效果将会提升分类器的泛化能力，并避免过拟合

需要注意的是，和权重不同，偏差没有这样的效果，因为它们并不控制输入维度上的影响强度。因此，通常只对权重 $W$ 正则化，而不正则化偏差 $b$ 。在实际操作中，可发现这一操作的影响可忽略不计。最后，因为正则化惩罚的存在，不可能在所有的例子中得到0的损失值，这是因为只有当 $W$ 的特殊情况下，才能得到损失值为 0

实际操作

设置 Delta： 你可能注意到上面的内容对超参数 $\Delta$ 及其设置是一笔带过，那么它应该被设置成什么值？需要通过交叉验证来求得吗？现在看来，该超参数在绝大多数情况下设为 $\Delta=1.0$ 都是安全的。超参数 $\Delta$ 和 $\lambda$ 看起来是两个不同的超参数，但实际上他们一起控制同一个权衡：即损失函数中的数据损失和正则化损失之间的权衡。 理解这一点的关键是要知道，权重 $W$ 的大小对于分类分值有直接影响（当然对他们的差异也有直接影响）：当我们将 $W$ 中的值缩小时，分类分值之间的差异也变小，反之亦然。因此，不同分类分值之间的边界的具体值（比如 $\Delta = 1$ 或 $\Delta=100$ ）从某些角度来看是没意义的，因为权重自己就可以控制差异变大和缩小。也就是说，真正的权衡是我们允许权重能够变大到何种程度（通过正则化强度 $\lambda$ 来控制）

与二元支持向量机（Binary Support Vector Machine）的关系： 二院支持向量机对于第 $i$ 个数据的损失计算公式是： $L_i=Cmax(0,1-y_iw^Tx_i)+R(W)$
其中， $C$ 是一个超参数，并且 $y_i\in\left \{ -1,1 \right \}$ 。可以认为本章节介绍的 SVM 公式包含了上述公式，上述公式是多类支持向量机公式只有两个分类类别的特例。也就是说，如果我们要分类的类别只有两个，那么公式就化为二元 SVM 公式。这个公式中的 $C$ 和多类 SVM 公式中的 $\lambda$ 都控制着同样的权衡，而且它们之间的关系是 $C\propto \frac{1}{\lambda}$

Softmax 分类器

对于学过二元逻辑回归分类器的读者来说，Softmax 分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。在 Softmax 分类器中，映射函数 $f(x_i;W)=Wx_i$ 保持不变，但将这些评分值视为每个分类的为归一化的对数概率，并且将折叶损失替换为交叉熵损失 $L_i=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}})\ or\ L_i=-f_{y_i}+log(\sum_je^{f_j})$
其中，使用 $f_j$ 来表示分类评分向量 $f$ 中的第 $j$ 个元素

和之前一样，整个数据集的损失值是数据集中所有样本数据的损失值 $L_i$ 的均值与正则化损失 $R (W)$ 之和

我们称 $f_j(z)=e^{z_j} / \sum_ke^{z_k}$ 为 Softmax 函数：其输入值是一个向量，向量中元素为任意实数的评分值，函数对其进行压缩，输出一个向量，其中每个元素值在 0 到 1 之间，且所有元素之和为1

从信息论视角， 在真实分布 $p$ 和估计分布 $q$ 之间的交叉熵定义如下： $H(p,q)=-\sum_xp(x)logq(x)$

因此，Softmax 分类器所做的就是最小化在估计分类概率和真实分布之间的交叉熵，所谓真实分布就是所有概率密度都分布在正确的类别上

既然交叉熵可以写成熵和相对熵的形式： $H(p,q)=H(p)+D_{KL}(p||q)$ ，并且 Delta 函数 $p$ 的熵是 0，那么就能等价的看作是对两个分布之间的相对熵做最小化操作

换句话说，交叉熵损失函数想要预测分布的所有概率密度都在正确分类上

从概率论角度， 我们先理解下面这个公式 $P(y_i|x_i,W)=\frac{e^{f_{y_i}}}{\sum_je^{f_j}}$ 可以解释为给定图像数据 $x_i$ ，以 $W$ 为参数，分配给正确分类标签 $y_i$ 的归一化概率

那么我们在最小化正确分类的负对数概率，就可以看作是在进行最大似然估计。该解释的另一个好处是，损失函数中的正则化部分 $R (w)$ 可以被看作是权重矩阵 $W$ 的高斯先验，这里进行的就是最大后验估计而不是最大似然估计

编程实现 Softmax 函数计算的时候，中间项 $e^{f_{y_i}}$ 和 $\sum_je^{f_j}$ 因为存在子树函数，所以数字可能非常大。除以大数字可能导致数值计算的不稳定，所以学会使用归一化技巧十分重要

如果在分式的分子和分母都成一个常数 $C$ ，并把它变换到求和中，就能得到一个从数学上等价的公式 $\frac{e^{f_{y_i}}}{\sum_je^{f_j}}=\frac{Ce^{f_{y_i}}}{C\sum_je^{f_j}}=\frac{e^{f_{y_i}+logC}}{\sum_je^{f_j+logC}}$

$C$ 的值可以自由选择，不会影响计算结果，通过使用这个技巧可以提高计算中的数值稳定性，通常将 $C$ 设为 $logC=-max_jf_j$

该技巧简单地说，就是将向量 $f$ 中的数字进行平移，使得最大值为 0

SVM 和 Softmax 的比较

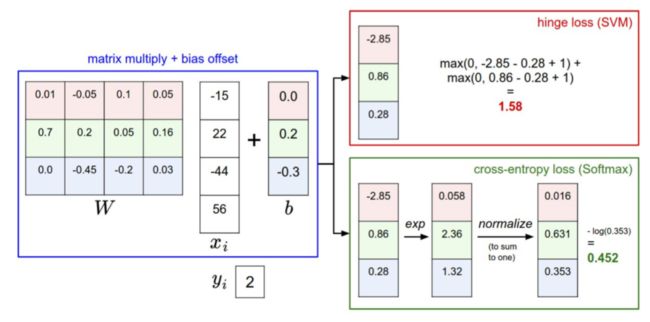
两个分类器都计算了同样的分值向量 $f$ 。不同之处在于对 $f$ 中分值的解释：SVM 分类器将它们看做是分类评分，它的损失函数鼓励正确的分类（本例中是蓝色的类别 2）的分值比其他分类的分值高出至少一个边界值。Softmax 分类器将这些数值看做是每个分类没有归一化的对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。SVM 的最终的损失值是 1.58，Softmax 的最终的损失值是 0.452，但要注意这两个数值没有可比性。只在给定同样数据，在同样的分类器的损失值计算中，它们才有意义

Softmax 分类器为每个分类提供了可能性：SVM 的计算是无标定的，而且难以针对所有分类的评分值给出直观解释。Softmax 分类器则不同，它允许我们计算出对于所有分类标签的可能性

我们解释一下这里所谓的可能性，这个可能性分布的集中或离散程度是由正则化参数 $\lambda$ 直接决定的， $\lambda$ 是你能直接控制的一个输入参数。举个例子，假设 3 个分类的原始分数是 $[1, - 2, 0]$ ，那么 softmax 函数就会计算： $[1,-2,0]\rightarrow[e^1,e^{-2},e^0]=[2.71,0.14,1]\rightarrow[0.7,0.04,0.26]$

现在，如果正则化参数 $\lambda$ 更大，那么权重 $W$ 就会被惩罚的更多，然后它的权重数值就会更小。这样算出来的分数也会更小，假设小了一半吧，即 $[0.5, - 1, 0]$ ，那么softmax 函数的计算就是： $[0.5,-1,0]\rightarrow[e^{0.5},e^{-1},e^0]=[1.65,0.73,1]\rightarrow[0.55,0.12,0.33]$

现在看起来，概率的分布就更加分散了。还有，随着正则化参数 $\lambda$ 不断增强，权重数值会越来越小，最后输出的概率会接近于均匀分布。这就是说，softmax 分类器算出来的概率最好是看成一种对于分类正确性的自信。和 SVM 一样，数字间相互比较得出的大小顺序是可以解释的，但其绝对值则难以直观解释

在实际使用中，SVM 和 Softmax 经常是相似的：虑一个评分是 [10, -2, 3] 的数据，其中第一个分类是正确的。那么一个SVM（ $\Delta=1$ ）会看到正确分类相较于不正确分类，已经得到了比边界值还要高的分数，它就会认为损失值是 0。SVM对于数字个体的细节是不关心的：如果分数是 [10, -100, -100] 或者 [10, 9, 9]，对于SVM来说没设么不同，只要满足超过边界值等于 1，那么损失值就等于 0

对于 Softmax 分类器，情况则不同。对于 [10, 9, 9] 来说，计算出的损失值就远远高于 [10, -100, -100] 。换句话来说，Softmax 分类器对于分数是永远不会满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小

但是，SVM 只要边界值被满足了就满意了，不会超过限制去细微地操作具体分数。这可以被看做是 SVM 的一种特性。举例说来，一个汽车的分类器应该把它的大量精力放在如何分辨小轿车和大卡车上，而不应该纠结于如何与青蛙进行区分，因为区分青蛙得到的评分已经足够低了

损失函数可视化

我们可以通过数学公式来解释损失函数的分段线性结构，对于一个单独的数据，有损失函数的计算公式如下 $L_i=\sum_{j\neq y_i}[max(0,w^T_jx_i-w^T_{y_i}+1)]$

通过公式可见，每个样本的数据损失值是以 $W$ 为参数的线性函数的总和。 $W$ 的每一行（即 $w_j$ ），有时候它前面是一个正好（比如当它对应错误分类的时候），有时候它前面是一个负号（比如当它是正确分类的时候）

假设有一个简单的数据集，其中包含有 3 个只有 1 个维度的点，数据集数据点有 3 个类别。那么完整的无正则化SVM的损失值计算如下：

$L_0=max(0,w^T_1x_0-w^T_0x_0+1)+max(0,w^T_2x_0-w^T_0x_0+1) \\ L_1=max(0,w^T_0x_1-w^T_1x_1+1)+max(0,w^T_2x_1-w^T_1x_1+1) \\ L_2=max(0,w^T_0x_2-w^T_2x_2+1)+max(0,w^T_1x_2-w^T_2x_2+1) \\ L = (L_0+L_1+L_2)/3$

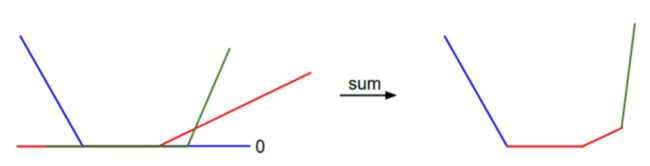
因为这些例子都是一维的，所以数据 $x_i$ 和权重 $w_j$ 都是数字。观察 $w_0$ ，可以看到上面的式子中一些项是 $w_0$ 的线性函数，且每一项都会与 0 比较，取两者的最大值。可作出如上的图，x 轴方向就是一个权重，y 轴就是损失值。数据损失是多个部分组合而成。其中每个部分要么是某个权重的独立部分，要么是该权重的线性函数与 0 阈值的比较。完整的SVM数据损失就是这个形状的 30730 维版本

由于 max 操作，损失函数中存在一些 『不可导点（kinks）』，这些点使得损失函数不可微，因为在这些不可导点，梯度是没有定义的。但是 『次梯度（subgradient）』 依然存在且常常被使用

最优化

损失函数可以量化某个具体权重集 $W$ 的质量。而最优化的目标就是找到能够最小化损失函数值的 $W$

我们现在就朝着这个目标前进，实现一个能够最优化损失函数的方法。对于有一些经验的同学，这节课看起来有点奇怪，因为使用的例子（SVM 损失函数）是一个凸函数问题。但是要记得，最终的目标是不仅仅对凸函数做最优化，而是能够最优化一个神经网络，而对于神经网络是不能简单的使用凸函数的最优化技巧的

梯度计算：有两种方法，个是缓慢的近似方法（数值梯度法），但实现相对简单。另一个方法（分析梯度法）计算迅速，结果精确，但是实现时容易出错，且需要使用微分

数值梯度法

对一维函数的求导公式如下 $\frac{df(x)}{dx}=\underset{h\rightarrow0}{lim}\frac{f(x+h)-f(x)}{h}$

下面代码是一个输入为函数 $f$ 和向量 $x$ ，计算 $f$ 的梯度的通用函数，它返回函数在点 $x$ 处的梯度

def eval_numerical_gradient(f, x):
  """  
  一个f在x处的数值梯度法的简单实现
  - f是只有一个参数的函数
  - x是计算梯度的点
  """ 

  fx = f(x) # 在原点计算函数值
  grad = np.zeros(x.shape)
  h = 0.00001

  # 对x中所有的索引进行迭代
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # 计算x+h处的函数值
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # 增加h
    fxh = f(x) # 计算f(x + h)
    x[ix] = old_value # 存到前一个值中 (非常重要)

    # 计算偏导数
    grad[ix] = (fxh - fx) / h # 坡度
    it.iternext() # 到下个维度

  return grad

根据上面的梯度公式，代码对所有维度进行迭代，在每个维度上产生一个很小的变化 $h$ ，通过观察函数值变化，计算函数在该维度上的偏导数。最后，所有的梯度存储在变量 $g r a d$ 中

注意在数学公式中， $h$ 的取值是趋近于 0 ，然而在实际中，用一个很小的数值（比如例子中的1e-5）就足够了。在不产生数值计算出错的理想前提下，你会使用尽可能小的 $h$ ，还有，实际中用中心差值公式（centered difference formula） $[f (x + h) - f (x - h)] / 2$ 效果较好

步长的影响：梯度指明了函数在哪个方向是变化率最大的，但是没有指明在这个方向上应该走多远。在后续的课程中可以看到，选择步长（也叫作学习率）将会是神经网络训练中最重要（也是最头痛）的超参数设定之一。还是用蒙眼徒步者下山的比喻，这就好比我们可以感觉到脚朝向的不同方向上，地形的倾斜程度不同。但是该跨出多长的步长呢？不确定。如果谨慎地小步走，情况可能比较稳定但是进展较慢（这就是步长较小的情况）。相反，如果想尽快下山，那就大步走吧，但结果也不一定尽如人意。有时就会出现反例，在某些点如果步长过大，反而可能越过最低点导致更高的损失值

微分分析计算梯度

数值梯度法使用有限差值近似计算梯度，实现比较简单，但缺点在于终究只是近似，且计算花费太大。利用微分来分析，能得到计算梯度的公式，而不是近似，用公式计算梯度速度更快，但是唯一的不好就是实现时容易出错。为了解决这个问题，在实际操作中常常将分析梯度法的结果和数值梯度法的结果作比较，以检查其实现的正确性，这步叫做 『梯度检查』
用SVM的损失函数在某个数据点上的计算来举例 $L_i=\sum_{j\neq y_i}[max(0,w^T_jx_i-w^T_{y_i}+\Delta)]$

对 $w_{y_i}$ 进行微分得到 $\bigtriangledown _{w_{y_i}}L_i=-(\sum_{i\neq y_i}1(w^T_jx_i-w^T_{y_i}+\Delta>0))x_i$

上面公式中 $1$ 是一个示性函数，如果括号中的条件为真，那么函数值为 1，如果为假，则函数值为 0

虽然上述公式看起来复杂，但在代码实现的时候比较简单：只需要计算没有满足边界值的分类的数量（因此对损失函数产生了贡献），然后乘以 $x_i$ 就是梯度了。注意，这个梯度只是对应正确分类的 $W$ 的行向量的梯度，那些 $j\neq y_i$ 行的梯度是： $\bigtriangledown _{w_{y_i}}L_i=1(w^T_jx_i-w^T_{y_i}+\Delta>0)x_i$

一旦将梯度的公式微分出来，代码实现公式并用于梯度更新就比较顺畅了

梯度下降

现在可以计算损失函数的梯度了，程序重复地计算梯度然后对参数进行更新，这一过程称为梯度下降，它的普通版本是这样的：

# 普通的梯度下降

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # 进行梯度更新

这个简单的循环在所有的神经网络核心库中都有

小批量数据梯度下降

对于量级非常大的训练数据，一步步训练整个数据集是不现实的。因此，有一个常用的方法就是计算训练集中的小批量数据。例如，

# 普通的小批量数据梯度下降

while True:
  data_batch = sample_training_data(data, 256) # 256个数据
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # 参数更新

这个方法之所以效果不错，是因为训练集中的数据都是相关的。要理解这一点，可以想象一个极端情况：在 ILSVRC 中的 120 万个图像是 1000 张不同图片的复制（每个类别 1 张图片，每张图片有 1200 张复制）。那么显然计算这 1200 张复制图像的梯度就应该是一样的。对比 120 万张图片的数据损失的均值与只计算 1000 张的子集的数据损失均值时，结果应该是一样的。实际情况中，数据集肯定不会包含重复图像，那么小批量数据的梯度就是对整个数据集梯度的一个近似。因此，在实践中通过计算小批量数据的梯度可以实现更快速地收敛，并以此来进行更频繁的参数更新

小批量数据策略有个极端情况，那就是每个批量中只有 1 个数据样本，这种策略被称为 『随机梯度下降』（Stochastic Gradient Descent，简称 SGD）

小批量数据的大小是一个超参数，但是一般并不需要通过交叉验证来调参。它一般由存储器的限制来决定的，或者干脆设置为同样大小，比如 32，64，128 等。之所以使用 2 的指数，是因为在实际中许多向量化操作实现的时候，如果输入数据量是 2 的倍数，那么运算更快

反向传播的直观理解

反向传播是一个优美的局部过程。在整个计算线路图中，每个门单元都会得到一些输入并立即计算两个东西：

这个门的输出值
其输出值关于输入值的局部梯度

门单元完成这两件事是完全独立的，它不需要知道计算线路中的其他细节。然而，一旦前向传播完毕，在反向传播的过程中，门单元门将最终获得整个网络的最终输出值在自己的输出值上的梯度。链式法则指出，门单元应该将回传的梯度乘以它对其的输入的局部梯度，从而得到整个网络的输出对该门单元的每个输入值的梯度

模块化：Sigmoid 例子

我们看一个表达式： $f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}}$ 这个表达式描述了一个含输入 $x$ 和权重 $w$ 的 2 维神经元，该神经元使用 sigmoid 激活函数。这个函数由多个门组成：

$f(x)=\frac{1}{x}\rightarrow \frac{df}{dx}=-\frac{1}{x^2} \\ f_c(x)=c+x\rightarrow \frac{df}{dx}=1,\ f(x) = e^x\rightarrow \frac{df}{dx}=e^x \\ f_a(x)=ax\rightarrow \frac{df}{dx}=a$

其中， $f_c$ 对输入值进行了常量 $c$ 的平移， $f_a$ 将输入值扩大了常量 $a$ 倍。整个计算路线如下：

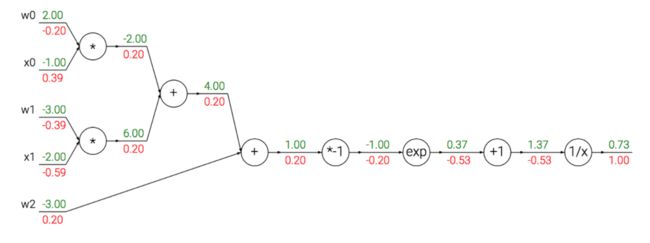
在上面的例子中可以看见一个函数操作的长链条，链条上的门都对 $w$ 和 $x$ 的点积结果进行操作。该函数被称为 sigmoid 函数 $\sigma(x)$

sigmoid 函数关于其输入的求导是可以简化的（使用了在分子上先加后减 1 的技巧）：

$\sigma(x)=\frac{1}{1+e^{-x}}\rightarrow$
$\frac{d\sigma(x)}{dx}=\frac{e^{-x}}{(1+e^{-x})^2}=\left ( \frac{1+e^{-x}-1}{1+e^{-x}} \right )\left ( \frac{1}{1+e^{-x}} \right )=(1-\sigma(x))(\sigma(x))$

由此一来，梯度计算简单了许多。举个例子，sigmoid 表达式输入为 1.0，则在前向传播中计算出输出为 0.73。根据上面的公式，局部梯度为 (1 - 0.73) * 0.73 ≈ 0.2，和之前的计算流程比起来，现在的计算使用一个单独的简单表达式即可。因此，在实际的应用中将这些操作装进一个单独的门单元中将会非常有用

对前向传播变量进行缓存：在计算反向传播时，前向传播过程中得到的一些中间变量非常有用。在实际操作中，最好代码实现对于这些中间变量的缓存，这样在反向传播的时候也能用上它们

在不同分支的梯度要相加：如果变量 $x, y$ 在前向传播的表达式中出现多次，那么进行反向传播的时候就要非常小心，使用 += 而不是 = 来累计这些变量的梯度（不然就会造成覆盖）。这是遵循了在微积分中的多元链式法则，该法则指出如果变量在线路中分支走向不同的部分，那么梯度在回传的时候，就应该进行累加

回传流中的模式

一个有趣的现象是在多数情况下，反向传播中的梯度可以被很直观地解释。例如神经网络中最常用的加法、乘法和取最大值这三个门单元，它们在反向传播过程中的行为都有非常简单的解释。先看下面这个例子：

加法门单元：把输出的梯度相等地分发给它所有的输入，这一行为与输入值在前向传播时的值无关。这是因为加法操作的局部梯度都是简单的 +1，所以所有输入的梯度实际上就等于输出的梯度，因为乘以 1.0 保持不变。上例中，加法门把梯度 2.00 不变且相等地路由给了两个输入

取最大值门单元：对梯度做路由——和加法门不同，取最大值门将梯度转给其中一个输入，这个输入是在前向传播中值最大的那个输入。这是因为在取最大值门中，最高值的局部梯度是 1.0，其余的是 0。上例中，取最大值门将梯度 2.00 转给了 $z$ 变量，因为 $z$ 的值比 $w$ 高，于是 $w$ 的梯度保持为0。

乘法门单元：相对不容易解释。它的局部梯度就是输入值，但是是相互交换之后的，然后根据链式法则乘以输出值的梯度。上例中， $x$ 的梯度是 -4.00 × 2.00 = -8.00

注意一种比较特殊的情况，如果乘法门单元的其中一个输入非常小，而另一个输入非常大，那么乘法门的操作将会不是那么直观：它将会把大的梯度分配给小的输入，把小的梯度分配给大的输入。在线性分类器中，权重和输入是进行点积 $w^Tx_i$ ，这说明输入数据的大小对于权重梯度的大小有影响。例如，在计算过程中对所有输入数据样本 $x_i$ 乘以 $1000$ ，那么权重的梯度将会增大 $1000$ 倍，这样就必须降低学习率来弥补。这就是为什么数据预处理关系重大，它即使只是有微小变化，也会产生巨大影响。对于梯度在计算线路中是如何流动的有一个直观的理解，可以帮助读者调试网络

作为线性分类器的单个神经元

神经元模型的前向计算数学公式看起来可能比较眼熟。就像在线性分类器中看到的那样，神经元有能力 “ 喜欢 ”（激活函数值接近 1），或者 “ 不喜欢 ”（激活函数值接近 0）输入空间中的某些线性区域。因此，只要在神经元的输出端有一个合适的损失函数，就能让单个神经元变成一个线性分类器

二分类 Softmax 分类器

我们可以把 $\sigma(\sum_iw_ix_i+b)$ 看作其中一个分类的概率 $P(y_i=1|x_i;w)$ ，其他分类的概率为 $P(y_i=0|x_i,w)=1-P(y_i=1|x_i;w)$ 。根据这种理解，可以得到交叉熵损失，然后将它最优化为二分类的 Softmax 分类器。因为 sigmoid 函数输出限定在 0 - 1 之间，所以分类器作预测的基准是神经元的输出是否大于 0.5、

二分类 SVM 分类器

或者可以在神经元的输出外增加一个最大边界折叶损失函数，将其训练为一个二分类为的支持向量机

理解正则化

正则损失从生物学的角度可以看做逐渐遗忘，因为它的效果就是让所有突触的权重 $w$ 在参数更新的过程中逐渐向 0 变化

常用激活函数

Sigmoid

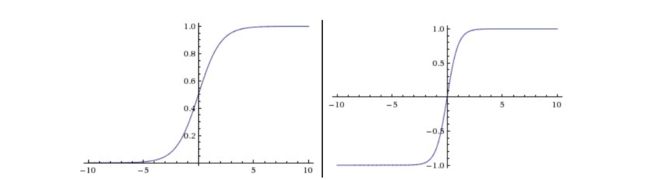
sigmoid 非线性函数的数学公式是 $\sigma(x)=\frac{1}{1+e^{-x}}$ ，函数图像如下图的左边所示。在前面已经提到过，它输入实数值并将其挤压到 0 到 1 范围内。更具体地说，很大的负数变成 0，很大的正数变成 1

在历史上，sigmoid 函数非常常用，这是因为它对于神经元的激活频率有良好的解释：从完全不激活（0）到在求和后的最大频率处的完全饱和的激活（1）。然而现在 sigmoid 函数已经不太受欢迎，实际很少使用了，这是因为它有两个主要缺点：

sigmoid 函数饱和使梯度消失
sigmoid 神经元有一个不好的特性，就是当神经元的激活在接近 0 或 1 处时会饱和：在这些区域，梯度几乎为 0。回忆一下，在反向传播的时候，局部梯度将会与整个损失函数关于该门单元输出的梯度相乘。因此，如果局部梯度非常小，那么相乘的结果也会接近零，这会出现杀死梯度的情况，几乎没有信号通过神经元传到权重再到数据了。还有，为了防止饱和，必须对于权重矩阵初始化特别留意。比如，如果初始化权重过大，那么大多数神经元将会饱和，导致网络就几乎不学习了
sigmoid 函数的输出不是零中心的
这个性质并不是我们想要的，sigmoid 函数导致在神经网络后面层中的神经元得到的数据不是零中心的。这一情况将影响梯度下降的运作，因为如果输入神经元的数据总是正数（比如在 $f=w^tx+b$ 中每个元素都 $x > 0$ ），那么关于 $w$ 的梯度在反向传播的过程中，将会要么全部是正数，要么全部是负数（具体依整个表达式 $f$ 而定）。这将会导致梯度下降权重更新时出现 Z 字型的下降。然而，可以看到整个批量数据的梯度被加起来后，对于权重的最终更新将会有不同的正负，这样就从一定程度上减轻了这个问题。因此，该问题相对于上面的神经元饱和问题来说只是个小麻烦，没有那么严重

Tanh

tanh 非线性函数图像如上图右边所示。它将实数值压缩到 [-1,1] 之间。和 sigmoid 神经元一样，它也存在饱和问题，但是和 sigmoid 神经元不同的是，它的输出是零中心的。因此，在实际操作中，tanh 非线性函数比 sigmoid 非线性函数更受欢迎。注意 tanh 神经元是一个简单放大的 sigmoid 神经元，具体说来就是： $tanh(x)=2\sigma(2x)-1$

ReLU

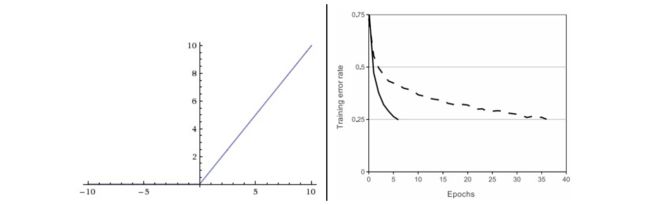
它的函数公式是 $f (x) = m a x (0, x)$ ，换句话说，这个激活函数就是一个关于 0 的阈值。使用ReLU有以下一些优缺点：

相较于 sigmoid 和 tanh 函数，ReLU 对于随机梯度下降的收敛有巨大的加速作用（ Krizhevsky 等的论文指出有 6 倍之多）。据称这是由它的线性，非饱和的公式导致的
sigmoid 和 tanh 神经元含有指数运算等耗费计算资源的操作，而 ReLU 可以简单地通过对一个矩阵进行阈值计算得到

但是，ReLu 在使用时也有一定的缺点：

在训练的时候，ReLU单元比较脆弱并且可能死掉
举例来说，当一个很大的梯度流过 ReLU 的神经元的时候，可能会导致梯度更新到一种特别的状态，在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生，那么从此以后流过这个神经元的梯度将都变成 0。也就是说，这个 ReLU 单元在训练中将出现不可逆转的死亡，因此导致了数据多样化的丢失。如果学习率设置得太高，可能会发现网络中 40% 的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。因此，通过合理设置学习率，可以降低这种情况发生的概率

Leaky ReLU

Leaky ReLU 是解决 ReLU 死亡问题的尝试。ReLU 中当 $x < 0$ 时，函数值为 0。而 Leaky ReLU 则是给出一个很小的负数梯度值，比如 0.01。所以其函数公式为 $f(x)=1(x<0)(\alpha x)+1(x\geqslant0)$ ，其中[公式]是一个小的常量。有些研究者的论文指出这个激活函数表现很不错，但是其效果并不是很稳定。Kaiming He 等人在 2015 年发布的论文 Delving Deep into Rectifiers 中介绍了一种新方法 PReLU，把负区间上的斜率当做每个神经元中的一个参数。然而,该激活函数在在不同任务中均有益处的一致性并没有特别清晰

Maxout

Maxout 是对 ReLU 和 leaky ReLU 的一般化归纳，它的函数是： $f(x)=max(w^T_1x+b1,w^T_2x+b2)$ 。ReLU 和 Leaky ReLU 都是这个公式的特殊情况（比如 ReLU 就是当 $w_1,b_1=0$ 的时候）。这样 Maxout 神经元就拥有 ReLU 单元的所有优点（线性操作和不饱和），而没有它的缺点（死亡单元）。然而和 ReLU 对比，它每个神经元的参数数量增加了一倍，其最大的缺点就是导致整体参数的数量激增

神经网络结构

对于普通神经网络，最普通的层的类型就是 『全连接层（fully-connected layer）』，全连接层中的神经元与其前后两层的神经元是完全成对连接的，但是在同一个全连接层内的神经元之间没有连接

命名规则

当我们说 $N$ 层神经网络的时候，我们没有把输入层算入。因此，单层的神经网络就是没有隐层的（输入直接映射到输出）。因此，有的研究者会说逻辑回归或者 SVM 只是单层神经网络的一个特例。研究者们也会使用人工神经网络（Artificial Neural Networks 缩写 ANN）或者多层感知器（Multi-Layer Perceptrons 缩写 MLP）来指代神经网络。很多研究者并不喜欢神经网络算法和人类大脑之间的类比，他们更倾向于用单元（unit）而不是神经元作为术语

输出层

和神经网络中其他层不同，输出层的神经元一般是不会有激活函数的（或者也可以认为它们有一个线性相等的激活函数）。这是因为最后的输出层大多用于表示分类评分值，因此是任意值的实数，或者某种实数值的目标数（比如在回归中）

确定网络尺寸

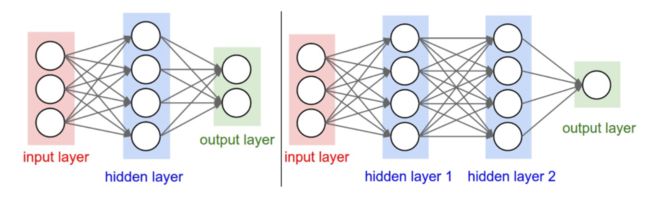
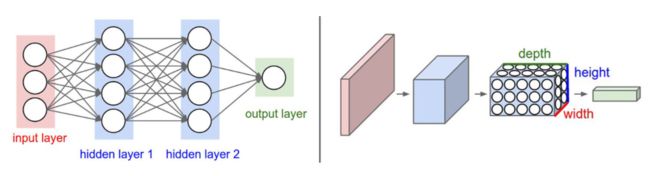
用来度量神经网络的尺寸的标准主要有两个：一个是神经元的个数，另一个是参数的个数，用上面图示的两个网络举例：

第一个网络有 4 + 2 = 6个神经元（输入层不算），[ 3 x 4 ] + [ 4 x 2 ] = 20 个权重，还有 4 + 2 = 6 个偏置，共 26 个可学习的参数
第二个网络有 4 + 4 + 1 = 9 个神经元，[ 3 x 4 ] + [ 4 x 4 ] + [ 4 x 1 ] = 32个权重，4 + 4 + 1 = 9 个偏置，共 41 个可学习的参数。

前向传播计算举例

不断重复的矩阵乘法与激活函数交织。将神经网络组织成层状的一个主要原因，就是这个结构让神经网络算法使用矩阵向量操作变得简单和高效

用上面那个 3 层神经网络举例，输入是 [ 3 x 1 ] 的向量。一个层所有连接的强度可以存在一个单独的矩阵中。比如第一个隐层的权重 $W_1$ 是 [ 4 x 3 ]，所有单元的偏置储存在 $b_1$ 中，尺寸 [ 4 x 1 ]。这样，第一个隐藏层中的每个神经元的权重都在 $W_1$ 的一个行中，于是矩阵乘法np.dot(W1, x) 就能计算该层中所有神经元的激活数据。类似的， $W_2$ 将会是 [ 4 x 4 ] 矩阵，存储着第二个隐层的连接， $W_3$ 是 [ 1 x 4 ] 的矩阵，用于输出层。完整的 3 层神经网络的前向传播就是简单的 3 次矩阵乘法，其中交织着激活函数的应用

# 一个3层神经网络的前向传播:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # 激活函数(用的sigmoid)
x = np.random.randn(3, 1) # 含3个数字的随机输入向量(3x1)
h1 = f(np.dot(W1, x) + b1) # 计算第一个隐层的激活数据(4x1)
h2 = f(np.dot(W2, h1) + b2) # 计算第二个隐层的激活数据(4x1)
out = np.dot(W3, h2) + b3 # 神经元输出(1x1)

在上面的代码中，W1、W2、W3、b1、b2、b3 都是网络中可以学习的参数。注意 x 并不是一个单独的列向量，而可以是一个批量的训练数据（其中每个输入样本将会是 x 中的一列），所有的样本将会被并行化的高效计算出来

全连接层的前向传播一般就是先进行一个矩阵乘法，然后加上偏置并运用激活函数

表达能力

理解具有全连接层的神经网络的一个方式是：可以认为它们定义了一个由一系列函数组成的函数族，网络的权重就是每个函数的参数。如此产生的问题是：该函数族的表达能力如何？存在不能被神经网络表达的函数吗？

现在看来，拥有至少一个隐层的神经网络是一个通用的近似器。有研究证明，给出任意连续函数 $f (x)$ 和任意 $\epsilon>0$ ，均存在一个至少含 1 个隐藏层的神经网络 $g (x)$ （并且网络中有合理选择的非线性激活函数），对于 $\forall x$ ，使得 $|f(x)-g(x)|<\epsilon$

换句话说，神经网络可以近似任何连续函数

既然一个隐层就能近似任何函数，那为什么还要构建更多层来将网络做得更深？答案是：虽然一个 2 层网络在数学理论上能完美地近似所有连续函数，但在实际操作中效果相对较差.在一个维度上，虽然以 $a, b, c$ 为参数向量指示块之和函数 $g(x)=\sum_ic_i1(a_ig(x)=∑ici1(ai<x<bi)$

神经网络在实践中非常好用，是因为它们表达出的函数不仅平滑，而且对于数据的统计特性有很好的拟合。同时，网络通过最优化算法（例如梯度下降）能比较容易地学习到这个函数。类似的，虽然在理论上深层网络（使用了多个隐层）和单层网络的表达能力是一样的，但是就实践经验而言，深度网络效果比单层网络好

另外，在实践中 3 层的神经网络会比 2 层的表现好，然而继续加深（做到 4，5，6层）很少有太大帮助。卷积神经网络的情况却不同，在卷积神经网络中，对于一个良好的识别系统来说，深度是一个极端重要的因素（比如数十个可学习的层）。对于该现象的一种解释观点是：因为图像拥有层次化结构（比如脸是由眼睛等组成，眼睛又是由边缘组成），所以多层处理对于这种数据就有直观意义

设置层的数量和尺寸

我们知道当增加层的数量和尺寸时，网络的容量也就上升了。即神经元们可以合作表达许多复杂函数，所能表达的函数空间增加。例如，如果有一个在二维平面上的二分类问题。我们可以训练 3 个不同的神经网络，每个网络都只有一个隐层，但是每层的神经元数目不同

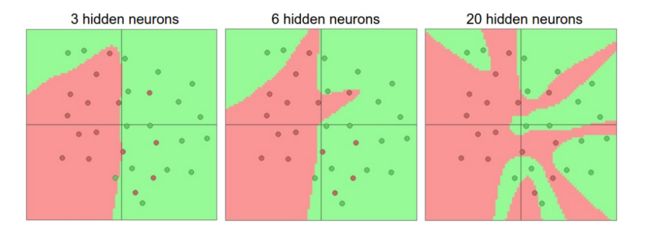
更多神经元的神经网络可以表达更复杂的函数，这既是有时也是不足——优势是可以分类更复杂的数据，不足是可能造成过拟合

『过拟合（Overfitting）』 是网络对数据中的噪声有很强的拟合能力，而没有重视数据间（假设）的潜在基本关系

举例来说，上面有 20 个神经元隐层的网络拟合了所有的训练数据，但是其代价是把决策边界变成了许多不相连的红绿区域。而有 3 个神经元的模型的表达能力只能用比较宽泛的方式去分类数据。它将数据看做是两个大块，并把个别在绿色区域内的红色点看做噪声。在实际中，这样可以在测试数据中获得更好的泛化能力

基于上面的讨论，看起来如果数据不是足够复杂，则似乎小一点的网络更好，因为可以防止过拟合。然而并非如此，防止神经网络的过拟合有很多方法（L2正则化，dropout和输入噪音等），在实践中，使用这些方法来控制过拟合比减少网络神经元数目要好得多

不要减少网络神经元数目的主要原因在于小网络更难使用梯度下降等局部方法来进行训练：虽然小型网络的损失函数的局部极小值更少，也比较容易收敛到这些局部极小值，但是这些最小值一般都很差，损失值很高。相反，大网络拥有更多的局部极小值，但就实际损失值来看，这些局部极小值表现更好，损失更小。因为神经网络是非凸的，就很难从数学上研究这些特性。即便如此，还是有一些文章尝试对这些目标函数进行理解。在实际中，你将发现如果训练的是一个小网络，那么最终的损失值将展现出多变性：某些情况下运气好会收敛到一个好的地方，某些情况下就收敛到一个不好的极值。相反，如果你训练一个大的网络，你将发现许多不同的解决方法，但是最终损失值的差异将会小很多。这就是说，所有的解决办法都差不多，而且对于随机初始化参数好坏的依赖也会小很多

重申一下，正则化强度是控制神经网络过拟合的好方法。看下图结果：

我们对有 20 个隐藏神经元的网络使用不同强度的正则化，可以发现随着正则化强度的增加，网络的决策边界将变得更加平滑

数据预处理

关于数据预处理我们有 3 个常用的符号，数据矩阵 $X$ ，假设其尺寸是 $\times D]$ （ $N$ 是数据样本的数量， $D$ 是数据的维度）

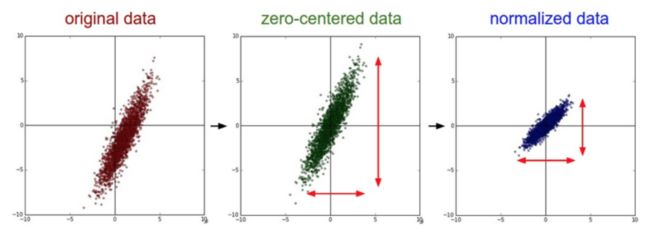
均值减法

它对数据中每个独立特征减去平均值，从几何上可以理解为在每个维度上都将数据云的中心迁移到原点。对于图像，更常用的是对所有像素都减去一个值，可以用 X-=np.mean(X) 实现，也可以在三个颜色通道上分别操作

归一化

归一化是指将数据的所有维度都归一化，使其数字范围都近似相等。有两种常用方法可以实现归一化，

第一种是先对数据做零中心化处理，然后每个维度都除以其标准差，实现代码为 X/=np.std(X,axis=0)
第二种方法是对每个维度都做归一化，使得每个维度的最大和最小值是 1 和 -1。这个预处理操作只有在确信不同的输入特征有不同的数值范围（或计量单位）时才有意义。在图像处理中，由于像素的数值范围几乎是一致的（都在 0 - 255 之间），所以进行这个额外的预处理步骤不是很必要

PCA 和白化

在这种预处理中，相对数据进行零中心化处理，然后计算协方差矩阵，它展示了数据中的相关性结构

# 假设输入数据矩阵X的尺寸为[N x D]
X -= np.mean(X, axis = 0) # 对数据进行零中心化(重要)
cov = np.dot(X.T, X) / X.shape[0] # 得到数据的协方差矩阵

数据协方差矩阵的第 $(i, j)$ 个元素是数据第 $i$ 个和第 $j$ 个维度的协方差。具体来说，该矩阵的对角线上的元素是方差。还有，协方差矩阵是对称和半正定的。我们可以对数据协方差矩阵进行 SVD（奇异值分解）运算

U,S,V = np.linalg.svd(cov)

U 的列是特征向量，S 是装有奇异值的 1 维数组（因为 cov 是对称且半正定的，所以 S 中元素是特征值的平方）。为了去除数据相关性，将已经零中心化处理过的原始数据投影到特征基准上：

Xrot = np.dot(X,U) # 对数据去相关性

注意，U 的列是标准正交向量的集合，所以可以把它们看作标准正交向量。因此，投影对应 X 中的数据的一个旋转，旋转产生的结果就是新的特征向量。如果计算 Xrot 的协方差矩阵，将会看到它是对角对称的。np.linalg.svd 的一个良好性质是在它的返回值 U 中，特征向量是按照特征值的大小排列的。我们可以利用这个性质对数据降维，只要使用前面的小部分特征向量，丢弃掉那些包含的数据没有方差的维度。这个操作也被称为主成分分析降维

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced 变成 [N x 100]

经过上面的操作，将原始的数据集的大小由 [ N x D ] 降到了 [ N x 100 ]，留下了数据中包含最大方差的 100 个维度。通常使用 PCA 降维过的数据训练线性分类器和神经网络会达到非常好的性能效果，同时还能节省时间和存储器空间

最后一个在实践中会看到的变化是白化。白化操作的输入是特征基准上的数据，然后对每个维度除以其特征值来对数值范围进行归一化。该变换的几何解释是：如果数据服从多变量的高斯分布，那么经过白化后，数据的分布将会是一个均值为零，且协方差相等的矩阵

# 对数据进行白化操作:
# 除以特征值 
Xwhite = Xrot / np.sqrt(S + 1e-5)

注意，分母中添加了 1e-5（或者一个更小的常量）来防止分母变为 0。该变换的一个缺陷是在变换的过程中可能会夸大数据中的噪声，这是因为它将所有维度都拉伸到相同的数字范围，这些维度中也包含了那些只有极少差异性（方差小）而大多是噪声的维度。在实际操作中，这个问题可以用更强的平滑来解决，例如采用比 1e-5 更大的值

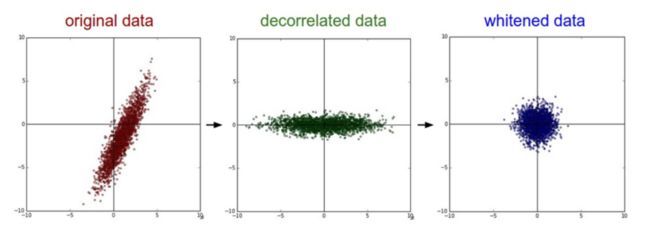
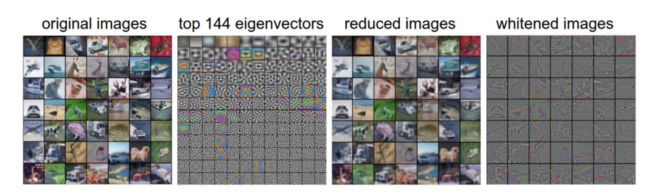
我们对 CIFAR-10 进行预处理，然后将这些变化可视化出来。CIFAR-10 训练集的大小是 50000 x 3072，其中每张图片都可以拉伸为 3072 维的行向量。我们可以计算 [ 3072 x 3072 ] 的协方差矩阵然后进行奇异值分解（比较耗费计算性能）

第一张：一个用于演示的集合，含49张图片
第二张：3072 个特征值向量中的前 144 个。靠前面的特征向量解释了数据中大部分的方差，可以看见它们与图像中较低的频率相关
第三张：49 张经过了 PCA 降维处理的图片，展示了 144 个特征向量。这就是说，第一张里面用于展示的原始图像是每个图像用 3072 维的向量，向量中的元素是图片上某个位置的像素在某个颜色通道中的亮度值。而现在每张图片只使用了一个 144 维的向量，其中每个元素表示了特征向量对于组成这张图片的贡献度。为了让图片能够正常显示，需要将 144 维度重新变成基于像素基准的 3072 个数值。因为 U 是一个旋转，可以通过乘以 U.transpose()[:144,:] 来实现，然后将得到的 3072 个数值可视化。可以看见图像变得有点模糊了，这正好说明前面的特征向量获取了较低的频率。然而，大多数信息还是保留了下来
第四张：将白化后的数据进行显示。其中 144 个维度中的方差都被压缩到了相同的数值范围。然后 144 个白化后的数值通过乘以 U.transpose()[:144,:] 转换到图像像素基准上。现在较低的频率（代表了大多数方差）可以忽略不计了，较高的频率（代表相对少的方差）就被夸大了

注，实际上在卷积神经网络中并不会采用 PCA 和白化。然而对数据进行零中心化操作还是非常重要的，对每个像素进行归一化也很常见

权重初始化

全零初始化

首先应该指出，全零初始化时错误的，因为如果网络中的每个神经元都计算出同样的的输出，然后它们在反向传播时就会计算出同样的梯度，从而进行同样的参数更新。换句话说，如果权重被初始化为同样的值，神经元之间就失去了不对称性的源头

小随机数初始化

因此，权重初始值要非常接近 0 有不能等于 0，解决方法是将权重初始化为很小的数字，以此来打破对称性。其思路是：如果神经元刚开始的时候是随机且不相等的，那么他们将计算出不同的更新，并将自身变成整个网络的不同部分

小随机数权重初始化的实现方式：W=0.01*np.random.randn(D,H)，randn 函数是基于零均值和标准差的一个高斯分布来生成随机数。根据这个式子，每个神经元的权重向量都被初始化为一个随机向量，而这些随机向量又服从一个多变量高斯分布，这样在输入空间中，所有的神经元的指向是随机的

注意，并不是小数值一定会得到好结果，一个神经网络层的权重值很小，那么反向传播就会计算出非常小的梯度，这会很大程度上减小反向传播中的梯度信号，进而在深度网络中导致梯度消失的问题

使用 1/sqrt(n) 标准方差

上面做法存在一个问题，随着输入数据量的增长，随机初始化的神经元的输出数据的分布中的方差也在增大。我们可以除以输入数据量的平方根来调整其数字范围，这样神经元输出的方差就归一化了，即 w=np.random.randn(n)/sqrt(n)

这样就保证了网络中所有神经元起始时有近似同样额度输出分布。实践经验证明，这样做可以提高收敛的速度

上述结论的推导过程如下：

假设权重 $w$ 和输入 $x$ 之间的内积为 $\sum_i^nw_ix_i$ ，这是还没有进行非线性激活函数运算之前的原始数值

我们可以检查 $s$ 的方差

$Var(s)=Var(\sum_i^nw_ix_i)$
$=\sum_i^nVar(w_ix_i)$
$=\sum_i^n[E(w_i)]^2Var(x_i)+E[(x_i)]^2Var(w_i)+Var(xI_i)Var(w_i)$
$=\sum_i^nVar(x_i)Var(w_i)$
$= (n V a r (w)) V a r (x)$

在前两步，使用了方差的性质。在第三步，因为假设输入和权重的平均值都是 0，所以 $E[x_i]=E[w_i]=0$ 。注意这并不是一般化的情况，比如在 ReLU 单元中均值就为正。在最后一步，我们假设所有的 $w_i,x_i$ 都服从同样的分布

从这个推导过程我们可以看到，如果想要 $s$ 有何输入 $x$ 一样的方差，那么在初始化的时候必须保证每个权重 $w$ 的方差是 $1 / n$ 。又因为对于一个随机变量 $X$ 和标量 $a$ ，有 $Var(aX)=a^2Var(x)$ ，这就说明可以基于一个标准高斯分布，然后乘以 $a=\sqrt{1/n}$ ，使其方差为 $1 / n$ ，于是得出结论：w=np.random.randn(n)/sqrt(n)

另外，对于 ReLU 激活函数，推荐使用 w=np.random.randn(n)*sqrt(2.0/n) 来进行权重初始化，有论文指出使用 ReLU 激活时审计员的方差是 $2.0 / n$

稀疏初始化

另一个处理非标定方差的方法是将所有权重矩阵设为 0，但是为了打破对称性，每个神经元都同下一层固定数目的神经元随机连接（其权重数值由一个小的高斯分布生成）

偏置的初始化

通常将偏置初始化为 0，这是因为随机小数值权重矩阵已经打破了对称性。对于 ReLU 非线性激活函数，有研究人员喜欢使用如 0.01 这样的小数值常量作为所有偏置的初始值，这是因为他们认为这样做能让所有 ReLU 单元一开始就激活，这样就能保存并传播一些梯度。然而这样做是不是总能提高算法性能暂不清楚，所以通常还是使用 0 来初始化偏置参数

批量归一化

批量归一化的做法是让激活数据在训练开始前通过一个网络层，该网络层处理数据使其服从标准高斯分布。在实现层面，应用这个技巧通常意味着全连接层，或者是卷积层与激活函数之间添加一个 BatchNorm 层。在实践中，使用了批量归一化的网络对于不好的初始值有更强的鲁棒性

神经网络的正则化

L2 正则化

L2 正则化是最常用的正则化方法，以防止网络过拟合。可以通过乘法目标函数中所有参数的平方实现，即对于网络中的每个权重 $w$ ，向目标函数中添加一个 $\frac{1}{2}\lambda w^2$ ，其中 $\lambda$ 是正则化强度，系数 $1 / 2$ 是因为加上后该式子关于 $w$ 的梯度就是 $\lambda w$ 而不是 $2\lambda w$

L2 正则化可以直观理解为它对于大数值的权值向量进行严厉惩罚，倾向于更加分散权重向量

在梯度下降和参数更新的时候，使用 L2 正则化一位着所有的权重都以 w+=-lambda*w 向着 0 线性下降

L1 正则化

对于每个 $w$ 我们都向目标函数增加一个 $\lambda|w|$ ，L1 和 L2 正则化也可以进行组合， $\lambda_1|w|+\lambda_2w^2$

L1 正则化有一个有趣大的性质，它会让权重向量在最优化的过程中变得稀疏（即非常接近 0）。也就是说，使用 L1 正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集，同时对于噪音输入则几乎是不变的了

在实践中，如果不是特别关注某些明确的特征选择，一般说来 L2 正则化都会比 L1 正则化效果好

最大范式约束

另一种形式的正则化是给每个神经元中权重向量的量级设定上限，并使用投影梯度下降来确保这一约束。在实践中，与之对应的是参数更新方式不变，然后要求神经元中的权重向量 $\vec w$ 必须满足 $||\vec w||_2∣∣w ∣∣2<c$

这种正则化还有一个良好的性质，即使在学习率设置过高的时候，网络中也不会出现数值爆炸，因为它的参数更新始终是被限制着的

随机失活

在训练的时候，随机失活的实现方法是让神经元以超参数 $p$ 的概率被激活或者被置为 0

上述操作不好的性质是必须在测试时对激活数据按照 $p$ 进行数字范围调整。例如， $p = 0.5$ ，在测试时神经元必须把它们的输出减半，这是因为在训练的时候它们的输出只有一半。先假设有一个神经元 $x$ 的输出，那么进行随机失活的时候，该神经元的输出就是 $px+(1-p)\cdot0$ ，有 $1 - p$ 的概率神经元的输出为 $0$ 。在测试时神经元总是激活的，就必须调整 $x\rightarrow px$ 来保持同样的预期输出

既然测试性能如此关键，实际更倾向于使用 『反向随机失活（inverted dropout）』，它在训练时就进行数字范围调整，从而让前向传播在测试时保持不变。这样做还有一个好处，无论你决定是否使用随机失活，预测方法的代码可以保持不变

前向传播中的噪音

在更一般化的分类上，随机失活属于网络在前向传播中有随机行为的方法。测试时，通过分析法（在使用随机失活中就乘以 $p$ ）或数值法（例如通过抽样出很多子网络，随机选择不同子网络进行前向传播，最后对它们去平均）将噪音边缘化。在这个方向上的另一个研究是 DropConnect，它在前向传播的时候，一系列权重被随机设置为 0

偏置正则化

在线性分类器的章节中介绍过，对于偏置参数的正则化并不常见，因为它们在矩阵乘法中和输入数据并不产生互动，所以并不需要控制其在数据维度上的效果。然而在实际应用中（使用了合理数据预处理的情况下），对偏置进行正则化也很少会导致算法性能变差。这可能是因为相较于权重参数，偏置参数实在太少，所以分类器需要它们来获得一个很好的数据损失，那么还是能够承受的

神经网络的损失函数

分类问题

在该问题中，假设有一个装满样本的数据集，每个样本都有一个唯一的正确标签。在这类问题中，一个最常见的损失函数就是 SVM： $L_i=\sum_{j\neq y_i}max(0,f_j-f_{y_i}+1)$
第二个常用的损失函数是 Softmax 分类器，它使用交叉熵损失： $L_i=-log\left ( \frac{e^{f_{y_i}}}{\sum_je^{f_j}} \right )$

当标签集非常大时，就需要使用分层 Softmax，它将标签分解成一棵树，每个标签都表示成这个树上的一个路径，这个树的每个结点都训练一个 Softmax 分类器来在左右分支之间做决策。树的结果对于算法的最终结果影响很大，而且一般需要具体问题具体分析

属性分类

上面分类问题的损失函数都是假设每个样本只有一个正确的标签 $y_i$ ，但是如果 $y_i$ 是一个二值向量，每个样本可能有，也可能没有某个属性，而且属性之间并不相互排斥呢？

在这种情况下，不错的做法是为每个属性创建一个独立的二分类的分类器。例如，针对每个分类的二分类器会采用下面的公式： $L_i=\sum_jmax(0,1-y_{ij}f_j)$ 其中，求和是对所有分类 $j$ ， $y_{ij}$ 的值为 1 或 -1，具体根据第 $i$ 个样本是否被第 $j$ 个属性打标签而决定，当该类别被正确预测时，分值向量 $f_j$ 为正，其余情况为负。可以发现，当一个正样本的得分小于 +1，或者一个负样本得分大于 -1 的时候，就会累积损失值

另一种方法是对每种属性训练一个独立的逻辑回归分类器。二分类的逻辑回归分类器只有两个分类 $(0, 1)$ ，其中对于分类 $1$ 的概率为： $P(y=1|x;w,b)=\frac{1}{1+e^{-(w^Tx+b)}}=\sigma(w^Tx+b)$
因为类别 $0$ 和类别 $1$ 的概率和为 1，所以类别 $0$ 的概率为 $P (y = 0 ∣ x; w, b) = 1 - P (y = 1 ∣ x; w, b)$ 。这样如果 $\sigma(w^Tx+b)>0.5$ 或者 $w^Tx+b>0$ ，那么样本就要被分类成为正样本（ $y = 1$ ）

然后，损失函数最大化这个对数似然函数，问题可以简化为 $L_i=\sum_jy_{ij}log\sigma(f_j)+(1-y_{ij})log(1-\sigma(f_j))$ 其中， $\sigma(\cdot)$ 就是 sigmoid 函数。虽然上面的公式看起来吓人，但是 $f$ 的梯度实际上非常简单： $\frac{\partial L_i}{\partial f_i}=y_{ij}-\sigma(f_j)$

回归问题

回归问题是预测实数值的问题，比如房价。对于这种问题，通常是计算预测值和真实值之间的损失。然后用 L2 平方范式或 L1 范式度量差异，对于某个样本，L2 范式计算如下： $L_i=||f-y_i||_2^2$ 之所以在目标函数中要进行平方，是因为梯度算起来更加简单。因为平方是一个单调运算，所以不用改变最优参数。L1 范式则是将每个维度上的绝对值加起来： $L_i=||f-y_i||_1=\sum_j|f_j-(y_i)_j|$ 观察第 $i$ 个样本的第 $j$ 维，用 $\delta_{ij}$ 表示预测值与真实值之间的差异。关于该维度的梯度，即 $\partial L_i/\partial f_j$ 能够轻松地求导为 L2 范式的 $\delta_{ij}$ 或 $sign(\delta_{ij})$ 。这也就是说，评分值的梯度要么与误差中的差值直接成比例，要么是固定的并从差值中继承 $s i g n$

L2 损失比起较为稳定的 Softmax 损失来，其最优化过程要困难很多。直观而言，它需要网络具备一个特别的性质，即对于每个输入（和增量）都要输出一个确切的正确值。而在 Softmax 中就不是这样，每个评分的准确值并不是那么重要：只有当它们量级适当的时候，才有意义。还有，L2损失鲁棒性不好，因为异常值可以导致很大的梯度。所以在面对一个回归问题时，先考虑将输出变成二值化是否真的不够用。例如，如果对一个产品的星级进行预测，使用 5 个独立的分类器来对 1 - 5 星进行打分的效果一般比使用一个回归损失要好很多。分类还有一个额外优点，就是能给出关于回归的输出的分布，而不是一个简单的毫无把握的输出值。如果确信分类不适用，那么使用 L2 损失吧，但是一定要谨慎：L2 非常脆弱，在网络中使用随机失活（尤其是在 L2 损失层的上一层）不是好主意

结构化预测

结构化损失是指标签可以是任意的结构，例如图表、树或者其他复杂的情况。通常这种情况还会假设结构空间非常巨大，不容易进行遍历。结构化 SVM 背后的基本思想就是在正确的结构 $y_i$ 和得分最高的非正确结构之间画出一个边界。解决这类问题，并不是像解决一个简单无限制的最优化问题那样使用梯度下降就可以了，而是需要设计一些特殊的解决方案，这样可以有效利用对于结构空间的特殊简化假设

梯度检查

理论上进行梯度检查很简单，就是把解析梯度和数值计算梯度进行比较。然而从实际操作层面上讲，这个过程复杂且易出错。下面是一些提示、技巧和需要注意的事情、

使用中心化公式

在使用优先差值近似来计算数值梯度的时候，常见的公式是： $\frac{df(x)}{dx}=\frac{f(x+h)-f(x)}{h}$ 其中 $h$ 是一个很小的数字，在实践中近似为 1e-5，但是在实践中使用中心化公式效果更好 $\frac{df(x)}{dx}=\frac{f(x+h)-f(x-h)}{2h}$ 该公式在检查梯度的每个维度的时候，会要求计算两次损失函数，但是梯度的近似值会准确很多。要理解这一点，对 $f (x + h)$ 和 $f (x - h)$ 使用泰勒展开，可以看到第一个公式的误差近似 $O (h)$ ，第二个公式的误差近似 $O(h^2)$

使用相对误差来比较

比较数值梯度 $f'_n$ 和解析梯度 $f'_a$ 可能会倾向于监测它们的差的绝对值 $f'_a-f'_h|$ 或者差的平方值，然后定义该值如果超过某个规定阈值，就判断梯度实现失败

然而，该思路是有问题。想想，假设这个差值是 1e-4，如果两个梯度值在 1.0 左右，这个差值看起来就很合适，可以认为两个梯度是匹配的。然而，如果梯度值是 1e-5 或者更低，那么 1e-4 就是非常大的差距，梯度实现肯定就是失败的了。因此，使用相对误差总是更合适一些： $\frac{|f'_a-f'_n|}{max(|f'_a|,|f'_n|)}$ 上式考虑了差值占两个梯度绝对值的比例

通常相对误差公式质包含两个式子中的一个，但是我们更倾向于取两个式子的最大值或者取两个式子的和。这样做是为了防止在其中一个式子为 0 时，分母变为 0（这种情况在 ReLU 中经常发生）。然而，还必须注意两个式子都为零且通过梯度检查的情况。在实践中，

相对误差 > 1e-2：通常意味着梯度可能出错
1e-2 > 相对误差 > 1e-4：这个值还是有点问题
1e-4 > 相对误差：这个值的相对误差对于有不可导点的目标函数还是 ok 的，如果目标函数中没有 kink（使用 tanh 和 Softmax），那么相对误差值还是太高
1e-7 或者更小：好结果

要知道，网络的深度越大，相对误差就越高。所以如果你是在对一个十层网络的输入数据做梯度检查，那么 1e-2 的相对误差可能就还行。相反，如果一个可微函数的相对误差值为 1e-2，那么通常说明梯度实现不正确

使用双精度

一个常见的错误就会说使用单精度浮点数来进行梯度检查。这样会导致即使梯度实现正确，相对误差值也会很高

保持在浮点数的有效范围

在神经网络中，在一个批量的数据上对损失函数进行归一化是很常见的。但是，如果每个数据点的梯度很小，然后又用数据点的数量去除，就使得数值更小，这样反过来会导致更多的数值问题。在实践时总是把原始的解析梯度和数值梯度数据打印出来，确保用来比较的数字的值不会过小（通常绝对值小于 1e-10 就不太好）。如果确实过小，可以使用一个常数暂时将损失函数的数值范围扩展到一个更好的范围

目标函数的不可导点（kinks）

在进行梯度检查时，一个导致不准确的原因是不可导点。例如，当 $x = - 1 e 6$ 时，对 ReLU 函数进行梯度检查。因为 $x < 0$ ，所以解析梯度在该点的梯度为 $0$ 。然而，在这里数值梯度会突然计算出一个非零的梯度值，因为 $f (x + h)$ 可能越过了不可导点，导致了一个非零的结果

可能会认为这是一个极端的案例，但实际上这种情况很常见。例如，一个用 CIFAR-10 训练的 SVM 中，因为有 50,000 个样本，且根据目标函数每个样本产生 9 个式子，所以包含有 450,000 个 $m a x (0, x)$ 式子。而一个用 SVM 进行分类的神经网络因为采用了 ReLU，还会有更多的不可导点

使用少量数据点

解决上面的不可导点问题的一个办法是使用更少的数据点。因为含有不可导点的损失函数的数据点越少，不可导点就越少，所以在计算优先差值近似时越过不可导点的几率就越小。另外，如果你的梯度检查对 2 - 3 个数据点都有效，那么基本上对整个批量数据进行提督检查也是没问题的。所以使用少量的数据点，能让梯度检查更迅速高效

谨慎设置步长 h

在实践中 $h$ 并不是越小越好，因为当 $h$ 特别小的时候，就可能会遇到数值精度问题。有时候如果梯度检查无法进行，可以试试将 $h$ 调到 1e-4 或者 1e-6，然后突然梯度检查可能就恢复正常

在操作的特性模式中进行梯度检查

梯度检查是在参数空间中的一个特定的单独点进行。即使是在该点上梯度检查成功了，也不能马上确保全局上梯度的实现都是正确的的

另外，一个随机的初始化可能不是参数空间最优代表性的点，这可能导致进入某种病态的情况，即梯度看起来是正确实现了，实际上却并没有

例如，SVM 使用小数值权重初始化，就会把一些接近于 0 的得分分配给所有的数据点，而梯度将会在所有的数据点上展现出某种模式。一个不正确实现的梯度也许依然能够产生出这种模式，但是不能泛化到更具代表性的操作模式，比如在一些得分比另一些得分更大的情况下就不行。因此为了安全起见，最好让网络学习（ “ 预热 ” ）一小段时间，等到损失函数开始下降之后再进行梯度检查。第一次迭代就进行梯度检查的危险就在于，此时可能正处在不正常的边界情况，从而掩盖了梯度没有正确实现的事实

不要让正则化吞没数据

通常损失函数是数据损失和正则化损失的和（例如 L2 对权重的惩罚）。需要注意的是，正则化损失可能吞没掉数据损失，在这种情况下梯度主要来源于正则化部分。这样就会掩盖掉数据损失梯度的不正确实现。因此，推荐先关掉正则化对数据损失做单独检查，然后对正则化做单独检查。对于正则化的单独检查可以是修改代码，去掉其中数据损失的部分，也可以提高正则化强度，确认其效果在梯度检查中是无法忽略的，这样不正确的实现就会被观察到了

记得关闭随机失活和数据扩张（augmentation）

在进行梯度检查时，记得关闭网络中任何不确定效果的操作，比如随机失活，或者随机数据扩展等。不然它们会在计算数值梯度的时候导致巨大误差。关闭这些操作不好的一点是无法对它们进行梯度检查（例如随机失活的反向传播实现可能出现错误）。因此，一个更好的解决方案就是在计算 $f (x + h)$ 和 $f (x - h)$ 前强制增加一个特定的随机种子，在计算解析梯度时也同样如此

检查少量的维度

在实际中，梯度可以有上百万的参数，在这种情况下只能检查其中一些维度然后假设其他维度是正确的。注意，确认在所有不同的参数中都抽取一部分来梯度检查。在某些应用中，为了方便，人们将所有的参数放到一个巨大的参数向量中。在这种情况下，例如，偏置就可能只占用整个向量中的很小一部分，所以不要随机地从向量中取维度，一定要把这种情况考虑到，确保所有参数都收到了正确的梯度

合理性检查

在进行最优化之前，最好进行一些合理性检查

寻找特定情况的正确损失值

在使用小参数进行初始化时，确保得到的损失值与期望一致。最好先单独检查数据损失（让正则化强度为 0 ）。例如，对于一个 CIFAR-10 的 Softmax 分类器，一般期望它的初始损失值是 2.302，这是因为初始时预计每个类别的概率是 0.1（因为有 10 个类别），然后 Softmax 损失值正确分类的负对数概率：-ln(0.1) = 2.302。对于 Weston Watkins SVM，假设所有的边界都被越过（因为所有的分值都近似为零），所以损失值是 9（因为对于每个错误分类，边界值是1）。如果没看到这些损失值，那么初始化中就可能有问题

第二个合理性检查

提高正则化强度时导致损失值变大

对小数据子集过拟合

最后一步也是最重要的一步，在整个数据集进行训练之前，尝试在一个很小的数据集上进行训练（比如 20 个数据），然后确保能到达 0 的损失值。进行这个实验的时候，最好让正则化强度为 0，不然它会阻止得到 0 的损失。除非能通过这一个正常性检查，不然进行整个数据集训练是没有意义的。但是注意，能对小数据集进行过拟合并不代表万事大吉，依然有可能存在不正确的实现。比如，因为某些错误，数据点的特征是随机的，这样算法也可能对小数据进行过拟合，但是在整个数据集上跑算法的时候，就没有任何泛化能力

检查整个学习过程

在训练神经网络的时候，应该跟踪多个重要数值。这些数值输出的图表是观察训练进程的一扇窗口，是直观理解不同的超参数设置效果的工具，从而知道如何修改超参数以获得更高效的学习过程

在下面的图表中，x 轴通常都是表示 『周期（epochs）单位』，该单位衡量了在训练中每个样本数据都被观察过次数的期望（一个周期意味着每个样本数据都被观察过了一次）。相较于迭代次数（iterations），一般更倾向跟踪周期，这是因为迭代次数与数据的批尺寸有关，而批尺寸的设置又可以是任意的

损失函数

训练期间第一个要跟踪的数值就是损失值，它在前向传播时对每个独立的批数据进行计算。下图展示的是随着损失值随时间的变化，尤其是曲线形状会给出关于学习率设置的情况：

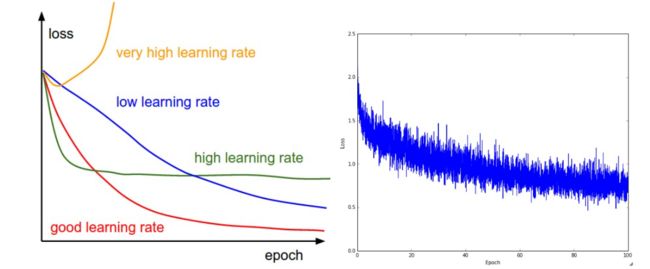
损失值的震荡程度和批尺寸有关，当批尺寸为 1，震荡会相对较大。当批尺寸就是整个数据集时震荡就会最小，因为每个梯度更新都是单调地优化损失函数（除非学习率设置得过高）

有的研究者喜欢用对数域对损失函数值作图。因为学习过程一般都是采用指数型的形状，图表就会看起来更像是能够直观理解的直线，而不是呈曲棍球一样的曲线状。还有，如果多个交叉验证模型在一个图上同时输出图像，它们之间的差异就会比较明显

训练集和验证集准确率

在训练分类器的时候，需要跟踪的第二重要的数值是验证集和训练集的准确率。这个图表能够展现知道模型过拟合的程度：

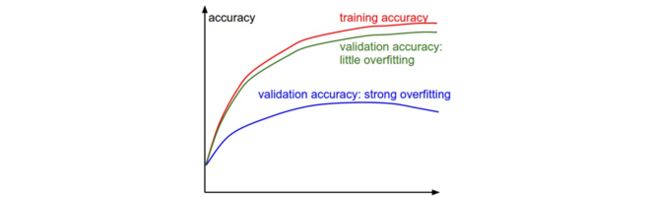
在训练集准确率和验证集准确率中间的空隙指明了模型过拟合的程度。在图中，蓝色的验证集曲线相较于训练集曲线，验证集的准确率低了很多，这就说明模型有很强的过拟合。遇到这种情况，就应该增大正则化强度（更强的 L2 权重惩罚，更多的随机失活等）或收集更多的数据。另一种可能是验证集曲线和训练集曲线如影随形，这种情况说明你的模型容量还不够大：应该通过增加参数数量让模型容量更大些

权重更新比例

最后一个应该跟踪的量是权重中更新值的数量和全部值的数量之间的比例。注意，是更新的，而不是原始梯度。需要对每个参数集的更新比例进行单独的计算和跟踪。一个经验性的结论是这个比例应该在 1e-3 左右。如果更低，说明学习率可能太小，如果更高，说明学习率可能太高

每层的激活数据及其梯度分布

一个不正确的初始化可能让学习过程变慢，甚至彻底停止。还好，这个问题可以比较简单地诊断出来。其中一个方法是输出网络中所有层的激活数据和梯度分布的柱状图。直观地说，就是如果看到任何奇怪的分布情况，那都不是好兆头。比如，对于使用 tanh 的神经元，我们应该看到激活数据的值在整个 [ -1, 1 ] 区间中都有分布。如果看到神经元的输出全部是 0，或者全都饱和了往 -1 和 1 上跑，那肯定就是有问题了

第一层可视化

最后，如果数据是图像像素数据，那么把第一层特征可视化会有帮助

左图中的特征充满了噪音，这暗示了网络可能出现了问题：网络没有收敛，学习率设置不恰当，正则化惩罚的权重过低等。右图的特征不错，平滑，干净而且种类繁多，说明训练过程进行良好

参数更新

随机梯度下降

普通更新

最简单的更新形式是沿着负梯度方向改变参数。假设有一个参数向量 x 及其梯度 dx，那么最简单的更新形式是：

# 普通更新
x += - learning_rate * dx

其中 learning_rate 是一个超参数，它是一个固定的常量。当在整个数据集上进行计算时，只要学习率足够低，总是能在损失函数上得到非负的进展

动量更新

这个方法在深度网络上几乎总能得到更好的收敛速度。该方法可以看成是从物理角度上对于最优化问题得到的启发。损失值可以理解为山的高度，因此，高度势能是 $U = m g h$ ，所以 $U\propto h$ 。用随机数字初始化参数等同于在某个位置给字典设定初始速度为 0。这样最优化过程可以看做是模拟参数向量（即质点）在地形上滚动的过程

因为作用于质点的力与梯度的潜在能量（ $F = - U$ ）有关，质点所受的力就是损失函数的负梯度。另外，因为 $F = m a$ ，所以在这个观点下负梯度与质点的加速度成正比。注意，在普通版本中，梯度直接影响位置；而在动量更新中，从物理观点来理解，梯度只是影响速度，然后速度再影响位置

# 动量更新
v = mu * v - learning_rate * dx # 与速度融合
x += v # 与位置融合

在这里引入了一个初始化为 0 的变量 v 和一个超参数 mu，这个变量 mu 在最优化的过程中被看作是动量（一般值设为 0.9），但其物理意义与摩擦系数更一致。这个变量有效地一直了速度，降低了系统的动能，不然字典在山底永远不会停下来。通过交叉验证，这个参数通常设为 [ 0.5, 0.9, 0.95, 0.99 ] 中的一个。和学习率随着时间退货类似，动量随时间变化的设置有时能略微改善最优化的效果，其中动量在学习过程的后阶段会上升。一个典型的设置是刚开始将动量设为 0.5，而后面的多个周期中慢慢提升到 0.99

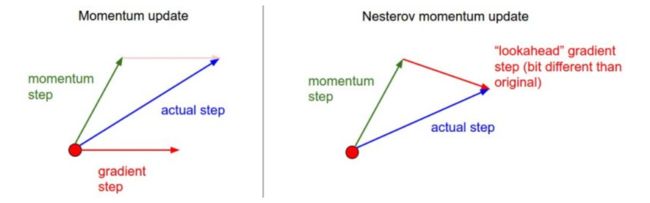
Nesterov 动量

在理论上，Nesterov 对于凸函数能得到更好的收敛，在实践中也确实比标准动量表现更好一些

Nesterov 动量的核心思路是：当参数向量位于某个位置 x 时，观察上面的动量更新公式可以发现，动量部分（忽视带梯度的第二个部分）会通过 mu * v稍微改变参数向量。因此，如果要计算梯度，那么可以将未来的近似位置 x + mu * v看做是向前看，这个点在我们一会儿要停止的位置附近。因此，计算 x + mu * v的梯度而不是旧位置 x 的梯度就有意义了

x_ahead = x + mu * v
# 计算dx_ahead(在x_ahead处的梯度，而不是在x处的梯度)
v = mu * v - learning_rate * dx_ahead
x += v

然而在实践中，人们更喜欢和普通 SGD 或上面的动量方法一样简单的表达式。通过对 x_ahead = x + mu * v 使用变量变换进行改写是可以做到的，然后用 x_ahead 而不是 x 来表示上面的更新。也就是说，实际存储的参数向量总是向前一步的那个版本。x_ahead 的公式（将其重新命名为 x ）就变成了：

v_prev = v # 存储备份
v = mu * v - learning_rate * dx # 速度更新保持不变
x += -mu * v_prev + (1 + mu) * v # 位置更新变了形式

学习率退火

在训练深度网络的时候，让学习率随着时间退火通常是有帮助的。可以这样理解：如果学习率很高，系统的动能就过大，参数向量就会无规律地跳动，不能够稳定到损失函数更深更窄的部分去。知道什么时候开始衰减学习率是有技巧的：慢慢减小它，可能在很长时间内只能是浪费计算资源地看着它混沌地跳动，实际进展很少。但如果快速地减少它，系统可能过快地失去能量，不能到达原本可以到达的最好位置。通常，实现学习率退火有 3 种方式：

随步树衰减：每进行几个周期就根据一些因素降低学习率。典型的值是每过 5 个周期就将学习率减少一半，或者每 20 个周期减少到之前的 0.1。这些数值的设定是严重依赖具体问题和模型的选择的。在实践中可能看见这么一种经验做法：使用一个固定的学习率来进行训练的同时观察验证集错误率，每当验证集错误率停止下降，就乘以一个常数（比如 0.5）来降低学习率
指数衰减：根据数学公式 $\alpha=\alpha_0e^{-kt}$ ，其中 $\alpha_0,k$ 是超参数， $t$ 是迭代次数
1/t 衰减：根据数学公式 $\alpha=\alpha_0/(1+kt)$ ，其中 $\alpha_0,k$ 是超参数， $t$ 是迭代次数

在实践中，我们发现随步数衰减的随机失活（dropout）更受欢迎，因为它使用的超参数（衰减系数和以周期为时间单位的步数）比 $k$ 更有解释性。最后，如果你有足够的计算资源，可以让衰减更加缓慢一些，让训练时间更长些

二阶方法

在深度网络背景下，第二类常用的最优化方法是基于牛顿法的，其迭代如下： $x\leftarrow x-[Hf(x)]^{-1}\triangledown f(x)$ 这里 $H f (x)$ 是 Hessian 矩阵，它是函数的二阶偏导数的平方矩阵； $\triangledown f(x)$ 是梯度向量，这和梯度下降中一样。直观理解上， Hessian 矩阵描述了损失函数的局部曲率，从而使得可以进行更高效的参数更新。具体来说，就是乘以 Hessian 转置矩阵可以让最优化过程在曲率小的时候大步前进，在曲率大的时候小步前进。需要重点注意的是，在这个公式中是没有学习率这个超参数的，这相较于一阶方法是一个巨大的优势

然而上述更新方法很难运用到实际的深度学习应用中去，这是因为计算（以及求逆） Hessian 矩阵操作非常耗费时间和空间。举例来说，假设一个有一百万个参数的神经网络，其 Hessian 矩阵大小就是 [1,000,000 x 1,000,000 ]，将占用将近 3725GB 的内存。这样，各种各样的拟-牛顿法就被发明出来用于近似转置 Hessian 矩阵。在这些方法中最流行的是L-BFGS，该方法使用随时间的梯度中的信息来隐式地近似（也就是说整个矩阵是从来没有被计算的）

然而，即使解决了存储空间的问题，L-BFGS 应用的一个巨大劣势是需要对整个训练集进行计算，而整个训练集一般包含几百万的样本。和小批量随机梯度下降（mini-batch SGD）不同，让 L-BFGS 在小批量上运行起来是很需要技巧，同时也是研究热点

在深度学习和卷积神经网络中，使用 L-BFGS 之类的二阶方法并不常见。相反，基于Nesterov 的动量更新的各种随机梯度下降方法更加常用，因为它们更加简单且容易扩展

逐参数适应学习率方法

前面讨论的所有方法都是对学习率进行全局地操作，并且对所有的参数都是一样的。学习率调参是很耗费计算资源的过程，所以很多工作投入到发明能够适应性地对学习率调参的方法，甚至是逐个参数适应学习率调参。很多这些方法依然需要其他的超参数设置，但是其观点是这些方法对于更广范围的超参数比原始的学习率方法有更良好的表现。在本小节我们会介绍一些在实践中可能会遇到的常用适应算法

Adagrad

# 假设有梯度和参数向量x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

注意，变量 cache 的尺寸和梯度矩阵的尺寸是一样的，还跟踪了每个参数的梯度的平方和。这个一会儿将用来归一化参数更新步长，归一化是逐元素进行的。另外，接收到高梯度值的权重更新的效果被减弱，而接收到低梯度值的权重的更新效果将会增强。有趣的是平方根的操作非常重要，如果去掉，算法的表现将会糟糕很多。用于平滑的式子 eps（一般设为 1e-4 到 1e-8 之间）是防止出现除以 0 的情况

Adagrad 的一个缺点是，在深度学习中单调的学习率被证明通常过于激进且过早停止学习

RMSprop

是一个非常高效，但没有公开发表的适应性学习率方法。有趣的是，每个使用这个方法的人在他们的论文中都引用自 Geoff Hinton 的 Coursera 课程的第六课的第 29 页 PPT

这个方法用一种很简单的方式修改了 Adagrad 方法，让它不那么激进，同时也单调地降低了学习率。具体说来，就是它使用了一个梯度平方的滑动平均：

cache =  decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

在上面的代码中，decay_rate 是一个超参数，常用的值是 [ 0.9, 0.99, 0.999 ]，其中 x+= 和 Adagrad 中是一样的，但是 cache 变量却是不同的。因此，RMSProp 仍然是基于梯度的大小来对每个权重的学习率进行修改，这样的效果还是不错。但是和 Adagrad 不同，其更新不会让学习率单调变小

Adam

它看起来像是RMSProp的动量版。简化的代码是下面这样

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

注意这个更新方法看起来和 RMSProp 很像，其使用的是平滑版的梯度 m，而不是用的原始梯度向量 dx。论文中推荐的参数值 eps = 1e-8，beta1 = 0.9，beta2 = 0.999

在实际操作中，我们推荐 Adam 作为默认的算法，一般而言跑起来比 RMSProp 要好一点。但是也可以试试 SGD + Nesterov 动量。完整的 Adam 更新算法也包含了一个偏置矫正机制，因为 m、v 两个矩阵初始为 0，在没有完全热身之前存在偏差，需要采取一些补偿措施

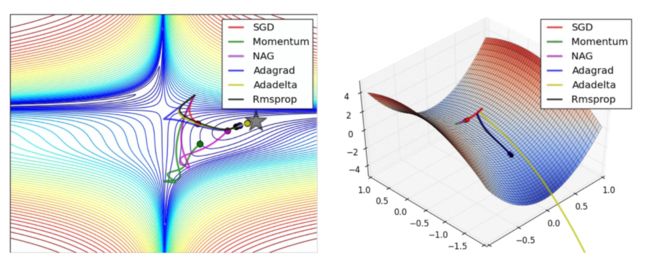
针对上面右边的图作出一点解释，我们可以发现 SGD 很难突破对称性，一直卡在顶部。而 RMSProp 之类的方法能够看到马鞍方向有很低的梯度。因为在 RMSProp 更新方法中的分母项提高了在该方向的有效学习率，使得 RMSProp 能够继续前进

超参数调优

我们已经看到，训练一个神经网络会遇到很多超参数设置。神经网络最常用的设置有：

初始学习率
学习率衰减方式，例如一个衰减常量
正则化强度，如 L2 惩罚，随机失活强度

更大的神经网络需要更长的时间去训练，所以调参可能需要几天甚至几周。记住这一点很重要，因为这会影响你设计代码的思路。一个具体的设计是用仆程序持续地随机设置参数然后进行最优化。在训练过程中，仆程序会对每个周期后验证集的准确率进行监控，然后向文件系统写下一个模型的记录点（记录点中有各种各样的训练统计数据，比如随着时间的损失值变化等），这个文件系统最好是可共享的。在文件名中最好包含验证集的算法表现，这样就能方便地查找和排序了。然后还有一个主程序，它可以启动或者结束计算集群中的仆程序，有时候也可能根据条件查看仆程序写下的记录点，输出它们的训练统计数据等

在大多数情况下，一个尺寸合理的验证集可以让代码更简单，不需要用几个数据集来交叉验证。你可能会听到人们说他们交叉验证一个参数，但是大多数情况下，他们实际是使用的一个验证集

对于超参数的范围，我们一般在对数尺度上进行超参数搜索。例如，一个典型的学习率应该看起来是这样：learning_rate = 10 ** uniform(-6, 1)，也就是说，我们从标准分布中随机生成了一个数字，然后让它成为 10 的阶数

对于正则化强度，可以采用同样的策略。直观地说，这是因为学习率和正则化强度都对于训练的动态进程有乘的效果。例如：当学习率是 0.001 的时候，如果对其固定地增加 0.01，那么对于学习进程会有很大影响。然而，当学习率是 10 的时候，影响就微乎其微了。这是因为学习率乘以了计算出的梯度。因此，比起加上或者减少某些值，思考学习率的范围是乘以或者除以某些值更加自然。但是有一些参数（比如随机失活）还是在原始尺度上进行搜索。例如：dropout=uniform(0,1)

通常，有些超参数比其余的更重要，通过随机搜索，而不是网格化的搜索，可以让你更精确地发现那些比较重要的超参数的好数值

对于边界上的最优值要小心。这种情况一般发生在一个不好的范围内搜索超参数的时候。比如，假设我们使用 learning_rate = 10 ** uniform(-6,1) 来进行搜索。一旦我们得到一个比较好的值，一定要确认你的值不是出于这个范围的边界上，不然你可能错过更好的其他搜索范围

从粗到细地分阶段搜索。在实践中，先进行初略范围（比如10 ** [-6, 1]）搜索，然后根据好的结果出现的地方，缩小范围进行搜索。进行粗搜索的时候，让模型训练一个周期就可以了，因为很多超参数的设定会让模型没法学习，或者突然就爆出很大的损失值。第二个阶段就是对一个更小的范围进行搜索，这时可以让模型运行 5 个周期，而最后一个阶段就在最终的范围内进行仔细搜索

贝叶斯超参数最优化是一整个研究领域，主要是研究在超参数空间中更高效的导航算法。其核心的思路是在不同超参数设置下查看算法性能时，要在探索和使用中进行合理的权衡。基于这些模型，发展出很多的库，比较有名的有： Spearmint，SMAC，和 Hyperopt。然而，在卷积神经网络的实际使用中，比起上面介绍的先认真挑选一个范围，然后在该范围内随机搜索的方法，贝叶斯超参数的方法还是差一些

评价

在实践的时候，有一个总是能提升神经网络几个百分点准确率的办法，就是在训练的时候训练几个独立的模型，然后在测试的时候平均它们预测结果。集成的模型数量增加，算法的结果也单调提升（但提升效果越来越少）。还有模型之间的差异度越大，提升效果可能越好。进行集成有以下几种方法：

同一个模型，不同的初始化。使用交叉验证来得到最好的超参数，然后用最好的参数来训练不同初始化条件的模型。这种方法的风险在于多样性只来自于不同的初始化条件
在交叉验证中发现最好的模型。使用交叉验证来得到最好的超参数，然后取其中最好的几个模型来进行集成。这样就提高了集成的多样性，但风险在于可能会包含不够理想的模型。在实际操作中，这样操作起来比较简单，在交叉验证后就不需要额外的训练了
一个模型设置多个记录点。如果训练非常耗时，那就在不同的训练时间对网络留下记录点（比如每个周期结束），然后用它们来进行模型集成。很显然，这样做多样性不足，但是在实践中效果还是不错的，这种方法的优势是代价比较小
在训练的时候跑参数的平均值。在训练过程中，如果损失值相较于前一次权重出现指数下降时，就在内存中对网络的权重进行一个备份。这样就可以对前几次循环中的网络状态进行平均了。会发现这个平滑过的版本的权重总是能得到更少的误差。直观的理解就是目标函数是一个碗状的，你的网络在这个周围跳跃，所以对它们平均一下，就更可能跳到中心去

用来构建卷积神经网络的各种层

与常规神经网络不同，卷积神经网络的各层中的神经元是 3 维排列的：宽度、高度和深度。（这里的深度指的是激活数据体的第三个维度，而不是整个网络的深度，整个网络的深度指的是网络的层数）

举个例子，CIFAR-10 中的图像是作为卷积神经网络的输入，该数据体的维度是 32 x 32 x 3 （宽度，高度和深度）。我们将看到，层中的神经元将只与前一层中的一小块区域连接，而不是采取全连接方式。对于用来分类 CIFAR-10 中的图像的卷积网络，其最后的输出层的维度是 1 x 1 x 10，因为在卷积神经网络结构的最后部分将会把全尺寸的图像压缩为包含分类评分的一个向量，向量是在深度方向排列的。下面是例子：

一个简单的卷积神经网络是由各种层按照顺序排列组成，网络中的每个层使用一个可以微分的函数将激活数据从一个层传递到另一个层。卷积神经网络主要由三种类型的层构成

卷积层
Pooling 层
全连接层

通过将这些层叠加起来，就可以构建一个完整的卷积神经网络

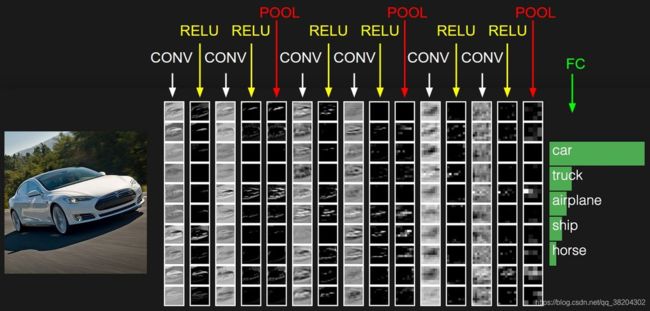
在上面的图片中，左边的输入层存有原始图像像素，右边的输出层存有类别分类评分。在处理流程中的每个激活数据体是铺成一列来展示的。因为对 3D 数据作图比较困难，我们就把每个数据体切成层，然后铺成一列显示。最后一层装的是针对不同类别的分类得分，这里只显示了得分最高的5个评分值和对应的类别

卷积层

卷积层的参数是由一些可学习的滤波器集合构成的。每个滤波器在空间上（宽度和高度）都比较小，但是深度和输入数据一致

举例来说，卷积神经网络第一层的一个典型的滤波器的尺寸可以是 5 x 5 x 3（宽高都是 5 像素，深度是 3，因为图像应为颜色通道，所以有 3 的深度）。在前向传播的时候，让每个滤波器都在输入数据的宽度和高度上滑动（更精确地说是卷积），然后计算整个滤波器和输入数据任一处的内积。当滤波器沿着输入数据的宽度和高度滑过后，会生成一个 2 维的激活图（activation map），激活图给出了在每个空间位置处滤波器的反应。直观地来说，网络会让滤波器学习到当它看到某些类型的视觉特征时就激活，具体的视觉特征可能是某些方位上的边界，或者在第一层上某些颜色的斑点，甚至可以是网络更高层上的蜂巢状或者车轮状图案

在每个卷积层上，我们会有一整个集合的滤波器（比如 12 个），每个都会生成一个不同的二维激活图。将这些激活映射在深度方向上层叠起来就生成了输出数据

在处理图像这样的高维度输入时，让每个神经元都与前一层中的所有神经元进行全连接是不现实的。相反，我们让每个神经元只与输入数据的一个局部区域连接。该连接的空间大小叫做神经元的 『感受野（receptive field）』，它的尺寸是一个超参数（其实就是滤波器的空间尺寸）。在深度方向上，这个连接的大小总是和输入量的深度相等。需要再次强调的是，我们对待空间维度（宽和高）与深度维度是不同的：连接在空间（宽高）上是局部的，但是在深度上总是和输入数据的深度一致

接着我们输出数据中神经元的数量，以及他们的排列方式，3 个超参数控制着输出数据体的尺寸：深度、步长和零填充

首先，输出数据体的深度是一个超参数：它和使用的滤波器的数量一致，而每个滤波器在输入数据中寻找一些不同的东西。举例来说，如果第一个卷积层的输入是原始图像，那么在深度维度上的不同神经元将可能被不同方向的边界，或者是颜色斑点激活。我们将这些沿着深度方向排列、感受野相同的神经元集合称为 『深度列（depth column）』
其次，在滑动滤波器的时候，必须指定步长。当步长为 1，滤波器每次移动 1 个像素。当步长为 2，滤波器滑动时每次移动 2 个像素。这个操作会让输出数据体在空间上变小
在下文可以看到，有时候将输入数据体用 0 在边缘处进行填充是很方便的。这个零填充的尺寸是一个超参数。零填充有一个良好性质——可以控制输出数据体的空间尺寸（最常用的是用来保持输入数据体在空间上的尺寸，这样输入和输出的宽高都相等）

输出数据体在空间上的尺寸可以通过输入数据体尺寸（ $W$ ），卷积层中神经元的感受野尺寸（ $F$ ），步长（ $S$ ）和零填充的数量（ $P$ ）的函数来计算。（注,这里假设输入数组的空间形状是正方形，即高度和宽度相等）输出数据体的空间尺寸为 $(W - F + 2 P) / S + 1$

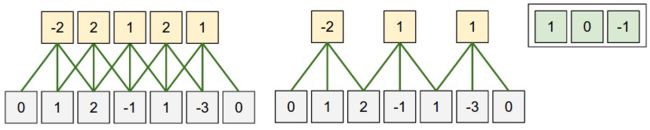
上图示例只有一个空间维度，神经元的感受野尺寸 F = 3，输入尺寸 W = 5，零填充 P = 1。左边：神经元使用的步长 S = 1，所以输出尺寸是 ( 5 - 3 + 2 ) / 1 + 1 = 5；右边：神经元的步长 S = 2，则输出尺寸是 ( 5 - 3 + 2) / 2 + 1 = 3。注意，当步长 S = 3 时是无法使用的，因为它无法整齐地穿过数据体。从等式上来说，因为 ( 5 - 3 + 2 ) = 4 是不能被 3 整除的

在上面左边例子中，注意输入维度是 5，输出维度也是 5。之所以如此，是因为感受野是 3 并且使用了 1 的零填充。如果不使用零填充，则输出数据体的空间维度就只有 3，因为这就是滤波器整齐滑过并覆盖原始数据需要的数目。一般说来，当步长 $S = 1$ 时，零填充的值是 $P = (F - 1) / 2$ ，这样就能保证输入和输出数据体有相同的空间尺寸。这样做非常常见，在介绍卷积神经网络的结构的时候我们会详细讨论其原因

在卷积层中使用参数共享来控制参数的数量。我们简单解释一下什么是参数共享：

如果一个特征在计算某个空间位置 $x_1,y_1)$ 的时候有用，那么它在计算另一个不同位置 $x_2,y_2)$ 的时候也有用。基于这个假设，可以显著地减少参数数量。换言之，就是将深度维度上一个单独的 2 维切片看做 『深度切片（depth slice）』，比如一个数据体尺寸为 [ 55 x 55 x 96 ] 的就有 96 个深度切片，每个尺寸为 [ 55 x 55 ]。在每个深度切片上的神经元都使用同样的权重和偏差。

先不考虑参数共享，我们以 AlexNet 为例，其输入图像的尺寸是 [ 227 x 227 x 3 ]。在第一个卷积层，神经元使用的感受野尺寸 F = 11，步长 S = 4，不使用零填充 P = 0。因为 ( 227 - 11 ) / 4 + 1 = 55，卷积层的深度 K = 96，则卷积层的输出数据体尺寸为 [ 55 x 55 x 96 ]。55 x 55 x 96 个神经元中，每个都和输入数据体中一个尺寸为 [ 11 x 11 x 3 ] 的区域全连接。在第一个卷积层就有 55 x 55 x 96 = 290,400 个神经元，每个有 11 x 11 x 3 = 364 个参数和 1 个偏差。将这些合起来就是 290400 x 364 = 105,705,600 个参数。单单第一层就有这么多参数，显然这个数目是非常大的

然而在参数共享下，例子中的第一个卷积层就只有 96 个不同的权重集了，一个权重集对应一个深度切片，共有 96 x 11 x 11 x 3 = 34,848 个不同的权重，或 34,944 个参数（+96 个偏差）。在每个深度切片中的 55 x 55 个权重使用的都是同样的参数。在反向传播的时候，都要计算每个神经元对它的权重的梯度，但是需要把同一个深度切片上的所有神经元对权重的梯度累加，这样就得到了对共享权重的梯度。这样，每个切片只更新一个权重集

【这句话啥意思】在反向传播的时候，都要计算每个神经元对它的权重的梯度，但是需要把同一个深度切片上的所有神经元对权重的梯度累加，这样就得到了对共享权重的梯度。这样，每个切片只更新一个权重集

参数共享的假设是有道理的：如果在图像某些地方探测到一个水平的边界是很重要的，那么在其他一些地方也会同样是有用的，这是因为图像结构具有平移不变性

注意，有时候参数共享假设可能没有意义，特别是当卷积神经网络的输入图像是一些明确的中心结构时候。这时候我们就应该期望在图片的不同位置学习到完全不同的特征。一个具体的例子就是输入图像是人脸，人脸一般都处于图片中心。你可能期望不同的特征，比如眼睛特征或者头发特征，它们会在图片的不同位置被学习。在这样的例子中，通常就放松参数共享的限制，将层称为 『局部连接层（Locally-Connected Layer）』

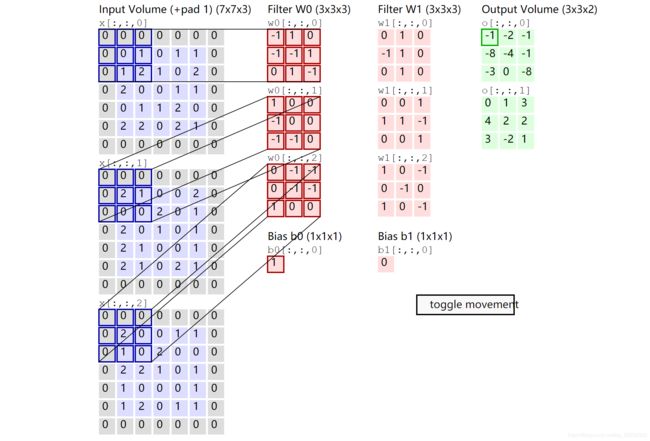
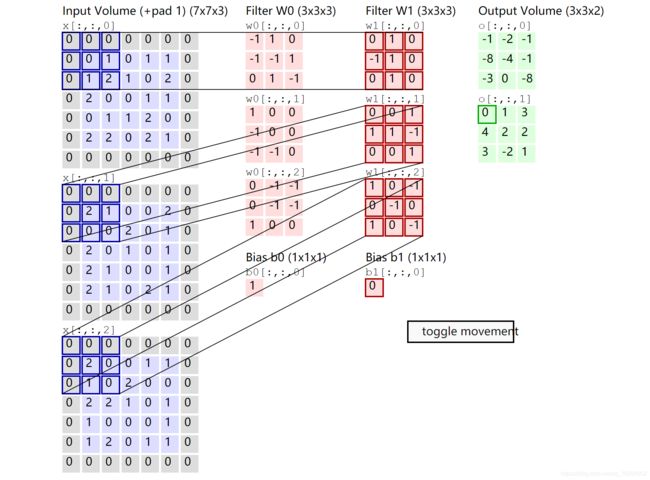
下面是一个卷积层的运行演示。因为 3D 数据难以可视化，所以所有的输入数据都采用将深度切片按照列的方式排列展示（输入数据体是蓝色，权重数据体是红色，输出数据体是绿色）。输入数据体的尺寸是 $W_1=5,H_1=5,D_1=3$ ，卷积层参数 $K = 2, F = 3, S = 2, P = 1$

也就是说，有 $2$ 个滤波器，滤波器的尺寸 $[3\times3]$ ，它们的步长是 $2$ .因此，输出数据体的空间尺寸是(5-3+2)/2+1=3。注意输入数据体使用了零填充 $P = 1$ ，所以输入数据体外边缘一圈都是 0

下面的例子在绿色的输出激活数据上循环演示，展示了其中每个元素都是先通过蓝色的输入数据和红色的滤波器逐元素相乘，然后求其总和，最后加上偏差得来

用矩阵乘法实现卷积：

输入图像的局部区域被 im2col 操作拉伸为列
比如，如果输入是 [ 227 x 227 x 3 ] ，要与尺寸为 11 x 11 x 3 的滤波器以步长为 4 进行卷积，就取输入中的 [ 11 x 11 x 3 ] 数据块，然后将其拉伸为长度为 11 x 11 x 3 = 363 的列向量。重复进行这一过程，因为步长为 4，所以输出的宽高为 ( 227 - 11 ) / 4 + 1 = 55，所以得到 im2col 操作的输出矩阵 X_col 的尺寸是 [ 363 x 3025 ]，其中每列是拉伸的感受野，共有 55 x 55 = 3,025 个。注意，因为感受野之间有重叠，所以输入数据体中的数字在不同的列中可能有重复
卷积层的权重也同样被拉伸成行。举例，如果有 96 个尺寸为 [ 11 x 11 x 3 ] 的滤波器，就生成一个矩阵 W_row，尺寸为 [ 96 x 363 ]
现在卷积的结果和进行一个大矩阵乘 np.dot(W_row, X_col) 是等价的了，能得到每个滤波器和每个感受野间的点积。在我们的例子中，这个操作的输出是 [ 96 x 3025 ]，给出了每个滤波器在每个位置的点积输出
结果最后必须被重新变为合理的输出尺寸 [ 55 x 55 x 96]

扩张卷积

最近一个研究给卷积层引入了一个新的叫 『扩张（dilation）』 的超参数。到目前为止，我们只讨论了卷积层滤波器是连续的情况。但是，让滤波器中元素之间有间隙也是可以的，这就叫做扩张。举例，在某个维度上滤波器 w 的尺寸是 3，那么计算输入 x 的方式是：w[0]*x[0] + w[1]*x[1] + w[2]*x[2]，此时扩张为 0。如果扩张为 1，那么计算为： w[0]*x[0] + w[1]*x[2] + w[2]*x[4]。换句话说，操作中存在 1 的间隙。在某些设置中，扩张卷积与正常卷积结合起来非常有用，因为这样做可以在很少的层数内更快地汇集输入图片的大尺度特征。比如，如果上下重叠 2 个 3 x 3 的卷积层，那么第二个卷积层的神经元的感受野是输入数据体中 5 x 5 的区域（可以理解成这些神经元的有效感受野是 5 x 5）。如果我们对卷积进行扩张，那么这个有效感受野就会迅速增长

汇聚层

通常，在连续的卷积层之间会周期性地插入一个汇聚层（Pooling 层）。它的作用是逐渐降低数据体的空间尺寸，这样的话就能减少网络中参数的数量，使得计算资源耗费变少，也能有效控制过拟合。汇聚层使用 MAX 操作，对输入数据体的每一个深度切片独立进行操作，改变它的空间尺寸。最常见的形式是汇聚层使用尺寸 2 x 2 的滤波器，以步长为 2 来对每个深度切片进行降采样，将其中 75% 的激活信息都丢掉。每个 MAX 操作是从 4 个数字中取最大值（也就是在深度切片中某个 2 x 2 的区域）。深度保持不变

下面是一些关于汇聚层的公式：

输入数据体尺寸 $W_1\cdot H_1\cdot D_1$
超参数，空间大小 $F$ ，步长 $S$
输出数据体尺寸 $W_2\cdot H_2\cdot D_2$

有如下的关系式， $W_2=(W_1-F)/S+1$ ， $H_2=(H_1-F)/S+1$ ， $D 2 = D 1$

注意两点，

因为对输入进行的是固定函数计算，所以汇聚层没有引入参数
在汇聚层中很少使用零填充

在实践中，最大汇聚层通常只有两种形式：一种是 $F = 3, S = 2$ ，也叫重叠汇聚（overlapping pooling），另一个更常用的 $F = 2, S = 2$ 。对更大感受野进行汇聚需要的汇聚尺寸也更大，但是这往往对网络是具有破坏性的

除了最大汇聚，汇聚单元还可以使用其他的函数，比如平均汇聚（average pooling）或 L2 范式汇聚（L2-norm pooling）。平均汇聚历史上比较常用，但是现在已经很少使用了。因为实践证明，最大汇聚的效果比平均汇聚要好

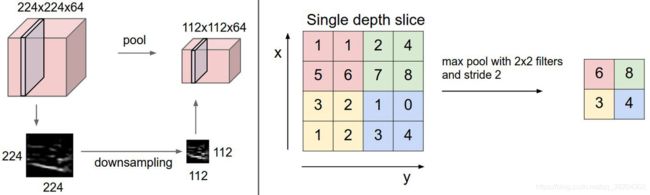
回顾一下反向传播的内容，其中 $m a x (x, y)$ 函数的反向传播可以简单理解为将梯度只沿最大的数回传。因此，在向前传播经过汇聚层的时候，通常会把池中最大元素的索引记录下来，这样在反向传播的时候梯度的路由就很高效

把全连接层化成卷积层

全连接层和卷积层之间唯一的不同就是卷积层中的神经元只与输入数据中的一个局部区域连接，并且在卷积列中的神经元共享参数。然而在两类层中，神经元都是计算点积，所以它们的函数形式是一样的。因此，将此两者相互转化是可能的：

对于任一个卷积层，都存在一个能实现和它一样前向传播的全连接层。权重矩阵是一个巨大的矩阵，除了某些特定块（这是因为有局部连接），其余部分都是零。而在其中大部分块中，元素都是相等的（因为参数共享）。
同样的，任何全连接层都可以被转化为卷积层。比如，一个 $K = 4096$ 的全连接层，输入数据体的尺寸是 $7\times7\times512$ ，这个全连接层可以被等效地看做一个 $F = 7, P = 0, S = 1, K = 4096$ 的卷积层。换句话说，就是将滤波器的尺寸设置为和输入数据体的尺寸一致了。因为只有一个单独的深度列覆盖并滑过输入数据体，所以输出将变成 $1\times1\times4096$ ，这个结果就和使用初始的那个全连接层一样了

在两种变换中，将全连接层转化为卷积层在实际运用中更加有用。假设一个卷积神经网络的输入是 224 x 224 x 3 的图像，一系列的卷积层和汇聚层将图像数据变为尺寸为 7 x 7 x 512 的激活数据体（在 AlexNet 中就是这样，通过使用 5 个汇聚层来对输入数据进行空间上的降采样，每次尺寸下降一半，所以最终空间尺寸为 224 / 2 / 2 / 2 / 2 / 2 = 7）。从这里可以看到，AlexNet 使用了两个尺寸为 4096 的全连接层，最后一个有 1000 个神经元的全连接层用于计算分类评分。我们可以将这 3 个全连接层中的任意一个转化为卷积层：

针对第一个连接区域是 [ 7 x 7 x 512 ] 的全连接层，令其滤波器尺寸为 $F = 1$ ，这样输出数据体就为 [ 1 x 1 x 4096 ] 了
针对第二个全连接层，令其滤波器尺寸为 $F = 1$ ，这样输出数据体为 [ 1 x 1 x 4096 ]
对最后一个全连接层也做类似的，令其 $F = 1$ ，最终输出为 [ 1 x 1 x 1000 ]

实际操作中，每次这样的变换都需要把全连接层的权重 $W$ 重塑成卷积层的滤波器。那么这样的转化有什么作用呢？

我们看这样一个例子，如果我们让 224 x 224 尺寸的浮窗，以步长为 32 在 384 x 384 的图片上滑动，把每个经停的位置都带入卷积网络，最后得到 6 x 6 个位置的类别得分。上述把全连接层转换成卷积层的做法会更简便。如果 224 x 224 的输入图片经过卷积层和汇聚层之后得到了 [ 7 x 7 x 512 ] 的数组，那么，384 x 384 的大图片直接经过同样的卷积层和汇聚层之后会得到 [ 12 x 12 x 512 ] 的数组（因为途径 5 个汇聚层，尺寸变为 384 / 2 / 2 / 2 / 2 / 2 = 12）。然后再经过上面由 3 个全连接层转化得到的 3 个卷积层，最终得到 [ 6 x 6 x 1000 ] 的输出（因为 ( 12 - 7 ) / 1 + 1 = 6）。这个结果正是浮窗在原图经停的 6 x 6 个位置的得分

相较于使用被转化前的原始卷积神经网络对所有 36 个位置进行迭代计算，使用转化后的卷积神经网络进行一次前向传播计算要高效得多，因为 36 次计算都在共享计算资源。这一技巧在实践中经常使用，用于一次获得较好的结果。比如，通常将一张图像尺寸变得更大，然后使用变换后的卷积神经网络来对空间上很多不同位置进行评价得到分类评分，然后在求这些分值的平均值

最后，如果我们想用步长小于 32 的浮窗怎么办？用多次的向前传播就可以解决。比如我们想用步长为 16 的浮窗。那么可以先使用原图在转化后的卷积网络执行向前传播，然后分别沿宽度，沿高度，最后同时沿宽度和高度，把原始图片分别平移 16 个像素，然后把这些平移之后的图分别带入卷积网络

卷积神经网络

层的排列规律

卷积神经网络最常见的形式就是将一些卷积层和 ReLU 层放在一起，其后紧跟汇聚层，然后重复如此直到图像在空间上被缩小到一个足够小的尺寸，在某个地方过渡成全连接层也较为常见。最后的全连接层得到输出，比如分类评分等。换句话说，最常见的卷积神经网络结构如下：

INPUT → [[CONV → RELU]*N → POOL?]*M → [FC → RELU]*K → FC

下面是一些常见的网络结构规律：

INPUT → FC，实现一个线性分类器，此处 N = M = K = 0
INPUT → CONV → RELU → FC
INPUT → [CONV → RELU → POOL]*2 → FC → RELU → FC，此处在每个汇聚层之间有一个卷积层
INPUT → [CONV → RELU → CONV → RELU → POOL]*3 → [FC → RELU]*2 → FC，此处每个汇聚层前有两个卷积层，这个思路适用于更大更深的网络，因为在执行具有破坏性的汇聚操作前，多重的卷积层可以从输入数据中学习到更多的复杂特征

几个小滤波器卷积层的组合比一个大滤波器卷积层好：假设你一层一层地重叠了 3 个 3 x 3 的卷积层（层与层之间有非线性激活函数）。在这个排列下，第一个卷积层中的每个神经元都对输入数据体有一个 3 x 3 的视野。第二个卷积层上的神经元对第一个卷积层有一个 3 x 3 的视野，也就是对输入数据体有 5 x 5 的视野。同样，在第三个卷积层上的神经元对第二个卷积层有 3 x 3 的视野，也就是对输入数据体有 7 x 7 的视野。假设不采用这 3 个 3 x 3 的卷积层，而是使用一个单独的 7 x 7 感受野的卷积层，那么所有神经元的感受野也是 7 x 7，这有一些缺点

下面我们提几点小滤波器组合比大滤波器好的原因，

首先，多个卷积层与非线性的激活层交替的结构，比单一卷积层的结构更能提取出深层的更好的特征
其次，假设所有的数据有 $C$ 个通道，那么单独的 7 x 7 卷积层将会包含 $C\times(7\times7\times C)=49C^2$ 个参数，而 3 个 3 x 3 的卷积层的组合仅有 $3\times(C\times(3\times3\times C))= 27C^2$ 个参数

因此，直观说来，最好选择带有小滤波器的卷积层组合，而不是用一个带有大的滤波器的卷积层。小滤波器组合可以表达出输入数据中更多个强力特征，使用的参数也更少。唯一的不足是，在进行反向传播时，中间的卷积层可能会导致占用更多的内存

层的尺寸设置规律

现在先介绍设置结构尺寸的一般性规则，然后根据这些规则进行讨论：

输入层（包含图像的）应该能被 2 整除很多次。常用数字包括 32（比如CIFAR-10）、64、96（比如STL-10）或 224（比如 ImageNet 卷积神经网络）、384 和 512

卷积层应该使用小尺寸滤波器（比如 3 x 3 或最多 5 x 5），使用步长 $S = 1$ 。还有一点非常重要，就是对输入数据进行零填充，这样卷积层就不会改变输入数据在空间维度上的尺寸。比如，当 $F = 3$ ，那就使用 $P = 1$ 来保持输入尺寸。一般对于任意 $F$ ，当 $P = (F - 1) / 2$ 的时候就能保持输入尺寸。如果必须使用更大的滤波器尺寸（比如 7 x 7 之类），通常只用在第一个面对原始图像的卷积层上

汇聚层负责对输入数据的空间维度进行降采样。最常用的设置是用 2 x 2 感受野（即 $F = 2$ ）的 max pooling，步长为2（即 $S = 2$ ）。注意这一操作将会把输入数据中 75% 的激活数据丢弃（因为对宽度和高度都进行了 2 的降采样）。另一个不那么常用的设置是使用 3 x 3 的感受野，步长为 2。max pooling 的感受野尺寸很少有超过 3 的，因为汇聚操作过于激烈，易造成数据信息丢失，这通常会导致算法性能变差

减少尺寸设置的问题：上文中展示的设置是很好的，因为所有的卷积层都能保持其输入数据的空间尺寸，汇聚层只负责对数据体从空间维度进行降采样。如果使用的步长大于 1 并且不对卷积层的输入数据使用零填充，那么就必须非常仔细地监督输入数据体通过整个卷积神经网络结构的过程，确认所有的步长和滤波器都尺寸互相吻合

为什么在卷积层使用 1 的步长？ 在实际应用中，更小的步长效果更好。上文也已经提过，步长为 1 可以让降采样的任务全部由汇聚层负责，卷积层只负责对输入数据体的深度进行变换

为何使用零填充？ 使用零填充除了前面提到的可以让卷积层的输出数据保持和输入数据在空间维度的不变，还可以提高算法性能。如果卷积层值进行卷积而不进行零填充，那么数据体的尺寸就会略微减小，那么图像边缘的信息就会过快地损失掉

因为内存限制所做的妥协：在某些案例（尤其是早期的卷积神经网络结构）中，基于前面的各种规则，内存的使用量迅速飙升。例如，使用 64 个尺寸为 3 x 3 的滤波器对 224 x 224 x 3 的图像进行卷积，零填充为 1，得到的激活数据体尺寸是 [ 224 x 224 x 64 ]，这个数量就是一千万的激活数据，或者等同于 72MB 的内存。因为 GPU 通常因为内存导致性能瓶颈，所以做出一些妥协是必须的。在实践中，人们倾向于在网络的第一个卷积层做出妥协。例如，可能在第一个卷积层使用步长 2，尺寸 7 x 7 的滤波器。实际中也是这样，在 AlexNet 中，第一层滤波器的尺寸为 11 x 11，步长为 4