通过VGG16理解池化、卷积、激活函数

理论理解：

1、卷积池化？

 

图中卷积核为：

计算公式为：

1*1+1*0+1*1+0*0+1*1+1*0+0*1+0*0+1*1=4

以此类推...

4、3、4

2、4、3

2、3、4

卷积层关键操作：

局部关联：每个神经元看作一个滤波器filter，局部数据权值共享。
滑动窗口：对一个filter内的数据进行计算。

关键参数：

深度depth：filter的个数
步长stride：单个filter一次滑动的长度
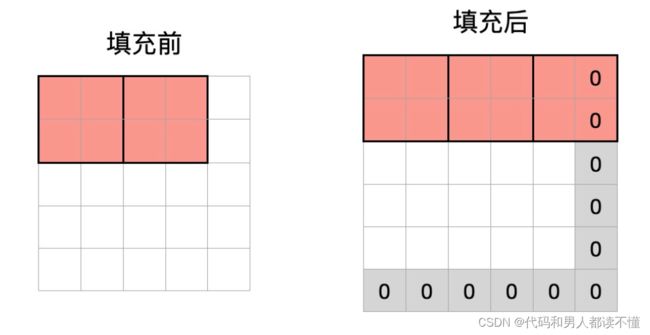
填充值zero-padding：对输入数据进行填充

填充值的作用：对于一个像素为5x5的输入图片，如果滑动窗口的大小为2x2，步长为2，则存在一列数据无法处理，此时需要添加0填充值，以保证所有数据都能被遍历到。

padding填充值的相应理解：

PyTorch中的padding（边缘填充）操作_hyk_1996的博客-CSDN博客_padding_mode

Pytorch 四种边界填充方式(Padding) - 抚琴尘世客 - 博客园 (cnblogs.com)

maxpool(最大池化)：最大池化就是取filter对应区域内最大像素值替代该像素点值，其作用是降维。在这里，池化使用的滤波器都是2*2大小，因此池化后得到的图像大小为原来的1/2。下图为最大池化过程：

 卷积的计算公式：

若图像为正方形：设图像尺寸为W×W，卷积核尺寸为F×F，步长为S，Padding为P，经过卷积层后输出的图片为N×N：

若图像为矩形：设输入图像尺寸为W×H，卷积核的尺寸为F×F，步长为S，图像的深度为C，Padding为P，则卷积后输出图像大小：

输出图像的通道数为C

池化的计算公式：

设输入图像尺寸为W×H，其中W：图像宽，H：图像高，D：图像深度（通道数），卷积核的尺寸为F×F，S为步长，池化后输出图像大小：

---

参考链接：卷积神经网络——卷积层计算_HelloWorldQAQ。的博客-CSDN博客_卷积层计算

【深度学习】全面理解VGG16模型_Florrie Zhu的博客-CSDN博客_vgg16模型的作用

2、激活函数？

激活函数的作用：激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。

常见的激活函数：

Sigmoid函数

特点：

        它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.

缺点:

        缺点1：在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大

        缺点2：Sigmoid 的 output 不是0均值（即zero-centered）。这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。 产生的一个结果就是：如x>0, x>0, f= ,那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。 当然了，如果按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的梯度消失问题相比还是要好很多的。

        缺点3：其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。

tanh函数

 

 

特点:

1.tahn解决了Sigmoid函数的不是zero-centered输出问题，

2.然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

ReLU函数

 

 

ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient

有以下几大优点：

        1） 解决了gradient vanishing问题 (在正区间)

        2）计算速度非常快，只需要判断输入是否大于0

        3）收敛速度远快于sigmoid和tanh

ReLU问题：

        1）ReLU的输出不是zero-centered

        2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生:

                (1) 非常不幸的参数初始化，这种情况比较少见

                (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

---

 参考链接：为什么要使用激活函数,激活函数的作用_贾世林jiashilin的博客-CSDN博客_为什么要用激活函数

VGG：

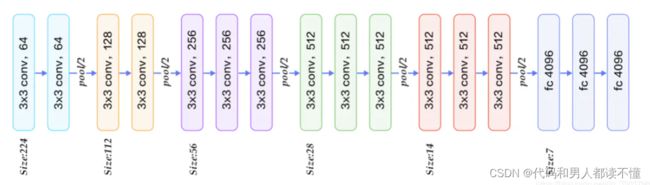
 1、网络结构

        vgg16总共有16层，13个卷积层和3个全连接层，第一次经过64个卷积核的两次卷积后，采用一次pooling，第二次经过两次128个卷积核卷积后，再采用pooling，再重复两次三个512个卷积核卷积后，再pooling，最后经过三次全连接。

2、VGG16的卷积核

        conv3-xxx：卷积层全部都是3*3的卷积核，用上图中conv3-xxx表示，xxx表示通道数。其步长为1，用padding=same填充。池化层的池化核为2*2
input（224x224 RGB image） ：指的是输入图片大小为224*244的彩色图像，通道为3，即224*224*3；
        maxpool ：是指最大池化，在vgg16中，pooling采用的是2*2的最大池化方法；
FC-4096 :指的是全连接层中有4096个节点，同样地，FC-1000为该层全连接层有1000个节点；
        padding：指的是对矩阵在外边填充n圈，padding=1即填充1圈，5X5大小的矩阵，填充一圈后变成7X7大小；
        最后补充，vgg16每层卷积的滑动步长stride=1，padding=1，卷积核大小为333；

3. 卷积计算 

        1）输入图像尺寸为224x224x3，经64个通道为3的3x3的卷积核，步长为1，padding=same填充，卷积两次，再经ReLU激活，输出的尺寸大小为224x224x64 

（padding = same：填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致。通过卷积的计算公式可以知道padding       P = 112）

        2）经max pooling（最大化池化），滤波器为2x2，步长为2，图像尺寸减半，池化后的尺寸变为112x112x64 
        3）经128个3x3的卷积核，两次卷积，ReLU激活，尺寸变为112x112x128 
        4）max pooling池化，尺寸变为56x56x128 
        5）经256个3x3的卷积核，三次卷积，ReLU激活，尺寸变为56x56x256 
        6）max pooling池化，尺寸变为28x28x256 
        7）经512个3x3的卷积核，三次卷积，ReLU激活，尺寸变为28x28x512 
        8）max pooling池化，尺寸变为14x14x512 
        9）经512个3x3的卷积核，三次卷积，ReLU激活，尺寸变为14x14x512 
        10）max pooling池化，尺寸变为7x7x512 
        11）然后Flatten()，将数据拉平成向量，变成一维51277=25088。 
        12）再经过两层1x1x4096，一层1x1x1000的全连接层（共三层），经ReLU激活 
        13）最后通过softmax输出1000个预测结果

softmax的解释：

Softmax与交叉熵损失的实现及求导 - 知乎 (zhihu.com)

---

参考链接：深度学习-VGG16原理详解_é£的博客-CSDN博客_vgg16