吴恩达机器学习系列课程笔记——第三章:线性代数回顾(Linear Algebra Review)
3.1 矩阵和向量
https://www.bilibili.com/video/BV164411b7dx?p=12
矩阵的维数即行数×列数
矩阵元素(矩阵项):
Aij指第i行,第j列的元素。
向量是一种特殊的矩阵,讲义中的向量一般都是列向量,如
如下图为1索引向量和0索引向量,左图为1索引向量,右图为0索引向量,一般我们用1索引向量。
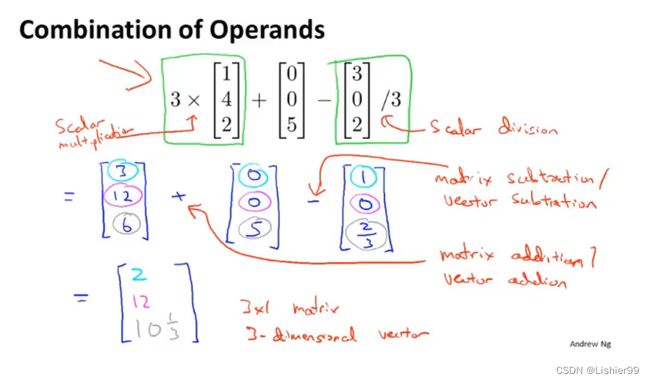
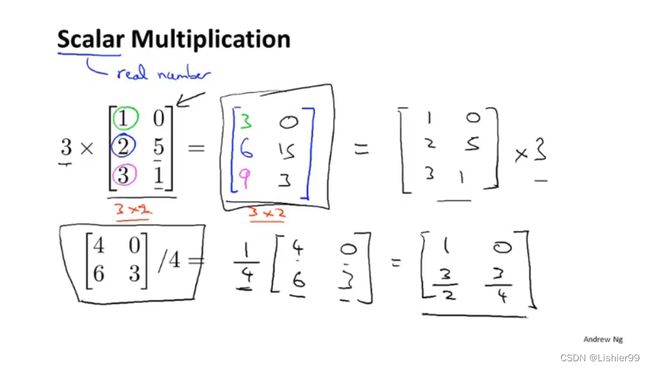
3.2 加法和标量乘法
https://www.bilibili.com/video/BV164411b7dx?p=13
矩阵的加法:行列数相等的可以加。
矩阵的乘法:每个元素都要乘。
组合算法也类似。
3.3 矩阵向量乘法
https://www.bilibili.com/video/BV164411b7dx?p=14
矩阵和向量的乘法如图:m×n的矩阵乘以n×1的向量,得到的是m×1的向量,具体算法
实际运用例子:
当我们有预测算法h(x)时,并且数据集有4项,想要把所有数据进行预测得到结果
方式1:通过矩阵进行全部数据的预测
方法2:通过循环,对每个数据进行预测
对比:实际上,以后我们会面临很大的数据集,那么如果循环的话,可能会出现代码太长等问题,而用矩阵,我们就能够简化代码,只用一句代码就能解决问题,而且今后我们也会从另一个角度解释,为什么左边的方式更好。
3.4 矩阵乘法
https://www.bilibili.com/video/BV164411b7dx?p=15
维度必须匹配
将B看做几组列向量,每组列向量与A进行矩阵相乘,都得到C的一组列向量
实际案例:当我们不仅有多个数据集的的时候,而且还有多套预测函数时,可以用这种思路去编写代码
如蓝色、橙色、粉色各是预测函数对多组数据进行预测。而且为了实现矩阵间的乘法,有很多很好的线性代数库,这些库经过了高度优化,可以高效的实现矩阵间的乘法,帮助你进行矩阵运算。例如电脑的并行运算(SIMD)
3.5 矩阵乘法的性质
https://www.bilibili.com/video/BV164411b7dx?p=16
矩阵乘法的性质:
矩阵的乘法不满足交换律(绝大所数不满足,除非A是1行乘1列的矩阵或单位矩阵):
A×B≠B×A
矩阵的乘法满足结合律。即:
A×(B×C)=(A×B)×C
单位矩阵:在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,我们称这种矩阵为单位矩阵.它是个方阵,一般用 I 或者 E 表示,本讲义都用 I 代表单位矩阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1以外全都为0。如:
A × A逆=A逆 × A=I(单位矩阵)
对于单位矩阵,有
A × I = I × A
3.6 逆、转置
https://www.bilibili.com/video/BV164411b7dx?p=17
矩阵的逆:如矩阵A是一个m×m矩阵(方阵),如果有逆矩阵,则:
A × A逆=A逆 × A=I(单位矩阵)
矩阵的转置:设A为m×n阶矩阵(即m行n列),第i行j列的元素是a(i,j),即:A=a(i,j)
定义A的转置为这样一个n×m阶矩阵B,满足B=a(j,i),即 b(i,j)=a(j,i)(B的第i行第j列元素是A的第j行第i列元素),记AT=B。(有些书记为A’=B)
直观来看,将A的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转,即得到A的转置。
矩阵的转置基本性质:
(A×B)T=BT×AT
(AT)T=A
(KA)T=KAT






![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vMg1scjm-1657956450504)(C:\Users\admin\AppData\Roaming\Typora\typora-user-images\image-20220714154426165.png)]](http://img.e-com-net.com/image/info8/e3fc73ba3b7f4376ba392a4c585ae425.jpg)




