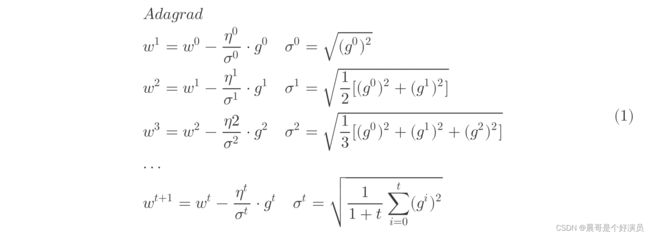误差和梯度下降

Datawhale开源学习，机器学习课程，项目地址：https://github.com/datawhalechina/leeml-notes

之前讲了线性模型，提到了误差，那么误差来自哪里？本节内容将介绍「偏差」、「方差」对模型拟合度的影响，同时介绍一下交叉验证、梯度下降法。

Estimator

$y$表示那个真正的function，而$f^{\ast }$表示这个$f$的估测值estimator，就好像在打靶，$f$是靶的中心点，收集到一些data做training以后，你会得到一个你觉得最好的function即$f^{\ast }$，这个$f^{\ast }$落在靶上的某个位置，它跟靶中心有一段距离，这段距离就是由bias和variance决定的。

实际上对应着物理实验中「系统误差」和「随机误差」的概念，假设有n组数据，每一组数据都会产生一个相应的$f^{\ast }$，此时bias表示所有$f^{\ast }$的平均落靶位置和真值靶心的距离，variance表示这些$f^{\ast }$的集中程度

Bias and Variance of Estimator

假设独立变量为$x$(这里的$x$代表每次独立地从不同的training data里训练找到的$f^{\ast }$)，那么，总体期望$E(x)=u$ ；总体方差$Var(x)={\sigma }^2$

用样本均值$\overline{x}$估测总体期望$u$

由于我们只有有限组样本 $\{x^1,x^2,...,x^N\}$，故样本均值$\overline{x}=\frac{1}{N}\sum _{i=1}^N{x}^i\ne \mu$ ；样本均值的期望$E(\overline{x})=E(\frac{1}{N}\sum _{i=1}^N{x}^i)=\mu$ ; 样本均值的方差$Var(\overline{x})=\frac{{\sigma }^2}{N}$。样本均值 $\overline{x}$的期望是总体期望$\mu$，也就是说$\overline{x}$是按概率对称地分布在总体期望$\mu$的两侧的；而$\overline{x}$分布的密集程度取决于N，即数据量的大小，如果N比较大，$\overline{x}$就会比较集中，如果N比较小，$\overline{x}$就会以$\mu$为中心分散开来（也就是说，对期望而言，期望值$\mu$为图像的对称轴，期望值$\mu$越大，越偏离对称轴$x=0$；同时对方差而言，N越大，方差越小，图像越「高瘦」；N越小，方差越大，图像越「矮胖」，所以方差反应的是数据的集中或离散程度）

综上，样本均值$\overline{x}$以总体期望$\mu$为中心对称分布，可以用来估测总体期望$\mu$。

用样本方差$s^2$估测总体方差${\sigma }^2$

由于我们只有有限组样本 $\{x^1,x^2,...,x^N\}$，故样本均值$\overline{x}=\frac{1}{N}\sum _{i=1}^N{x}^i$ ；样本方差$s^2=\frac{1}{N-1}\sum _{i=1}^N(x^i-\overline{x}{)}^2$ ；样本方差的期望$E(s^2)=\frac{N-1}{N}{\sigma }^2\ne {\sigma }^2$ ，同理，样本方差$s^2$以总体方差${\sigma }^2$为中心对称分布，可以用来估测总体方差${\sigma }^2$，而$s^2$分布的密集程度也取决于$N$。

现在我们要估测的是靶的中心$f$，每次collect data训练出来的$f^{\ast }$是打在靶上的某个点；产生的error取决于：

• 多次实验得到的$f^{\ast }$的期望$\overline{f}$与靶心$f$之间的bias——$E(f^{\ast })$，可以形象地理解为瞄准的位置和靶心的距离的偏差
• 多次实验的$f^{\ast }$之间的variance——$Var(f^{\ast })$，可以形象地理解为多次打在靶上的点的集中程度

误差

方差

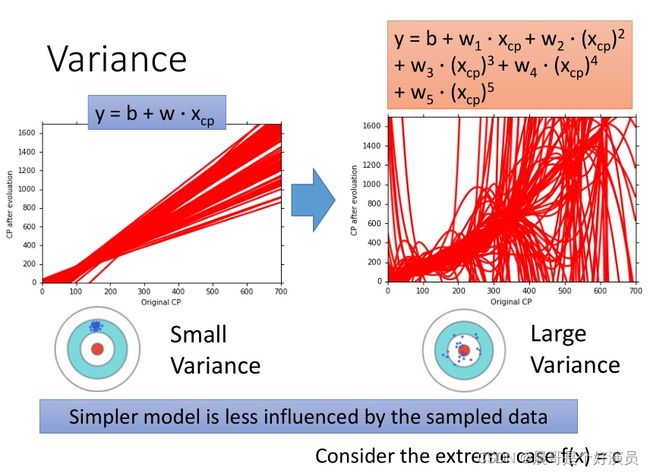
$f^{\ast }$的variance是由model决定的，一个简单的model在不同的training data下可以获得比较稳定分布的$f^{\ast }$，而复杂的model在不同的training data下的分布比较杂乱（如果data足够多，那复杂的model也可以得到比较稳定的分布）

如果采用比较简单的model，那么每次在不同data下的实验所得到的不同的$f^{\ast }$之间的variance是比较小的，就好像说，你在射击的时候，每次击中的位置是差不多的，就如同下图中的linear model，100次实验找出来的$f^{\ast }$都是差不多的。但是如果model比较复杂，那么每次在不同data下的实验所得到的不同的$f^{\ast }$之间的variance是比较大的，它的散布就会比较开，就如同图中含有高次项的model，每一条$f^{\ast }$都长得不太像，并且散布得很开。

QUESTION: 那为什么比较复杂的model，它的散布就比较开呢？比较简单的model，它的散布就比较密集呢？

原因其实很简单，其实前面在讲regularization正则化时也提到了部分原因。简单的model实际上就是没有高次项的model，或者高次项的系数非常小的model，这样的model表现得相当平滑，受到不同的data的影响是比较小的。举一个很极端的例子，我们的整个model(function set)里面，只有一个function: f=c，这个function只有一个常数项，因此无论training data怎么变化，从这个最简单的model里找出来的$f^{\ast }$都是一样的，它的variance就是等于0

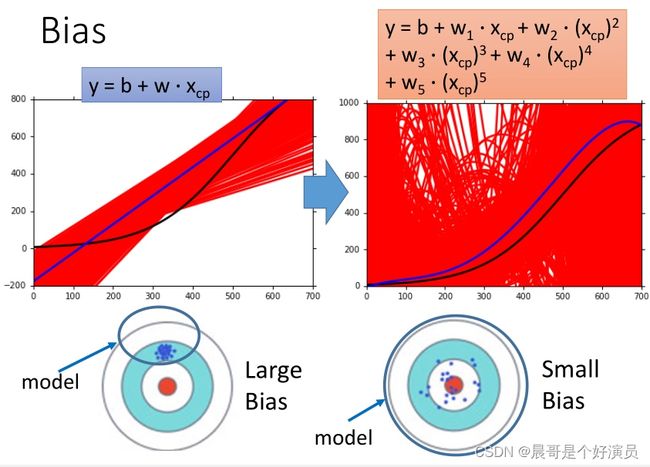
偏差

偏差bias的意思是，我们把所有的$f^{\ast }$平均起来得到$E(f^{\ast })=\overline{f^{\ast }}$，这个$\overline{f^{\ast }}$与真值$f$有多接近。当然这里会有一个问题，总体的真值$f$我们根本就没有办法知道，因此这里只是假定了一个$f$。当model比较简单的时候，每次实验得到的$f^{\ast }$之间的variance会比较小，这些$f^{\ast }$会稳定在一个范围内，但是它们的平均值$\overline{f}$距离真实值$f$会有比较大的偏差；而当model比较复杂的时候，每次实验得到的$f^{\ast }$之间的variance会比较大，实际体现出来就是每次重新实验得到的$f^{\ast }$都会与之前得到的有较大差距，但是这些差距较大的$f^{\ast }$的平均值$\overline{f}$却和真实值$f$比较接近。

也就是说，复杂的model，单次实验的结果是没有太大参考价值的，但是如果把考虑多次实验的结果的平均值，也许会对最终的结果有帮助。这里的单次实验指的是，用一组training data训练出model的一组有效参数以构成$f^{\ast }$(每次独立实验使用的training data都是不同的)

因此得出结论：

• 如果是一个比较简单的model，那它有比较小的variance和比较大的bias。每次实验的$f^{\ast }$都比较集中，但是他们平均起来距离靶心会有一段距离（比较适合实验次数少甚至只有单次实验的情况）
• 如果是一个比较复杂的model，每次实验找出来的$f^{\ast }$都不一样，它有比较大的variance但是却有比较小的bias。每次实验的$f^{\ast }$都比较分散，但是他们平均起来的位置与靶心比较接近（比较适合多次实验的情况）

Why？

实际上我们的model就是一个function set，当你定好一个model的时候，实际上就已经定好这个function set的范围了，那个最好的function只能从这个function set里面挑出来

如果是一个简单的model，它的function set的space是比较小的，这个范围可能根本就没有包含你的target；如果这个function set没有包含target，那么不管怎么sample，平均起来永远不可能是target

如果这个model比较复杂，那么这个model所代表的function set的space是比较大的，那它就很有可能包含target，只是它没有办法找到那个target在哪，因为你给的training data不够，你给的training data每一次都不一样，所以它每一次找出来的$f^{\ast }$都不一样，但是如果他们是散布在这个target附近的，那平均起来，实际上就可以得到和target比较接近的位置

偏差 vs 方差

由前面的讨论可知，比较简单的model，variance比较小，bias比较大；而比较复杂的model，bias比较小，variance比较大。

$${\text{error}}_{observed}={\text{error}}_{variance}+{\text{error}}_{bias}$$

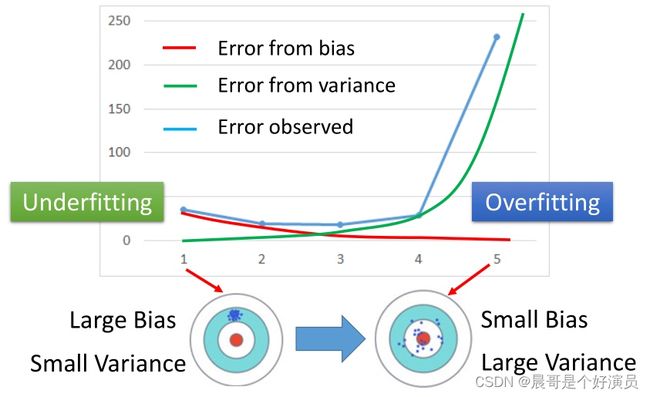
可以发现，随着model的逐渐复杂：

• bias逐渐减小，bias所造成的error也逐渐下降，也就是打靶的时候瞄得越来越准
• variance逐渐变大，variance所造成的error也逐渐增大，也就是虽然瞄得越来越准，但是每次射出去以后，你的误差是越来越大的
• 当bias和variance这两项同时被考虑的时候，也就是实际体现出来的error的变化
• 实际观测到的error先是减小然后又增大，因此实际error为最小值的那个点，即为bias和variance的error之和最小的点，就是表现最好的model
• 如果实际error主要来自于variance很大，这个状况就是overfitting过拟合；如果实际error主要来自于bias很大，这个状况就是underfitting欠拟合。

这就是我们之前要先计算出每一个model对应的error，再挑选error最小的model的原因，只有这样才能综合考虑bias和variance的影响，找到一个实际error最小的model。

误差来自于哪里？

当你自己在做research的时候，你必须要搞清楚，手头上的这个model，它目前主要的error是来源于哪里；你觉得你现在的问题是bias大，还是variance大，你应该先知道这件事情，你才能知道你的future work，你要improve你的model的时候，你应该要走哪一个方向

• 如果model没有办法fit training data的examples，代表bias比较大，这时是underfitting。形象地说，就是该model找到的$f^{\ast }$上面并没有training data的大部分样本点，代表说这个model跟正确的model是有一段差距的，所以这个时候是bias大的情况，是underfitting

• 如果model可以fit training data，在training data上得到小的error，但是在testing data上，却得到一个大的error，代表variance比较大，这时是overfitting

遇到bias大或variance大的时候，你其实是要用不同的方式来处理它们。

如果偏差过大，该怎么做？

bias大，代表你现在这个model里面可能根本没有包含你的target，$f$可能根本就不在你的function set里。对于error主要来自于bias的情况，是由于该model（function set）本来就不好，collect更多的data是没有用的，必须要从model本身出发redesign，重新设计你的model

For bias, redesign your model

• Add more features as input。比如pokemon的例子里，只考虑进化前cp值可能不够，还要考虑hp值、species种类…作为model新的input变量

如果方差过大，该怎么做？

• More data
  • Very effective, but not always practical
  • 如果是5次式，找100个$f^{\ast }$，每次实验我们只用10只宝可梦的数据训练model，那我们找出来的100个$f^{\ast }$的散布就会杂乱无章；但如果每次实验我们用100只宝可梦的数据训练model，那我们找出来的100个$f^{\ast }$的分布就非常地集中
  • 增加data是一个很有效控制variance的方法，假设你variance太大的话，collect data几乎是一个万能的东西，并且它不会伤害你的bias。但是它存在一个很大的问题是，实际上并没有办法去collect更多的data
  • 如果没有办法collect更多的data，其实有一招，根据你对这个问题的理解，自己去generate更多「假的」data
    • 比如手写数字识别，因为每个人手写数字的角度都不一样，那就把所有training data里面的数字都左转15°，右转15°
    • 比如做火车的影像辨识，只有从左边开过来的火车影像资料，没有从右边开过来的火车影像资料，实际上可以把每张图片都左右颠倒，就generate出右边的火车数据了，这样就多了一倍data出来
    • 比如做语音辨识的时候，只有男生说的“你好”，没有女生说的“你好”，那就用男生的声音用一个变声器把它转化一下，这样男女生的声音就可以互相转化，这样data就多了
    • 比如现在你只有录音室里录下的声音，但是detection实际要在真实场景下使用的，那你就去真实场景下录一些噪音加到原本的声音里，就可以generate出符合条件的data
• Regularization正则化
  • 在loss function里面再加一个与model高次项系数相关的term，它会希望你的model里高次项的参数越小越好，也就是说希望你今天找出来的曲线越平滑越好；这个新加的term前面可以有一个weight，代表你希望你的曲线有多平滑
  • 加了regularization后，一些怪怪的、很不平滑的曲线就不会再出现，所有曲线都集中在比较平滑的区域；增加weight可以让曲线变得更平滑
  • 加了regularization以后，因为你强迫所有的曲线都要比较平滑，所以这个时候也会让你的variance变小。但regularization是可能会伤害bias的，因为它实际上调整了function set的space范围，变成它只包含那些比较平滑的曲线，这个缩小的space可能没有包含原先在更大space内的$f$，因此伤害了bias，所以当你做regularization的时候，需要调整regularization的weight，在variance和bias之间取得平衡

模型选择

我们现在会遇到的问题往往是这样：我们有很多个model可以选择，还有很多参数可以调，比如regularization的weight，那通常我们是在bias和variance之间做一些trade-off。我们希望找一个model，它variance够小，bias也够小，这两个合起来给我们最小的testing data的error。

交叉验证

你要做的事情是，把你的training set分成两组：

• 一组是真正拿来training model的，叫做training set(训练集)
• 另外一组不拿它来training model，而是拿它来选model，叫做validation set(验证集)

先在training set上找出每个model最好的function $f^{\ast }$，然后用validation set来选择你的model，也就是说，你手头上有3个model，你先把这3个model用training set训练出三个$f^{\ast }$，接下来看一下它们在validation set上的performance。假设现在model 3的performance最好，那你可以直接把这个model 3的结果拿来apply在testing data上。如果你担心现在把training set分成training和validation两部分，感觉training data变少的话，可以这样做：已经从validation决定model 3是最好的model，那就定住model 3不变（function的表达式不变），然后使用全部的data去更新model 3表达式的参数。

这个时候，如果你把这个训练好的model的$f^{\ast }$apply到public testing set上面，虽然这么做，你得到的error表面上看起来是比较大的，但是这个时候你在public set上的error才能够真正反映你在private set上的error。当你得到public set上的error的时候（尽管它可能会很大），不建议回过头去重新调整model的参数，因为当你再回去重新调整什么东西的时候，你就又会把public testing set的bias给考虑进去了，这就又回到围绕着有偏差的testing data做model的优化。这样的话此时你在public set上看到的performance就没有办法反映实际在private set上的performance了。因为你的model是针对public set做过优化的，虽然public set上的error数据看起来可能会更好看，但是针对实际未知的private set，这个“优化”带来的可能是反作用，反而会使实际的error变大。

因此这里只是说，你要keep in mind，benchmark corpus上面所看到的testing的performance，说不定是别人特意调整过的，并且testing set与实际的数据也会有偏差，它的error，肯定是大于它在real application上应该有的值。比如说你现在常常会听到说，在image lab的那个corpus上面，error rate都降到3%，已经超越人类了。但是真的是这样子吗？如果已经用testing data调过参数了，你把那些model真的apply到现实生活中，它的error rate肯定是大于3%的。

N-fold交叉验证

如果你不相信某一次分train和validation的结果的话，那你就分很多种不同的样子。比如说，如果你做3-fold的validation，把training set分成三份，你每一次拿其中一份当做validation set，另外两份当training；分别在每个情境下都计算一下3个model的error，然后计算一下它的average error；然后你会发现在这三个情境下的average error，是model 1最好。然后接下来，你就把用整个完整的training data重新训练一遍model 1的参数；然后再去testing data上test。原则上是，如果你少去根据public testing set上的error调整model的话，那你在private testing set上面得到的error往往是比较接近public testing set上的error的

---

之前的文章有讨论过，拟合过程中的不断迭代参数权重的过程，使用的方法是梯度下降法，接下来详细介绍下什么是梯度下降法，以及常见的几种梯度下降法。

梯度下降

$${\theta }^{\ast }=\arg \underset{\theta }{\min }L(\theta )$$

$L$ : loss function

$\theta :$ parameters（「上标」表示第几组参数，「下标」表示这组参数中的第几个参数）

Suppose that $\theta$ has two variables $\left\{{\theta }_1,{\theta }_2\right\}$

Randomly start at ${\theta }^0=\left[\begin{array}{l}{\theta }_1^0\\ {\theta }_2^0\end{array}\right]$

计算$\theta$处的梯度：$\nabla L(\theta )=\left[\begin{array}{l}\partial L\left({\theta }_1\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2\right)/\partial {\theta }_2\end{array}\right]$

$$\begin{gathered} \left[\begin{array}{l}{\theta }_1^1\\ {\theta }_2^1\end{array}\right]=\left[\begin{array}{l}{\theta }_1^0\\ {\theta }_2^0\end{array}\right]-\eta \left[\begin{array}{l}\partial L\left({\theta }_1^0\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2^0\right)/\partial {\theta }_2\end{array}\right]\Rightarrow {\theta }^1={\theta }^0-\eta \nabla L\left({\theta }^0\right) \\ \left[\begin{array}{c}{\theta }_1^2\\ {\theta }_2^2\end{array}\right]=\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\end{array}\right]-\eta \left[\begin{array}{c}\partial L\left({\theta }_1^1\right)/\partial {\theta }_1\\ \partial L\left({\theta }_2^1\right)/\partial {\theta }_2\end{array}\right]\Rightarrow {\theta }^2={\theta }^1-\eta \nabla L\left({\theta }^1\right) \end{gathered}$$
在整个梯度下降的过程中，梯度不一定是递减的，但是沿着梯度下降的方向，函数值loss一定是递减的（如果学习率足够小），且当gradient=0时，loss下降到了局部最小值，梯度下降法指的是函数值loss随梯度下降的方向减小。初始随机在三维坐标系中选取一个点，这个三维坐标系的三个变量分别为$({\theta }_1,{\theta }_2,loss)$，我们的目标是找到最小的那个loss也就是三维坐标系中高度最低的那个点，而gradient梯度（Loss等高线的法线方向）可以理解为高度上升最快的那个方向，它的反方向就是梯度下降最快的那个方向，于是每次update沿着梯度反方向，update的步长由梯度大小和learning rate共同决定，当某次update完成后，该点的gradient=0，说明到达了局部最小值。

Tip 1: Tuning your learning rates

• 如果learning rate刚刚好，就可以顺利地到达到loss的最小值
• 如果learning rate太小的话，虽然最后能够走到local minimal处，但可能会迭代得非常慢，以至于你无法接受
• 如果learning rate太大，它的步伐太大了，它永远没有办法走到特别低的地方，可能永远在这个「山谷」的口上振荡而无法走下去
• 如果learning rate非常大，可能一瞬间就飞出去了，结果会造成update参数以后，loss反而会越来越大

当参数有很多个的时候(>3)，其实我们很难做到将loss随每个参数的变化可视化出来（因为最多只能可视化出三维的图像，也就只能可视化三维参数），但是我们可以把update的次数作为唯一的一个参数，将loss随着update的增加而变化的趋势给可视化出来

所以做梯度下降时，一个很重要的事情是，要把不同的learning rate下，loss随update次数的变化曲线给可视化出来，它可以提醒你该如何调整当前的learning rate的大小，直到出现稳定下降的曲线

Adaptive Learning rates

显然这样手动地去调整learning rates很麻烦，因此我们需要有一些「自动调整learning rates」的方法，最基本、最简单的大原则是：learning rate通常是随着参数的update越来越小的。因为在起始点的时候，通常是离最低点是比较远的，这时候步伐就要跨大一点；而经过几次update以后，会比较靠近目标，这时候就应该减小learning rate，让它能够收敛在最低点的地方。

举例：假设到了第t次update，此时${\eta }^t=\eta /\sqrt{t+1}$

这种方法使所有参数以同样的方式同样的learning rate进行迭代更新，而最好的状况是每个参数都给它不同的learning rate去迭代更新。

Adagrad

Divide the learning rate of each parameter by the root mean square(方均根) of its previous derivatives

Adagrad就是将不同参数的learning rate分开考虑的一种算法（adagrad算法update到后面速度会越来越慢，当然这只是adaptive算法中最简单的一种）

这里的$\omega$是function中的某个参数，$t$表示第 $t$ 次update，$g^t$表示Loss对$\omega$的偏微分，而${\sigma }^t$是之前所有Loss对$\omega$偏微分的方均根(根号下的平方均值)，这个值对每一个参数来说都是不一样的。

由于${\eta }^t$和${\sigma }^t$中都有一个$\sqrt{\frac{1}{1+t}}$的因子，两者相消，即可得到adagrad的最终表达式：
$$w^{t+1}=w^t-\frac{\eta }{\sqrt{\sum _{i=0}^t(g^i{)}^2}}\cdot g^t$$

Adagrad的表达式$w^{t+1}=w^t-\frac{\eta }{\sqrt{\sum _{i=0}^t(g^i{)}^2}}\cdot g^t$里面有一件很矛盾的事情：我们在做梯度下降的时候，希望的是当梯度值即微分值$g^t$越大的时候（此时斜率越大，还没有接近最低点）更新的步伐要更大一些，但是Adagrad的表达式中，分母表示梯度越大步伐越小，分子却表示梯度越大步伐越大，两者似乎相互矛盾。

在一些paper里是这样解释的：Adagrad要考虑的是，这个gradient有多surprise，即反差有多大，假设t=4的时候$g^4$与前面的gradient反差特别大，那么$g^t$与$\sqrt{\frac{1}{t+1}\sum _{i=0}^t(g^i{)}^2}$之间的大小反差就会比较大，它们的商就会把这一反差效果体现出来。同时，gradient越大，离最低点越远这件事情在有多个参数的情况下是不一定成立的。实际上，对于一个二次函数$y=a{x}^2+bx+c$来说，最小值点的$x=-\frac{b}{2a}$，而对于任意一点$x_0$，它迈出最好的步伐长度是$|x_0+\frac{b}{2a}|=|\frac{2a{x}_0+b}{2a}|$(这样就一步迈到最小值点了)，联系该函数的一阶和二阶导数$y^{\prime }=2ax+b$、$y^{\prime \prime }=2a$，可以发现the best step is $|\frac{y^{\prime }}{y^{\prime \prime }}|$，也就是说他不仅跟一阶导数(gradient)有关，还跟二阶导数有关。

再来回顾Adagrad的表达式：
$$w^{t+1}=w^t-\frac{\eta }{\sqrt{\sum _{i=0}^t(g^i{)}^2}}\cdot g^t$$

$g^t$就是一次微分，而分母中的$\sum _{i=0}^t(g^i{)}^2$反映了二次微分的大小，所以Adagrad想要做的事情就是，在不增加任何额外运算的前提下，想办法去估测二次微分的值。

Tip 2: Stochastic Gradient Descent（随即梯度下降SGD）

随机梯度下降的方法可以让训练更快速，传统的gradient descent的思路是看完所有的样本点之后再构建loss function，然后去update参数；而SGD的做法是，看到一个样本点就update一次，因此它的loss function不是所有样本点的error平方和，而是这个随机样本点的error平方。

Tip 3: Mini-batch Gradient Descent

这里有一个秘密，就是我们在做deep learning的梯度下降时，并不会真的去minimize total loss，那我们做的是什么呢？我们会把Training data分成一个一个的batch，比如你的Training data一共有一万张image，每次random选100张image作为一个batch：

• 像梯度下降一样，先随机initialize network的参数
• 选第一个batch出来，然后计算这个batch里面的所有element的total loss，$L^{\prime }=l^1+l^{31}+...$，接下来根据$L^{\prime }$去update参数，也就是计算$L^{\prime }$对所有参数的偏微分，然后update参数。（注意：$L^{\prime }$不是全部data的total loss）
• 再选择第二个batch，现在这个batch的total loss是$L^{\prime \prime }=l^2+l^{16}+...$，接下来计算$L^{\prime \prime }$对所有参数的偏微分，然后update参数
• 反复重复这个过程，直到把所有的batch通通选过一次，所以假设你有100个batch的话，你就把这个参数update 100次，把所有batch看过一次，就叫做一个epoch
• 重复epoch的过程，所以你在train network的时候，你会需要好几十个epoch，而不是只有一个epoch

整个训练的过程类似于SGD随即梯度下降，不是将所有数据读完才开始做「梯度下降」的，而是拿到一部分数据就做一次「梯度下降」。

Batch size and Training Speed

batch size太小会导致不稳定，速度上也没有优势

前面已经提到了，SGD速度快，表现好，既然如此，为什么我们还要用Mini-batch呢？这就涉及到了一些实际操作上的问题，让我们必须去用Mini-batch。举例来说，我们现在有50000个examples，如果我们把batch size设置为1，就是SGD，那在一个epoch里面，就会update 50000次参数；如果我们把batch size设置为10，在一个epoch里面，就会update 5000次参数。看上去SGD的速度貌似是比较快的，它一个epoch更新参数的次数比batch size等于10的情况下要快了10倍，但是我们好像忽略了一个问题，我们之前一直都是下意识地认为不同batch size的情况下运行一个epoch的时间应该是相等的，然后我们才去比较每个epoch所能够update参数的次数，可是它们又怎么可能会是相等的呢？

实际上，当你batch size设置不一样的时候，一个epoch需要的时间是不一样的，以GTX 980为例

• case 1：如果batch size设为1，也就是SGD，一个epoch要花费166秒，接近3分钟

• case 2：如果batch size设为10，那一个epoch是17秒

也就是说，当stochastic gradient descent算了一个epoch的时候，batch size为10的情况已经算了近10个epoch了。所以case 1跑一个epoch，做了50000次update参数的同时，case 2跑了十个epoch，做了近5000*10=50000次update参数；你会发现batch size设1和设10，update参数的次数几乎是一样的。

如果不同batch size的情况，update参数的次数几乎是一样的，你其实会想要选batch size更大的情况，相较于batch size=1，你会更倾向于选batch size=10，因为batch size=10的时候，是会比较稳定的，因为由更大的数据集计算的梯度能够更好的代表样本总体，从而更准确的朝向极值所在的方向。我们之前把gradient descent换成stochastic gradient descent，是因为后者速度比较快，update次数比较多，可是现在如果你用stochastic gradient descent并没有见得有多快，那你为什么不选一个update次数差不多，又比较稳定的方法呢？

batch size会受到GPU平行加速的限制，太大可能导致在train的时候卡住

上面例子的现象产生的原因是我们用了GPU，用了平行运算，所以batch size=10的时候，这10个example其实是同时运算的，所以你在一个batch里算10个example的时间跟算1个example的时间几乎可以是一样的。那你可能会问，既然batch size越大，它会越稳定，而且还可以平行运算，那为什么不把batch size变得超级大呢？这里有两个claim：

• 第一个claim就是，如果你把batch size开到很大，最终GPU会没有办法进行平行运算，它终究是有自己的极限的，也就是说它同时考虑10个example和1个example的时间是一样的，但当它考虑10000个example的时候，时间就不可能还是跟1个example一样，因为batch size考虑到硬件限制，是没有办法无穷尽地增长的。

• 第二个claim是说，如果把batch size设的很大，在train gradient descent的时候，可能跑两下你的network就卡住了，就陷到saddle point或者local minima里面去了。

因为在neural network的error surface上面，如果你把loss的图像可视化出来的话，它并不是一个convex的optimization problem，不会像理想中那么平滑，实际上它会有很多的坑坑洞洞，如果你用的batch size很大，甚至是Full batch，那你走过的路径会是比较平滑连续的，可能这一条平滑的曲线在走向最低点的过程中就会在坑洞或是缓坡上卡住了；但是，如果你的batch size没有那么大，意味着你走的路线没有那么的平滑，有些步伐走的是随机性的，路径是会有一些曲折和波动的。可能在你走的过程中，它的曲折和波动刚好使得你绕过了那些saddle point或是local minima的地方；或者当你陷入不是很深的local minima或者没有遇到特别麻烦的saddle point的时候，它步伐的随机性就可以帮你跳出这个gradient接近于0的区域，于是你更有可能真的走向global minima的地方。而对于Full batch的情况，它的路径是没有随机性的，是稳定朝着目标下降的，因此在这个时候去train neural network其实是有问题的，可能update两三次参数就会卡住，所以mini batch是有必要的。

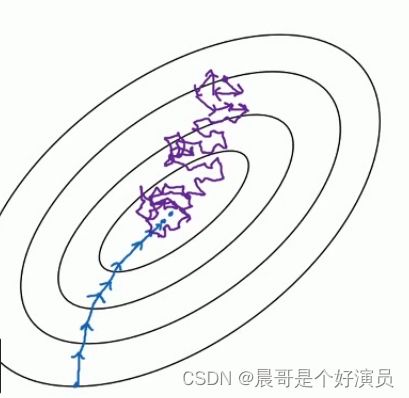
如下图，左边是full batch(拿全部的Training data做一个batch)的梯度下降效果，可以看到每一次迭代成本函数都呈现下降趋势，这是好的现象，说明我们$\omega$和$b$的设定一直再减少误差， 这样一直迭代下去我们就可以找到最优解；右边是mini batch的梯度下降效果，可以看到它是上下波动的，成本函数的值有时高有时低，但总体还是呈现下降的趋势， 这个也是正常的，因为我们每一次梯度下降都是在min batch上跑的而不是在整个数据集上， 数据的差异可能会导致这样的波动(可能某段数据效果特别好，某段数据效果不好)，但没关系，因为它整体是呈下降趋势的。

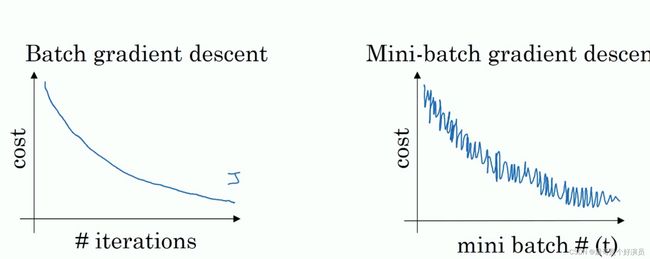
把下面的图看做是梯度下降空间：蓝色部分是full batch而紫色部分是mini batch，就像上面所说的mini batch不是每次迭代损失函数都会减少，所以看上去好像走了很多弯路，不过整体还是朝着最优解迭代的，而且由于mini batch一个epoch就走了5000步（5000次梯度下降），而full batch一个epoch只有一步，所以虽然mini batch走了弯路但还是会快很多。而且，就像之前提到的那样，mini batch在update的过程中，步伐具有随机性，因此紫色的路径可以在一定程度上绕过或跳出saddle point、local minima这些gradient趋近于0的地方；而蓝色的路径因为缺乏随机性，只能按照既定的方式朝着目标前进，很有可能就在中途被卡住，永远也跳不出来了。

当然，如果batch size太小，会造成速度不仅没有加快反而会导致下降的曲线更加不稳定的情况产生。因此batch size既不能太大，因为它会受到硬件GPU平行加速的限制，导致update次数过于缓慢，并且由于缺少随机性而很容易在梯度下降的过程中卡在saddle point或是local minima的地方；而且batch size也不能太小，因为它会导致速度优势不明显的情况下，梯度下降曲线过于不稳定，算法可能永远也不会收敛。

Speed - Matrix Operation

整个network，不管是Forward pass还是Backward pass，都可以看做是一连串的矩阵运算的结果。那今天我们就可以比较batch size等于1（stochastic gradient descent）和10（mini batch）的差别。

如下图所示，stochastic gradient descent就是对每一个input x进行单独运算；而mini batch，则是把同一个batch里面的input全部集合起来，假设现在我们的batch size是2，那mini batch每一次运算的input就是把黄色的vector和绿色的vector拼接起来变成一个matrix，再把这个matrix乘上$w_1$，你就可以直接得到$z^1$和$z^2$。

这两件事在理论上运算量是一样多的，但是在实际操作上，对GPU来说，在矩阵里面相乘的每一个element都是可以平行运算的，所以图中stochastic gradient descent运算的时间反而会变成下面mini batch使用GPU运算速度的两倍，这就是为什么我们要使用mini batch的原因。

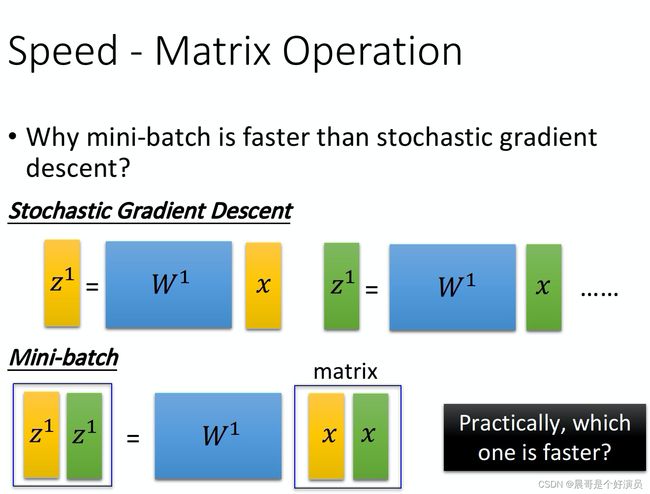
所以，如果你买了GPU，但是没有使用mini batch的话，其实就不会有多少加速的效果。

Tip 4: Feature Scaling特征缩放

特征缩放，当多个特征的分布范围很不一样时，最好将这些不同feature的范围缩放成一样。

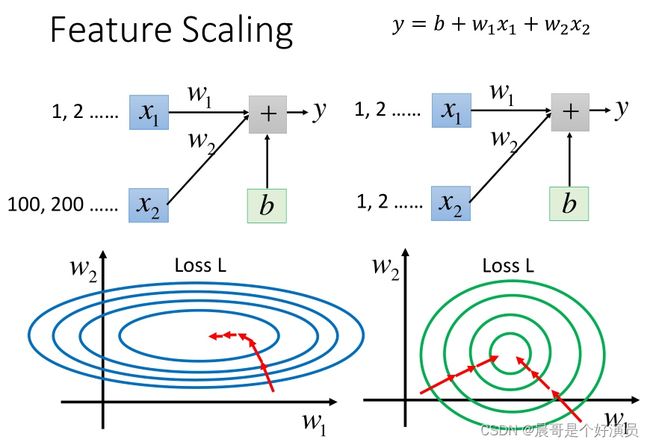
$y=b+w_1{x}_1+w_2{x}_2$，假设$x_1$的值都是很小的，比如1,2…；$x_2$的值都是很大的，比如100,200…

此时去画出loss的error surface，如果对$w_1$和$w_2$都做一个同样的变动$\Delta w$，那么$w_1$的变化对$y$的影响是比较小的，而$w_2$的变化对$y$的影响是比较大的。对于error surface表示，$w_1$对$y$的影响比较小，所以$w_1$对loss是有比较小的偏微分的，因此在$w_1$的方向上图像是比较平滑的；$w_2$对$y$的影响比较大，所以$w_2$对loss的影响比较大，因此在$w_2$的方向上图像是比较sharp的。如果$x_1$和$x_2$的值，它们的scale是接近的，那么$w_1$和$w_2$对loss就会有差不多的影响力，loss的图像接近于圆形，那这样做对gradient descent有什么好处呢？

对于长椭圆形的error surface，如果不使用Adagrad之类的方法，是很难搞定它的，因为在像$w_1$和$w_2$这样不同的参数方向上，会需要不同的learning rate，用相同的学习率很难达到最低点；如果有scale的话，loss在参数$w_1$、$w_2$平面上的投影就是一个正圆形，update参数会比较容易。而且gradient descent的每次update并不都是向着最低点走的，每次update的方向是顺着等高线的方向（梯度gradient下降的方向），而不是径直走向最低点；

但是当经过对input的scale使loss的投影是一个正圆的话，不管在这个区域的哪一个点，它都会向着圆心走。因此feature scaling对参数update的效率是有帮助的。

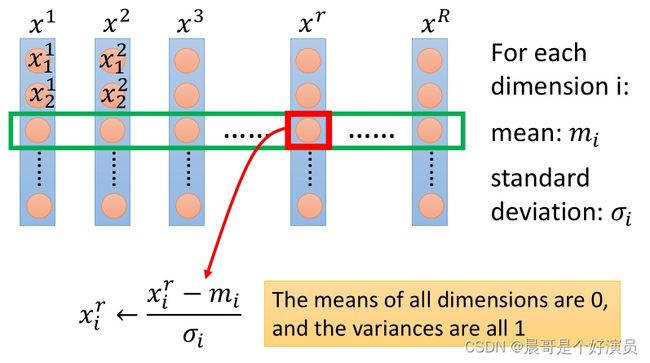
假设有$R$个example（上标i表示第$i$个样本点），$x^1,x^2,x^3,...,x^r,...x^R$，每一笔example，它里面都有一组feature（下标$j$表示该样本点的第$j$个特征）。对每一个dimension i，都去算出它的平均值mean $m_i$，以及标准差standard deviation ${\sigma }_i$，对第$r$个example的第$i$个component，减掉均值，除以标准差，即
$$x_i^r=\frac{x_i^r-m_i}{{\sigma }_i}$$

实际上就是将每一个参数都归一化成标准正态分布，即$f(x_i)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x_i^2}{2}}$，其中$x_i$表示第$i$个参数。

Gradient Descent Theory

When solving: ${\theta }^{\ast }=\arg {\min }_{\theta }L(\theta )$ by gradient descent, Each time we update the parameters, we obtain $\theta$ that makes $L(\theta )$ smaller.

$L\left({\theta }^0\right)>L\left({\theta }^1\right)>L\left({\theta }^2\right)>\cdots$

Is this statement correct? 不正确

Taylor Series

泰勒表达式：$h(x)=\sum _{k=0}^{\infty }\frac{h^{(k)}(x_0)}{k!}(x-x_0{)}^k=h(x_0)+h^{\prime }(x_0)(x-x_0)+\frac{h^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+...$

When x is close to $x_0$ : $h(x)\approx h(x_0)+h^{\prime }(x_0)(x-x_0)$

同理，对于二元函数，when x and y is close to $x_0$ and $y_0$：

$h(x,y)\approx h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0)$

Formal Derivation

对于loss图像上的某一个点(a,b)，如果我们想要找这个点附近loss最小的点，就可以用泰勒展开的思想。假设用一个red circle限定点的范围，这个圆足够小以满足泰勒展开的精度，那么此时我们的loss function就可以化简为：

$$L(\theta )\approx L(a,b)+\frac{\partial L(a,b)}{\partial {\theta }_1}({\theta }_1-a)+\frac{\partial L(a,b)}{\partial {\theta }_2}({\theta }_2-b)$$

令$s=L(a,b)$，$u=\frac{\partial L(a,b)}{\partial {\theta }_1}$，$v=\frac{\partial L(a,b)}{\partial {\theta }_2}$，则：
$$L(\theta )\approx s+u\cdot ({\theta }_1-a)+v\cdot ({\theta }_2-b)$$

假定red circle的半径为$d$，则有限制条件：$({\theta }_1-a{)}^2+({\theta }_2-b{)}^2\le d^2$。此时去求$L(\theta {)}_{min}$，这里有个小技巧，把$L(\theta )$转化为两个向量的乘积：
$$u\cdot ({\theta }_1-a)+v\cdot ({\theta }_2-b)=(u,v)\cdot ({\theta }_1-a,{\theta }_2-b)=(u,v)\cdot (\Delta {\theta }_1,\Delta {\theta }_2)$$

当向量$({\theta }_1-a,{\theta }_2-b)$与向量$(u,v)$反向，且刚好到达red circle的边缘时，$L(\theta )$最小。$({\theta }_1-a,{\theta }_2-b)$实际上就是$(\Delta {\theta }_1,\Delta {\theta }_2)$，于是$L(\theta )$局部最小值对应的参数为中心点减去gradient的加权，用$\eta$去控制向量的长度。
$$\left[\begin{array}{c}\Delta {\theta }_1\\ \Delta {\theta }_2\end{array}\right]=-\eta \left[\begin{array}{c}u\\ v\end{array}\right]\Rightarrow \left[\begin{array}{c}{\theta }_1\\ {\theta }_2\end{array}\right]=\left[\begin{array}{c}a\\ b\end{array}\right]-\eta \left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{c}a\\ b\end{array}\right]-\eta \left[\begin{array}{c}\frac{\partial L(a,b)}{\partial {\theta }_1}\\ \frac{\partial L(a,b)}{\partial {\theta }_2}\end{array}\right]$$
这就是gradient descent在数学上的推导，注意它的重要前提是，给定的那个红色圈圈的范围要足够小，这样泰勒展开给我们的近似才会更精确，而$\eta$的值是与圆的半径成正比的，因此理论上learning rate要无穷小才能够保证每次gradient descent在update参数之后的loss会越来越小，于是当learning rate没有设置好，泰勒近似不成立，就有可能使gradient descent过程中的loss没有越来越小。

当然泰勒展开可以使用二阶、三阶乃至更高阶的展开，但这样会使得运算量大大增加，反而降低了运行效率。

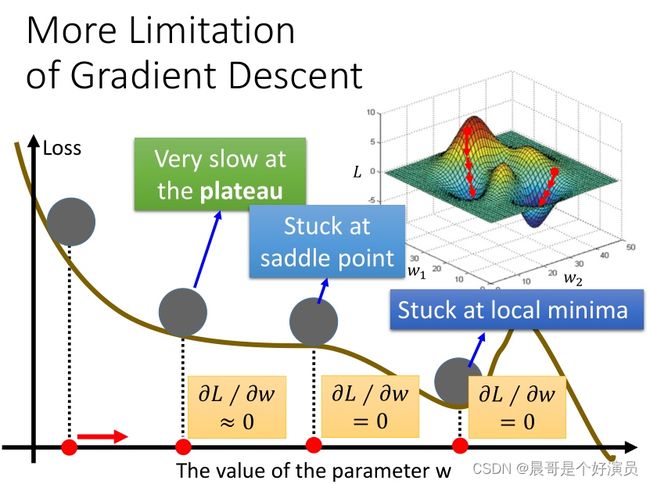
More Limitation of Gradient Descent

gradient descent的限制是，它在gradient即微分值接近于0的地方就会停下来，而这个地方不一定是global minima，它可能是local minima，可能是saddle point鞍点，甚至可能是一个loss很高的平缓高原。