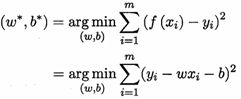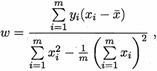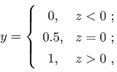吃瓜笔记:机器学习第三章:线性模型
机器学习第三章:线性模型
这一章也是本书基础理论的一章。我对本章末尾的一些公式含糊不清,但终于在不懈努力下得以理解。本章涵盖了线性代数和概率论的基础知识,并讨论了一些经典的线性模型、回归、分类问题(二分类和多重分类)。
3.1 基本形式
给定由d个属性描述的示例 x =(x1;x2;… ;xd),其中xi是x在第i个属性上的取值,线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数,即:
f ( x ) = w 1 x 1 + w 2 x 2 + … + w d x d + b f(x) = w_1x_1 + w_2x_2 + … + w_dx_d + b f(x)=w1x1+w2x2+…+wdxd+b
一般用向量形式写成:
f ( x ) = w T x + b f(x) = w_Tx + b f(x)=wTx+b
其中 x = ( x 1 ; x 2 ; … ; x d ) x =(x1;x2;… ;xd) x=(x1;x2;…;xd), w w w和 d d d学得之后,模型就得以确定。
线性模型,形式简单、易于建模,蕴含着机器学习中一些重要的基本思想,许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上通过引入层级结构或高维映射而得,此外,由于w直观表达了各属性在预测中的重要性,因此线性模型有很好的可解释性(comprehensibility)。例如在西瓜问题中学得“f好瓜(x) = 0.2x色泽 + 0.5x根蒂 + 0.3*x敲声 + 1”。
3.2 线性回归
给定一个数据集 D = {(x1, y1), (x2, y2), … , (xm, ym)},其中 xi = (xi1;xi2;…;xid), yi ∈ R。“线性回归” (linear regression)尝试学习一个线性模型,该模型尽可能准确地预测实值输出标签。
线性回归试图学得
![]()
我们要去确定w和b,在2.3节介绍过,均方误差(2.2)是回归任务中最常用的性能度量,因此我们可试图让均方误差最小化,即:
w*, b* 表示w和b的解。
均方误差,有非常好的几何意义,对应了常用的欧几里得距离或简称“欧氏距离(Euclidean method)”,在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧式距离之和最小。
求解w和b使![]() 最小化的过程,叫做线性回归模型的最小二乘“参数估计(parameter estimate)”,然后E(w, b)分别对w和b求导,得到:
最小化的过程,叫做线性回归模型的最小二乘“参数估计(parameter estimate)”,然后E(w, b)分别对w和b求导,得到:
然后令上面两个式子为零,求得w和b最优解的闭式(closed-form)解:
其中 ![]() 为x的均值。
为x的均值。
更一般的,数据集D,样本由d个属性描述,此时我们试图学得:
![]()
这称为“多元线性回归(multivariate linear regression)”(这部分涉及公式教繁,线性代数知识具体推导书上)
我们希望线性模型的预测值逼近真实标记y时,就得到了线性回归模型,为便于观察,写作:
![]()
我们要让输出标记y在指数尺度上变化,可做变化:
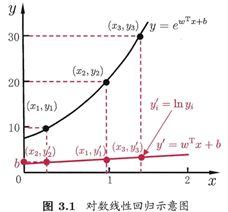
这就是“对数线性回归(log-linear regression)”,它实际上是在试图让![]() 逼近y,下图很明了:
逼近y,下图很明了:
更一般的,考虑单调可微函数g(*),令:
![]()
这样得到的模型称为“广义线性模型(generalized linear model)”,其中函数g(),称为“联系函数(link function)”。显然,对数线性回归是广义线性模型在g() = ln(*)时的特例。
3.3 对数线性回归
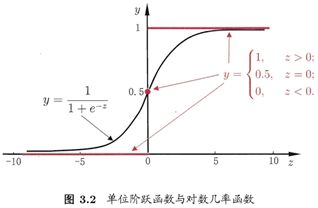
考虑二分类任务,其输出标记y∈{0, 1},而线性回归模型产生的预测值 是实值,于是,我们需将实值转换为0/1值,最理想是“单位阶跃函数(unit-step function)”
即如果预测值z大于零,则判断为正例,如果小于零,则判断为反例,临界值可以任意判断预测值z,如图下图:
对数几率函数(logistic function)是这样一个常用的替代函数:
将对数几率函数作为g-(*)带入,得:
整理一下:
若将y视为样本x作为正例的可能性,则1-y是其反例可能性,两者比值:
称为“几率(odds)”,反映了样本x作为正例的相对可能性,然后对几率取对数得“对数几率(log odds,也称logit)”:
由此看出,实际上面在用线性回归模型的预测结果去逼近真实标记的对数几率,因此,其对应的模型称为“对数几率回归(logistic regression,也称logit regression)”。要注意的是,虽然它的名字是“回归”,但实际上确实一种分类学习方法。
3.4 线性判别分析
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的线性学习方法,在二分类问题上最早由[Fisher, 1936]提出,所以也叫做“Fisher判别分析”。
LDA的思想很简单:给定一组训练模式,尝试将这些模式投影到一条直线上,使得相似模式的投影点尽可能接近,异种模式的投影点尽可能远,尽可能看清楚:
3.5 多分类学习
现实中常见遇到多分类任务。有些二分类学习方法可直接推广到多分类。但多数情况下,要基于一些基本策略,利用二分类学习器来解决多分类问题。
不失一般性,考虑N个类别C1, C2, … , CN,多分类学习的基本思路是“拆解法”,即将多分类任务拆分为若干个二分类任务求解。最经典的拆分策略有三种:“一对一(One vs. One,简称OvO)”、“一对余(One vs. Rest,简称OvR)”和“多对多(Many vs. Many,简称MvM)”。
多分类学习有两个思路。一种是将二分类学习方法推广到多分类,比如上一节讲到的LDA。另一种则是利用二分类的学习器来解决多分类问题。下面主要讨论第二种。
1、拆解法与拆分策略
拆解法:将多分类任务拆解成为若干个二分类任务求解。
拆解法步骤:
1.通过拆分策略对问题进行【拆分】;
2.为拆分出的每个二分类任务【**训练】**一个分类器;
3.对各个分类器的结果进行【集成】,以获得多分类结果。
(牢记这三个关键词。)
最经典的拆分策略有三种,即“一对一(OvO)”、“一对其余(OvR)”、“多对多(MvM)”。
多分类学习有 N N N个类别 C 1 , C 2 , . . . , C N C_1,C_2,...,C_N C1,C2,...,CN,给定数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , y i ∈ { C 1 , C 2 , . . . , C n } D=\{(\boldsymbol x_1,y_1),(\boldsymbol x_2,y_2),...,(\boldsymbol x_m,y_m)\},y_i\in\{C_1,C_2,...,C_n\} D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{C1,C2,...,Cn}
1、OvO:
将 N N N个分类分别两两配对,从而【**拆分】**成 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2个二分类任务;【训练】时为了区分 C i C_i Ci和 C j C_j Cj这两个分类,这 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2个分类器中的一个将 C i C_i Ci作为正例, C j C_j Cj 作为反例;测试时候将新样本同时提交给所有分类器,将得到 N ( N − 1 ) / 2 N(N-1)/2 N(N−1)/2个分类结果,【**集成】**的方法是通过投票在这些结果中选出最终结果。
2、OvR:
将 N N N 个分类中的1个类拿出来作为一个分类器的正例,其余均设置为反例,从而【拆分】成 N N N 个分类任务;【训练】得到 N N N 个分类结果;【集成】的方法是考虑各被判为正例的分类器的置信度,选择置信度大的类别标记作为分类的结果。(如只有一个,直接选择)
OvO与OvR示意图
3、MvM:
MvM是OvO和OvR的一般形式,反过来说,OvO和OvR是MvM的特例。
MvM每次将若干个类作为正类,若干个其他类作为反类。但其构造必须有特殊的设计,不能随意选取。常用的一种MvM技术是“纠错输出码”(ECOC)技术。
2、“纠错输出码”(ECOC)技术
ECOC过程主要分两步:
编码:对 N N N 个类进行 M M M 次划分,产生 M M M 个分类器;
解码: M M M 个分类器对测试样本进行预测,得到 M M M 个预测标记,将其组成编码;这个编码与 N N N 个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测的结果。
编码形式又分为二元码和三元码,前者指定“正类”、“反类”,后者又多一个“停用类”。
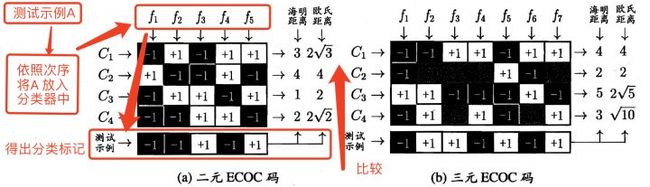
以二元ECOC码为例:如下图,首先,将 N N N ( N = 4 N=4 N=4 )个类通过设计构造成 M M M ( M = 5 M=5 M=5 )个分类器( f 1 , f 2 , f 3 , f 4 , f 5 f_1,f_2,f_3,f_4,f_5 f1,f2,f3,f4,f5 ),每个分类器为每个类分配了一个标记结果( − 1 -1 −1 或 + 1 +1 +1 ),这样一来,每一个类 C i , i ∈ { 1 , N } C_i,i\in\{1,N\} Ci,i∈{1,N} 都获得了一个 M M M 位的编码,这个编码就是【各类所对应的编码】。
当有一个测试例 A A A 的时,先将 A A A 依照次序放入 M M M 个分类器中,得到了 M M M 个分类标记结果(-1,-1,+1,-1,+1);再将这 M M M 个标记结果编成一个纠错输出码(-1,-1,+1,-1,+1);最后去和【各类所对应的编码】进行比较海明距离或欧式距离,距离最短的对应编码对应的分类就是结果。(图中结果为 C 3 C_3 C3 )
ECOC编码示意图
纠错输出码还有一个功能是为分类器的错误进行修正。比如正确的分类结果是(-1,-1,+1,-1,+1),但如果分类器 f 2 f_2 f2 出了错误,得到的结果就是(-1,+1,+1,-1,+1)。但通过这一套编码,可以让最终的结果仍为 C 3 C_3 C3 。
分类器越多,ECOC编码越长,纠错能力越强,但开销越大;而且,如果分类有限,那么可组合的数目也有限,码长超过一定程度,也没有意义了。
同等长度的编码,【各类所对应的编码】之间计算出的距离越远,编码的纠错能力越强,但当码长到达一定程度时,无法得出最优解。
3.6、类别不平衡问题
以二分类问题为例,该问题一般指的是训练集中正负样本数比例相差过大(比如正例9998个,负例2个),其一般会造成以下的一些情况:
1. 类别少的误判惩罚过低,导致有所偏袒,当样本不确定时倾向于把样本分类为多数类。
2. 样本数量分布很不平衡时,特征的分布同样会不平衡。
3. 传统的评价指标变得不可靠,例如准确率。
而在多分类问题中,尽管原始训练集中可能不同类别训练样本数目相当,通过OvR、MvM进行拆分时也有可能会造成上述情况,所以类别不平衡问题亟待解决。
解决类别不平衡问题一个基本思路是“再缩放”。
线性模型解决二分类问题中,我们通常将得到一个预测值 y y y 或 y y y 的衍生物,将其与某个固定值比较,来判断其为正例还是反例。
如果说将 y y y 看做样本 x \boldsymbol x x 作为正例的可能性,那么 1 − y 1-y 1−y 就是其成为反例的可能性。
两者的比值称为“几率”,反映了样本作为正例的相对可能性。
几 率 = 正 例 可 能 性 反 例 可 能 性 = y 1 − y 几率=\frac{正例可能性}{反例可能性}=\frac{y}{1-y} 几率=反例可能性正例可能性=1−yy
正反例数目相同时,当其大于1时,可预测为正例,反之预测为反例;
但当正反例数目不同时, m + m^+ m+ 代表正例数目, m − m^- m− 代表反例数目,观测几率应是 m + m − \frac{m^+}{m^-} m−m+ ,而只要分类器的预测几率 y y − 1 \frac{y}{y-1} y−1y 大于观测几率,就应判定为正例。
故,实际情况需对决策进行调整,变为: y ′ y ′ − 1 = y y − 1 × m − m + \frac{y'}{y'-1}=\frac{y}{y-1}\times \frac{m^-}{m^+} y′−1y′=y−1y×m+m−
综上,第三章内容还是很丰富的,要记得复习,实操,转化成自己的知识。
加油!