决策树——预剪枝和后剪枝
一、 为什么要剪枝
1、未剪枝存在的问题
决策树生成算法递归地产生决策树,直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确,但对未知的测试数据的分类却没有那么准确,即容易出现过拟合现象。解决这个问题的办法是考虑决策树的复杂度,对已生成的决策树进行简化,下面来探讨以下决策树剪枝算法。
2、剪枝的目的
决策树的剪枝是为了简化决策树模型,避免过拟合。
- 同样层数的决策树,叶结点的个数越多就越复杂;同样的叶结点个数的决策树,层数越多越复杂。
- 剪枝前相比于剪枝后,叶结点个数和层数只能更多或者其中一特征一样多,剪枝前必然更复杂。
- 层数越多,叶结点越多,分的越细致,对训练数据分的也越深,越容易过拟合,导致对测试数据预测时反而效果差,泛化能力差。
3、剪枝算法实现思路
剪去决策树模型中的一些子树或者叶结点,并将其上层的根结点作为新的叶结点,从而减少了叶结点甚至减少了层数,降低了决策树复杂度。
在决策树的建立过程中不断调节来达到最优,可以调节的条件有:
- 树的深度:在决策树建立过程中,发现深度超过指定的值,那么就不再分了。
- 叶子节点个数:在决策树建立过程中,发现叶子节点个数超过指定的值,那么就不再分了。
- 叶子节点样本数:如果某个叶子结点的个数已经低于指定的值,那么就不再分了。
- 信息增益量或Gini系数:计算信息增益量或Gini系数,如果小于指定的值,那就不再分了。
二、预剪枝
预剪枝是在决策树生成过程中,对树进行剪枝,提前结束树的分支生长。其中的核心思想就是,在每一次实际对结点进行进一步划分之前,先采用验证集的数据来验证划分是否能提高划分的准确性。如果不能,就把结点标记为叶结点并退出进一步划分;如果可以就继续递归生成节点。加入预剪枝后的决策树生成流程图如下:

优点:预剪枝可以有效降低过拟合现象,在决策树建立过程中进行调节,因此显著减少了训练时间和测试时间;预剪枝效率比后剪枝高。
缺点:预剪枝是通过限制一些建树的条件来实现的,这种方式容易导致欠拟合现象:模型训练的不够好。
三、后剪枝
在决策树建立完成之后再进行的,根据以下公式:
C = gini(或信息增益)*sample(样本数) + a*叶子节点个数
C表示损失,C越大,损失越多。通过剪枝前后的损失对比,选择损失小的值,考虑是否剪枝。
a是自己调节的,a越大,叶子节点个数越多,损失越大。因此a值越大,偏向于叶子节点少的,a越小,偏向于叶子节点多的。
后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情况下,后剪枝决策树的欠拟合风险很小,泛化性能往往由于预剪枝决策树,但是后剪枝过程是在生成完全决策树后进行的,并且要自下往上地对树中的非叶子节点逐一进行考察计算,因此训练时间的开销比为剪枝和预剪枝决策树都要大得多。
四、代码实现
1、未剪枝
可视化树:
import matplotlib.pyplot as plt
decisionNodeStyle = dict(boxstyle = "sawtooth", fc = "0.8")
leafNodeStyle = {"boxstyle": "round4", "fc": "0.8"}
arrowArgs = {"arrowstyle": "<-"}
# 画节点
def plotNode(nodeText, centerPt, parentPt, nodeStyle):
createPlot.ax1.annotate(nodeText, xy = parentPt, xycoords = "axes fraction", xytext = centerPt
, textcoords = "axes fraction", va = "center", ha="center", bbox = nodeStyle, arrowprops = arrowArgs)
# 添加箭头上的标注文字
def plotMidText(centerPt, parentPt, lineText):
xMid = (centerPt[0] + parentPt[0]) / 2.0
yMid = (centerPt[1] + parentPt[1]) / 2.0
createPlot.ax1.text(xMid, yMid, lineText)
# 画树
def plotTree(decisionTree, parentPt, parentValue):
# 计算宽与高
leafNum, treeDepth = getTreeSize(decisionTree)
# 在 1 * 1 的范围内画图,因此分母为 1
# 每个叶节点之间的偏移量
plotTree.xOff = plotTree.figSize / (plotTree.totalLeaf - 1)
# 每一层的高度偏移量
plotTree.yOff = plotTree.figSize / plotTree.totalDepth
# 节点名称
nodeName = list(decisionTree.keys())[0]
# 根节点的起止点相同,可避免画线;如果是中间节点,则从当前叶节点的位置开始,
# 然后加上本次子树的宽度的一半,则为决策节点的横向位置
centerPt = (plotTree.x + (leafNum - 1) * plotTree.xOff / 2.0, plotTree.y)
# 画出该决策节点
plotNode(nodeName, centerPt, parentPt, decisionNodeStyle)
# 标记本节点对应父节点的属性值
plotMidText(centerPt, parentPt, parentValue)
# 取本节点的属性值
treeValue = decisionTree[nodeName]
# 下一层各节点的高度
plotTree.y = plotTree.y - plotTree.yOff
# 绘制下一层
for val in treeValue.keys():
# 如果属性值对应的是字典,说明是子树,进行递归调用; 否则则为叶子节点
if type(treeValue[val]) == dict:
plotTree(treeValue[val], centerPt, str(val))
else:
plotNode(treeValue[val], (plotTree.x, plotTree.y), centerPt, leafNodeStyle)
plotMidText((plotTree.x, plotTree.y), centerPt, str(val))
# 移到下一个叶子节点
plotTree.x = plotTree.x + plotTree.xOff
# 递归完成后返回上一层
plotTree.y = plotTree.y + plotTree.yOff
# 画出决策树
def createPlot(decisionTree):
fig = plt.figure(1, facecolor = "white")
fig.clf()
axprops = {"xticks": [], "yticks": []}
createPlot.ax1 = plt.subplot(111, frameon = False, **axprops)
# 定义画图的图形尺寸
plotTree.figSize = 1.5
# 初始化树的总大小
plotTree.totalLeaf, plotTree.totalDepth = getTreeSize(decisionTree)
# 叶子节点的初始位置x 和 根节点的初始层高度y
plotTree.x = 0
plotTree.y = plotTree.figSize
plotTree(decisionTree, (plotTree.figSize / 2.0, plotTree.y), "")
plt.show()
2、预剪枝
创建预剪枝决策树
def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'):
trainData = np.asarray(dataTrain)
labelTrain = np.asarray(labelTrain)
testData = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 如果结果为单一结果
if len(set(labelTrain)) == 1:
return labelTrain[0]
# 如果没有待分类特征
elif trainData.size == 0:
return voteLabel(labelTrain)
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据最优特征进行分割
dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat)
# 预剪枝评估
# 划分前的分类标签
labelTrainLabelPre = voteLabel(labelTrain)
labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size
# 划分后的精度计算
if dataTest is not None:
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat)
# 划分前的测试标签正确比例
labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size
# 划分后 每个特征值的分类标签正确的数量
labelTrainEqNumPost = 0
for val in labelTrainSet.keys():
labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0
# 划分后 正确的比例
labelTestRatioPost = labelTrainEqNumPost / labelTest.size
# 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分
if dataTest is None and labelTrainRatioPre == 0.5:
decisionTree = {bestFeatName: {}}
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, None, None, names, method)
elif dataTest is None:
return labelTrainLabelPre
# 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回
elif labelTestRatioPost < labelTestRatioPre:
return labelTrainLabelPre
else :
# 根据选取的特征名称创建树节点
decisionTree = {bestFeatName: {}}
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataTrainSet.keys():
decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue)
, dataTestSet.get(featValue), labelTestSet.get(featValue)
, names, method)
return decisionTree
测试:
xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest = splitXgData20(xgData, xgLabel)
# 生成不剪枝的树
xgTreeTrain = createTree(xgDataTrain, xgLabelTrain, xgName, method = 'id3')
# 生成预剪枝的树
xgTreePrePruning = createTreePrePruning(xgDataTrain, xgLabelTrain, xgDataTest, xgLabelTest, xgName, method = 'id3')
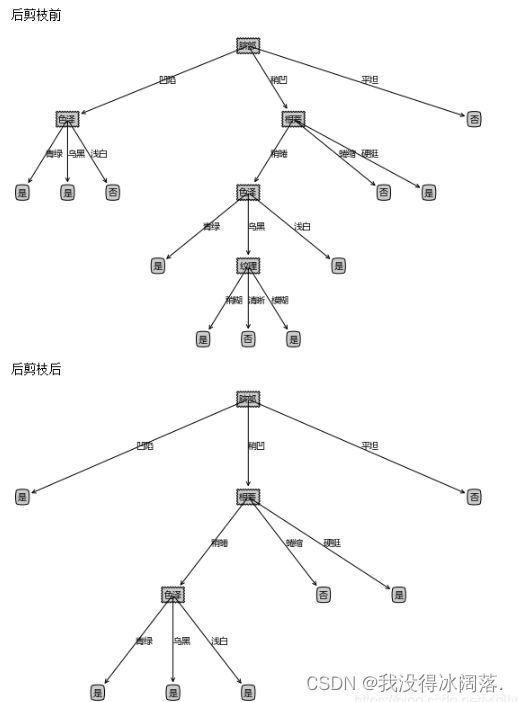
# 画剪枝前的树
print("剪枝前的树")
createPlot(xgTreeTrain)
# 画剪枝后的树
print("剪枝后的树")
createPlot(xgTreePrePruning)
3、后剪枝
# 创建决策树 带预划分标签
def createTreeWithLabel(data, labels, names, method = 'id3'):
data = np.asarray(data)
labels = np.asarray(labels)
names = np.asarray(names)
# 如果不划分的标签为
votedLabel = voteLabel(labels)
# 如果结果为单一结果
if len(set(labels)) == 1:
return votedLabel
# 如果没有待分类特征
elif data.size == 0:
return votedLabel
# 其他情况则选取特征
bestFeat, bestEnt = bestFeature(data, labels, method = method)
# 取特征名称
bestFeatName = names[bestFeat]
# 从特征名称列表删除已取得特征名称
names = np.delete(names, [bestFeat])
# 根据选取的特征名称创建树节点 划分前的标签votedPreDivisionLabel=_vpdl
decisionTree = {bestFeatName: {"_vpdl": votedLabel}}
# 根据最优特征进行分割
dataSet, labelSet = splitFeatureData(data, labels, bestFeat)
# 对最优特征的每个特征值所分的数据子集进行计算
for featValue in dataSet.keys():
decisionTree[bestFeatName][featValue] = createTreeWithLabel(dataSet.get(featValue), labelSet.get(featValue), names, method)
return decisionTree
# 将带预划分标签的tree转化为常规的tree
# 函数中进行的copy操作,原因见有道笔记 【YL20190621】关于Python中字典存储修改的思考
def convertTree(labeledTree):
labeledTreeNew = labeledTree.copy()
nodeName = list(labeledTree.keys())[0]
labeledTreeNew[nodeName] = labeledTree[nodeName].copy()
for val in list(labeledTree[nodeName].keys()):
if val == "_vpdl":
labeledTreeNew[nodeName].pop(val)
elif type(labeledTree[nodeName][val]) == dict:
labeledTreeNew[nodeName][val] = convertTree(labeledTree[nodeName][val])
return labeledTreeNew
# 后剪枝 训练完成后决策节点进行替换评估 这里可以直接对xgTreeTrain进行操作
def treePostPruning(labeledTree, dataTest, labelTest, names):
newTree = labeledTree.copy()
dataTest = np.asarray(dataTest)
labelTest = np.asarray(labelTest)
names = np.asarray(names)
# 取决策节点的名称 即特征的名称
featName = list(labeledTree.keys())[0]
# print("\n当前节点:" + featName)
# 取特征的列
featCol = np.argwhere(names==featName)[0][0]
names = np.delete(names, [featCol])
# print("当前节点划分的数据维度:" + str(names))
# print("当前节点划分的数据:" )
# print(dataTest)
# print(labelTest)
# 该特征下所有值的字典
newTree[featName] = labeledTree[featName].copy()
featValueDict = newTree[featName]
featPreLabel = featValueDict.pop("_vpdl")
# print("当前节点预划分标签:" + featPreLabel)
# 是否为子树的标记
subTreeFlag = 0
# 分割测试数据 如果有数据 则进行测试或递归调用 np的array我不知道怎么判断是否None, 用is None是错的
dataFlag = 1 if sum(dataTest.shape) > 0 else 0
if dataFlag == 1:
# print("当前节点有划分数据!")
dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, featCol)
for featValue in featValueDict.keys():
# print("当前节点属性 {0} 的子节点:{1}".format(featValue ,str(featValueDict[featValue])))
if dataFlag == 1 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# 如果是子树则递归
newTree[featName][featValue] = treePostPruning(featValueDict[featValue], dataTestSet.get(featValue), labelTestSet.get(featValue), names)
# 如果递归后为叶子 则后续进行评估
if type(featValueDict[featValue]) != dict:
subTreeFlag = 0
# 如果没有数据 则转换子树
if dataFlag == 0 and type(featValueDict[featValue]) == dict:
subTreeFlag = 1
# print("当前节点无划分数据!直接转换树:"+str(featValueDict[featValue]))
newTree[featName][featValue] = convertTree(featValueDict[featValue])
# print("转换结果:" + str(convertTree(featValueDict[featValue])))
# 如果全为叶子节点, 评估需要划分前的标签,这里思考两种方法,
# 一是,不改变原来的训练函数,评估时使用训练数据对划分前的节点标签重新打标
# 二是,改进训练函数,在训练的同时为每个节点增加划分前的标签,这样可以保证评估时只使用测试数据,避免再次使用大量的训练数据
# 这里考虑第二种方法 写新的函数 createTreeWithLabel,当然也可以修改createTree来添加参数实现
if subTreeFlag == 0:
ratioPreDivision = equalNums(labelTest, featPreLabel) / labelTest.size
equalNum = 0
for val in labelTestSet.keys():
equalNum += equalNums(labelTestSet[val], featValueDict[val])
ratioAfterDivision = equalNum / labelTest.size
# print("当前节点预划分标签的准确率:" + str(ratioPreDivision))
# print("当前节点划分后的准确率:" + str(ratioAfterDivision))
# 如果划分后的测试数据准确率低于划分前的,则划分无效,进行剪枝,即使节点等于预划分标签
# 注意这里取的是小于,如果有需要 也可以取 小于等于
if ratioAfterDivision < ratioPreDivision:
newTree = featPreLabel
return newTree
五、两种算法对比
- 后剪枝决策树通常比预剪枝决策树保留了更多的分支;
- 后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树;
- 后剪枝决策树训练时间开销比未剪枝决策树和预剪枝决策树都要大的多。