天津理工大学 信息论与编码实验1 离散信源的统计度量-自信量和熵的计算

一、实验目的
离散无记忆信源是一种最简单且最重要的信源，可以用完备的离散型概率空间来描述。本实验通过计算给定的信源的熵，加深对信源熵概念的理解。
熟悉Matlab等基础编程。

二、实验仪器及材料
计算机

三、实验原理
信源输出的各消息的自信息量的数学期望为信源的信息熵，表达式如下

信源熵是信源的统计平均不确定性的描述，是概率 的函数。

四、实验内容
写出实验内容中的程序并附上实现的结果。

1、请分别完成离散信源自信息量及信源熵，以Matlab函数为例：
function [I] = selfInfo§
% 自信息量函数，P为概率分布，I为信源各状态下的自信息量。如输入P = [1/2, 1/2]
% 则输出为1 1

function [H] = entInfo§
% 信息熵函数，P为概率分布，H为该信源的信源熵。如输入P = [1/2, 1/2]
% 则输出为1

根据所编函数计算如下信源的自信息量及信源熵。

2、有条英文信息总共包含100个字符，假定其中每个字符从26个英文字母和3个标点符号中等概率选取，那么这条信息提供的信息量为多少？

3、若将上述29个字符分为三类，第一类中包含9个字符，该类出现的概率为1/7；第二类中包含13个字符，该类出现的概率为2/7；第三类中包含7个字符，该类出现的概率为4/7；每类中各字符均以等概率出现，求此时该信源的信息熵。

4、有两个二元随机变量X和Y，它们的联合概率分布函数如下表：
Y X 0 1
0 1/8 3/8
1 3/8 1/8
条件概率公式： ，试求：
a、熵H(X),联合熵H(X,Y);
b、条件熵H(X|Y);
c、平均互信息I(X;Y);

discretesource1

import numpy as np

def selfinformation(p):
    return  (-1)*np.log2(p)

def inforsouentr(m):
    c = 0
    for i in m:
            c += (i) * selfinformation(i)
    return c

if __name__=='__main__':    
    a = [1/2,1/4,1/4]
    print(inforsouentr(a))

discretesource2

import discretesource1
p = 1/29
#100事件同时出现
print(discretesource1.selfinformation(p)*100)
p  = p**100
print(discretesource1.selfinformation(p))

discretesource3

"""若将上述29个字符分为三类，
第一类中包含9个字符，该类出现的概率为1/7；
第二类中包含13个字符，该类出现的概率为2/7；
第三类中包含7个字符，该类出现的概率为4/7；
每类中各字符均以等概率出现，求此时该信源的信息熵。"""
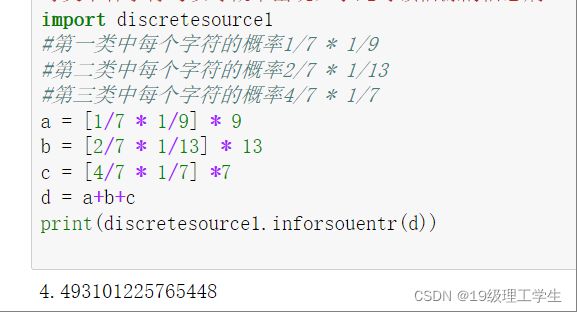
import discretesource1
#第一类中每个字符的概率1/7 * 1/9
#第二类中每个字符的概率2/7 * 1/13
#第三类中每个字符的概率4/7 * 1/7
a = [1/7 * 1/9] * 9
b = [2/7 * 1/13] * 13
c = [4/7 * 1/7] *7
d = a+b+c
print(discretesource1.inforsouentr(d))

discretesource4

# a、熵H(X),联合熵H(X,Y);
# b、条件熵H(X|Y);
# c、平均互信息I(X;Y);
import discretesource1
import numpy as np
p = np.array([[1/8,3/8],[3/8,1/8]])
#按行相加求x概率
x = np.sum(p,axis = 1 )
#按列相加求y概率
y = np.sum(p,axis = 0 )
#熵H(X)
print("熵H(X)",discretesource1.inforsouentr(x))
#联合熵H(X,Y)
print("联合熵H(X,Y)",discretesource1.inforsouentr(p.flatten()))
# #b、条件熵H(X|Y);
a = np.divide(p,y)
c= 0
c = p * discretesource1.selfinformation(a)
c = np.sum (c.flatten())
print("条件熵H(X|Y)",c)
#c、平均互信息I(X;Y)
b = np.divide(a,x.reshape(2,1))
c = p * np.log2(b)
c = np.sum (c.flatten())

print("平均互信息I(X;Y)",c)