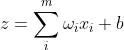深度学习中各种神经网络小结（感知机、神经网络CNN/RNN、激活函数、过拟合）
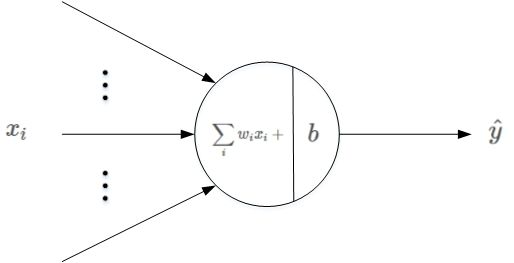
感知机
多个输入，只有一个输出
输入和输出间学习一个线性关系
增加一个激活函数（符号函数）
得到一个二分类输出结果1或-1
模型局限性：仅用于二分类模型，无法学习更复杂的非线性模型，因此工业界无法应用
神经网络
对感知机做了改进和扩展：
1、加入隐藏层，隐藏层可以是多层或单层，层数越多，模型表达能力越强，复杂度也越高
2、多个输出，可用于分类回归、降维聚类
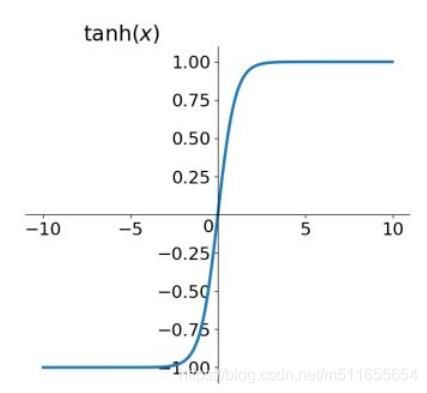
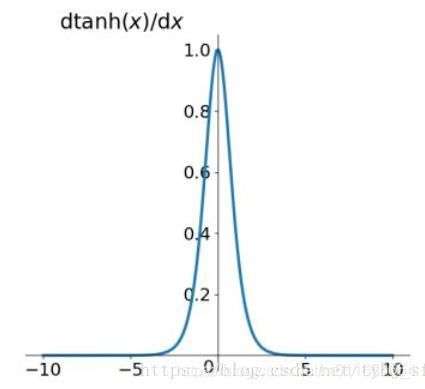
3、激活函数可选择性变高（激活函数是非线性函数，不是用激活函数相当于f(z)=z，无论隐藏层多少，输出是输出的线性组合，与没有隐藏层相当，就是原始感知机，网络逼近能力有限）
| 函数 | 公式 | 几何图形 | 优点 | 缺点 | 应用场景 | |
| sigmoid 函数 |
|
f(z)
df(z)/dz
|
把输入的连续实值变换为0和1之间的输出 | （1）在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大 （2）Sigmoid 的 output 不是0均值（即zero-centered） （3）其解析式中含有幂运算，计算机求解时相对来讲比较耗时 |
目前不常使用，最好不要使用（在逻辑回归中使用） | |
| tanh 函数 |
 |
tanh(x)
dtanh(x)/dx
|
解决了Sigmoid函数的不是zero-centered输出问题 | 梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在 | 一般效果比不上Relu和maxout | |
| ReLu 函数 |
 |
Relu(x)
dRelu(x)/dx |
(1） 解决了gradient vanishing问题 (在正区间) (2）计算速度非常快，只需要判断输入是否大于0 (3）收敛速度远快于sigmoid和tanh |
（1）ReLU的输出不是zero-centered |
并不是全区间可导的，但最常用，建模时推荐优先尝试，relu还有各种改造形式 | |
| MaxOut 函数 |
|
k是maxout层所需要的参数，人工设定，权重w是一个大小为(d,m,k)三维矩阵，b是一个大小为(m,k)的二维矩阵，这两个就是需要学习的参数 | ||||
| softmax 函数 |
|
 |
多分类神经网络输出，输出神经元在[0,1]之间，输出之和为1 |
![h_{i}(x)=\underset{j\in [1,k]}{max}z_{ij}](http://img.e-com-net.com/image/info8/b2e2efb4dbb34a6685b437428ac5ed51.gif){kind=small}
深度神经网络DNN
深度神经网络，也叫多层神经网络或多层感知机（Multi-Layer perceptron, MLP），神经网络层有三种类型：输入层（第一层）、隐藏层（中间层）、输出层（最后一层）。层与层之间的神经元是全连接的，
前向传播：
利用上一层的输出作为下一层的输入，增加权重系数W和偏置b，再计算下一层的输出。
反向传播：
目的：
找到合适的所有隐藏层和输出层对应的线性系数矩阵W,偏置向量b,让所有的训练样本输入计算出的输出尽可能的等于或很接近样本输出。
具体步骤：
选择一个合适的损失函数度量训练样本的输出损失，再进一步最小化损失函数求极值进行优化，最终求得最优W和b。
通常损失函数优化极值求解采用梯度下降法迭代完成，也可用牛顿法、拟牛顿法。
卷积神经网络CNN
卷积神经网络，有输入层、输出层、隐藏层组成，隐藏层包括卷积层、relu层、池化层、全连接层。常见CNN结构
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC
堆叠几个卷积和整流层，再加一个池化层，重复这个模式知道图片已经被合并得比较小了，然后再用全连接层控制输出。
输入层：
可以是图像的二维向量，或者带有RGB通道（高度）的三维向量，也可以是文本的一维向量，做卷积操作时只向下滑动窗口，只左右滑动。
隐藏层：
卷积层（Convolutional layer）
设置一定尺寸F*F的滤波器（filter），先确定是否对原始数据m*n补零（zero-padding)操作（补零可以改变输入的大小，一般是为了第一步卷积前保留原始图像的边缘信息），再对原始数据采用一定的步长（stride）进行卷积（窗口滑动），计算每一次滑动是卷积的结果（输入和滤波器的点积），产生新的输出结果。这个输出是对输入做筛选，提取更高层次的特征（特征与滤波器结构类似，其他的则过滤掉）。卷积结果输出大小
，若结果
- W : 输入单元的大小（长m或宽n）
- F : 滤波器尺寸大小
- S : 步幅（stride）
- P : 补零（zero-padding)的数量
- K : 深度，输出单元的深度
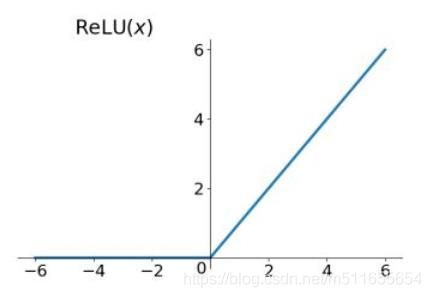
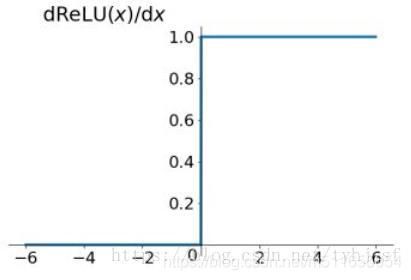
线性整流层（Rectified Linear Units layer, ReLU layer）
设置一定的激活函数，对卷积层输出做线性变换或非线性变换。
池化层（Pooling layer）
池化层，也称下采样，通常卷积层得到的特征维度很大，池化目的是保留数据主要信息，剔除噪音，减小数据维度。常用最大池化max pooling、均值池化mean pooling。
全连接层（ Fully-Connected layer）
把所有局部特征结合变成全局特征，用来计算每一类的得分概率分布。
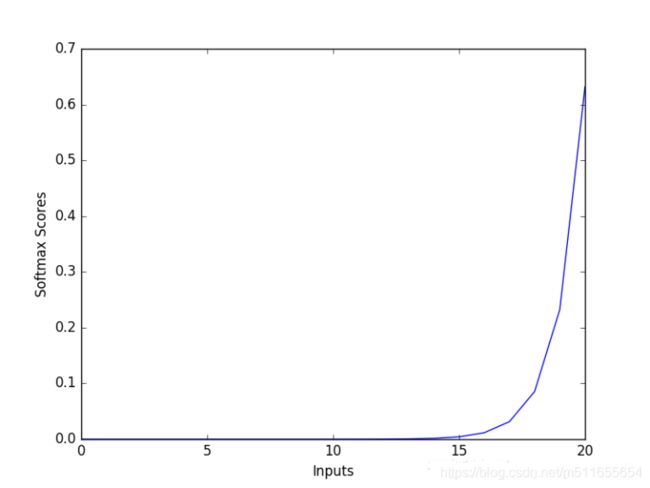
输出层：
对结果的预测值，一般会加一个softmax层。
CNN特点
局部感知
卷积核和图像卷积的时候，每次卷积核所覆盖的像素只是一小部分，是局部特征。最后从局部到整体（全连接层）。而传统神经网络是整体感知。
权重共享
CNN除全连接层外，卷积层参数完全取决于滤波器尺寸大小和个数。与传统的神经网络相比，参数量小，计算量小。整个图片共享一组滤波器的参数。
多卷积核
一种卷积核代表的是一种特征，为获得更多不同的特征集合，卷积层会有多个卷积核，生成不同的特征，这也是为什么卷积后的图片的高，每一个图片代表不同的特征。
过拟合解决方法
过拟合：神经网络的神经元过多，参数过多，导致训练集拟合得太好了，泛化性能差
- L2正则化
- dropout：丢弃一些神经元
在每个隐藏层的输入进行一个概率判决，比如我们设置概率为0.5（通常命名为keep_prob）,根据0.5，我们生成一个跟隐藏层神经元个数的向量，true:false的比例是1：1（因为keep_prob=0.5），与隐藏层的输入进行相乘，那么会有一半隐藏层的神经元被丢掉，不起作用，整个网络变得简单了，就会从过拟合过渡到just right 。
- shuffle：每个epoch之后shuffle训练数据，设置early-stopping
- Batch Normalization
BN首先是把所有的samples的统计分布标准化，降低了batch内不同样本的差异性，然后又允许batch内的各个samples有各自的统计分布，BN最大的优点为允许网络使用较大的学习速率进行训练，加快网络的训练速度（减少epoch次数），提升效果。
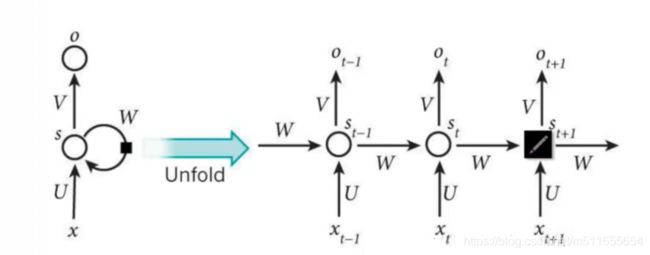
循环神经网络RNN
无论是深度神经网络还是卷积神经网络，元素之间相互独立，输入和输出也是独立的。但有些场景元素会随时间变化，或者有因果关系、有相互联系等，所以RNN出现了，像人一样拥有记忆，输出依赖于当前输入和历史记忆。
参考文献
- 深度神经网络（DNN）模型与前向传播算法
- 深度神经网络（DNN）反向传播算法(BP)
- 常用激活函数（激励函数）理解与总结
- CNN初探
- 详解卷积神经网络(CNN)
- 面试常问的深度学习(DNN、CNN、RNN)的相关问题
- 技术向：一文读懂卷积神经网络CNN
- 循环神经网络（RNN）原理通俗解释