Pytorch nn.Linear的基本用法

nn.Linear的基本定义

nn.Linear定义一个神经网络的线性层，方法签名如下：

torch.nn.Linear(in_features, # 输入的神经元个数
           out_features, # 输出神经元个数
           bias=True # 是否包含偏置
           )

Linear其实就是对输入 $X_{n\times i}$ 执行了一个线性变换，即：

$$Y_{n\times o}=X_{n\times i}{W}_{i\times o}+b$$

其中$W$是模型要学习的参数，$W$ 的维度为 $W_{i\times o}$ , $b$ 是o维的向量偏置，$n$ 为输入向量的行数（例如，你想一次输入10个样本，即batch_size为10，则$n=10$ ），$i$ 为输入神经元的个数（例如你的样本特征数为5，则 $i=5$ ），$o$ 为输出神经元的个数。

使用演示：

from torch import nn
import torch

model = nn.Linear(2, 1) # 输入特征数为2，输出特征数为1

input = torch.Tensor([1, 2]) # 给一个样本，该样本有2个特征（这两个特征的值分别为1和2）
output = model(input)
output

tensor([-1.4166], grad_fn=)

我们的输入为[1,2]，输出了[-1.4166]。可以查看模型参数验证一下上述的式子：

# 查看模型参数
for param in model.parameters():
    print(param)

Parameter containing:
tensor([[ 0.1098, -0.5404]], requires_grad=True)
Parameter containing:
tensor([-0.4456], requires_grad=True)

可以看到，模型有3个参数，分别为两个权重和一个偏执。计算可得：

$$y=[1,2]\ast [0.1098,-0.5404{]}^T-0.4456=-1.4166$$

实战

假设我们的一次输入三个样本A,B,C（即batch_size为3），每个样本的特征数量为5：

A: [0.1,0.2,0.3,0.3,0.3]
B: [0.4,0.5,0.6,0.6,0.6]
C: [0.7,0.8,0.9,0.9,0.9]

则我们的输入向量 $X_{3\times 5}$ 为：

X = torch.Tensor([
    [0.1,0.2,0.3,0.3,0.3],
    [0.4,0.5,0.6,0.6,0.6],
    [0.7,0.8,0.9,0.9,0.9],
])
X

tensor([[0.1000, 0.2000, 0.3000, 0.3000, 0.3000],
        [0.4000, 0.5000, 0.6000, 0.6000, 0.6000],
        [0.7000, 0.8000, 0.9000, 0.9000, 0.9000]])

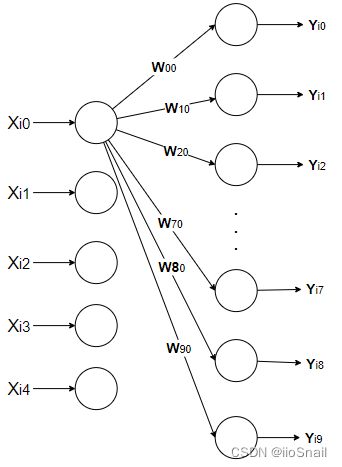
定义线性层，我们的输入特征为5，所以in_feature=5，我们想让下一层的神经元个数为10，所以out_feature=10，则模型参数为：$W_{5\times 10}$

model = nn.Linear(in_features=5, out_features=10, bias=True)

经过线性层，其实就是做了一件事，即：$$Y_{3\times 10}=X_{3\times 5}{W}_{5\times 10}+b$$

具体表示则为：
$$\left[\begin{array}{ccccc}{Y}_{00}& Y_{01}& \cdots & Y_{08}& Y_{09}\\ Y_{10}& Y_{11}& \cdots & Y_{18}& Y_{19}\\ Y_{20}& Y_{21}& \cdots & Y_{28}& Y_{29}\end{array}\right]=\left[\begin{array}{ccccc}{X}_{00}& X_{01}& X_{02}& X_{03}& X_{04}\\ X_{10}& X_{11}& X_{12}& X_{13}& X_{14}\\ X_{20}& X_{21}& X_{22}& X_{23}& X_{24}\end{array}\right]\left[\begin{array}{ccccc}{W}_{00}& W_{01}& \cdots & W_{08}& W_{09}\\ W_{10}& W_{11}& \cdots & W_{18}& W_{19}\\ W_{20}& W_{21}& \cdots & W_{28}& W_{29}\\ W_{30}& W_{31}& \cdots & W_{38}& W_{39}\\ W_{40}& W_{41}& \cdots & W_{48}& W_{49}\end{array}\right]+b$$

其中 $X_{i\cdot }$就表示第$i$个样本，$W_{\cdot j}$ 表示所有输入神经元到第$j$个输出神经元的权重。

注意：这里图有点问题，应该是$W_{00},W_{01},W_{02},...,W_{07},W_{08},W_{09}$

因为有三个样本，所以相当于依次进行了三次 $Y_{1\times 10}=X_{1\times 5}{W}_{5\times 10}$，然后再将三个 $Y_{1\times 10}$ 叠在一起

经过线性层后，我们最终的到了$3\times 10$维的矩阵，即 输入3个样本，每个样本维度为5，输出为3个样本，将每个样本扩展成了10维

model(X).size()

torch.Size([3, 10])

---

参考资料

nn.Linear官方文档：https://pytorch.org/docs/stable/generated/torch.nn.Linear.html