基于Labview的图像傅里叶变换研究-含Labview程序
⭕⭕ 目 录 ⭕⭕
- ✳️ 一、傅里叶(Fourier)分析基本理论
-
- ✳️ 1.1 时域与频域
- ✳️ 1.2 傅里叶级数(Fourier Series)与傅里叶变换(Fourier Transformation)
- ✳️ 二、基于Labview的图像傅里叶变换研究
- ✳️ 三、Labview程序获取
✳️ 一、傅里叶(Fourier)分析基本理论
法国数学家傅里叶(Fourier) 于 1807 年受到热传导理论的启示, 首先提出傅里叶(Fourier)分析,傅里叶(Fourier)分析是小波分析的基础。
✳️ 1.1 时域与频域
时域分析就是以时间作为参照来观察动态世界变化的方法,如春夏秋冬四季更迭,人的外表随着时间的变化而变化,股票的价格随着时间的变化而变化,似乎生活的一切都会随着时间的变化而变化,并且我们发现这种变化是永远存在的,时间是不会静止。
频域分析就是换另一种方法来观察我们的世界,认为整个世界其实是静止不变的, 这个静止的世界就叫做频域。 这个理论似乎与客观世界相悖,但通过举例就可以发现它的奥妙之处:
例如一段音乐,音乐用时域的眼光来看就是一个随着时间变化的震动,见图1:
而对于演奏的乐手来说,乐谱是以音符的形式记录的,如下图2:
两张图结合对比,我们发现同样的一段音乐旋律,可以用看似嘈杂烦乱,变化无常的时域图表示,也可以用一个个静止的音符联合而成的有规律的频域图所代替。
看世界的眼光从时域转向了频域就是傅里叶(Fourier) 分析。 傅里叶分析的核心思想就是变换和分解, 从数学的角度上说, 首先是将原周期函数分解,然后再将分解的周期函数变换成各种频率函数的叠加,从而更加准确地理解和把握原周期函数的内涵和精髓。 也就是说任何周期函数都可以看作是不同振幅,不同相位正弦波的叠加。
✳️ 1.2 傅里叶级数(Fourier Series)与傅里叶变换(Fourier Transformation)
傅里叶级数又叫三角级数,简单地说就是把一个函数 Y 拆成若干三角函数的和。
这个公式的含义就是正弦函数和余弦函数以某种方式叠加可以等于一个周期函数。也就是说信号函数可以用正弦函数和余弦函数组合替代。用画图来表示就是一条看似很不规则的多弯曲的周期曲线,也可以用许许多多的规整的光滑曲线组合而成, 这就是傅里叶变换的思路。 如图3。
傅里叶变换的定义:若给定信号 f(t) 满足绝对可积条件,其标准傅里叶(Fourier)变换为:
所谓傅里叶变换就是通过时频信号之间的相互转换, 把在时域领域中无法解决的问题拿到频域中去解决, 将较为复杂的事件计算转变为计算简单的影射事件,计算的结果又还原回去,和原函数的计算结果是一样的。傅里叶分析是数学领域上的又一进步,使很多原本不好解决的数学难题,如复杂的微分方程可以很容易用傅里叶求解。正是有了傅里叶的思想和分析方法,才有了后来计算机, CD, 电话,收音机, X 射线等等的新式电器设备的发明产生,所以后来的物理学家麦克斯韦尔(James Clark Maxwell)称傅里叶分析时数学史上一部伟大的史诗。
✳️ 二、基于Labview的图像傅里叶变换研究
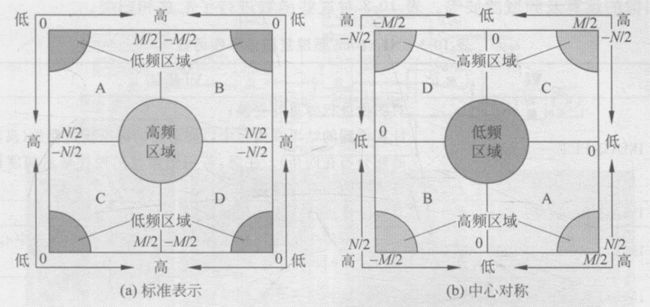
一般来说,对数字图像进行傅里叶变换后,所得到频谱图像的原点位于图像的左上角,这种表示方式称为标准表示模式( standard representation)。标准表示模式下,高频分量集中在频谱图的中心区域,而低频分量则集中在频谱图的四角,频率为0的部分(直流成分)则集中位于频谱图的左上角,整个图像显示一个完整周期[-M/2,M/2]×[-N/2,N/2]内的频谱。
另一种常见的图像频谱表示方式为中心对称( central symmetric representation)或类光(optical representation)表示模式。中心对称表示模式下,低频分量集中在频谱图的中心区域,而高频分量则集中在频谱图的四角,频率为0的部分(直流成分)则集中位于频谱图的中心(M/2,N/2)处,整个图像显示一个完整周期[-M/2,M/2]×[-N/2,N/2]内的频谱。图4显示了两种图像频谱表示方式的示意图,可以看出两种显示方式可以通过调换4个小矩形的区域来相互转换。
基于Labview实现的图像傅里叶变换结果如下图所示:
图6显示了对一幅图像及其旋转45°后分别进行FFT的实例。程序先将图像读入内存,并使用 IMAQ Rotate将其逆时针旋转45°。由于需要显示旋转前后的图像,因此读入和旋转图像时,均指定图像格式为RGB(U32)。此后,程序分别对原图和旋转后的图像进行傅里叶变换,并以中心对称模式显示变换后图像的频谱。由于傅里叶变换过程需要进行复数运算,因此在变换前需要先用 IMAQ Cast Image将图像格式由RGB转换为复图像。经傅里叶变换得到图像的频谱后,程序释放所有缓冲区并结束运行。
✳️ 三、Labview程序获取
上述演示的Labview程序,可私信博主获取(订阅该专栏获取该程序一份:基于Labview的图像傅里叶变换研究-含Labview程序):
博主简介:研究方向涉及智能图像处理、深度学习等领域,先后发表过多篇SCI论文,在科研方面经验丰富。任何与算法、程序、科研方面的问题,均可私信交流讨论。