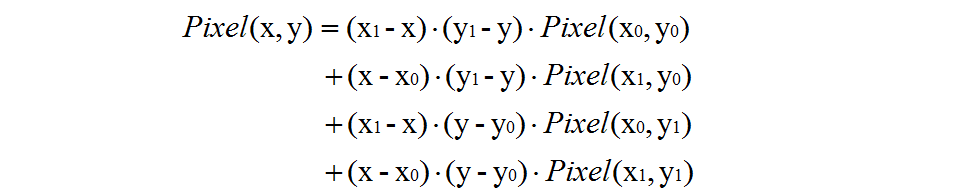更灵活、有个性的卷积——可变形卷积（Deformable Conv）

 

作者简介

CW，广东深圳人，毕业于中山大学（SYSU）数据科学与计算机学院，毕业后就业于腾讯计算机系统有限公司技术工程与事业群（TEG）从事Devops工作，期间在AI LAB实习过，实操过道路交通元素与医疗病例图像分割、视频实时人脸检测与表情识别、OCR等项目。

目前也有在一些自媒体平台上参与外包项目的研发工作，项目专注于CV领域（传统图像处理与深度学习方向均有）。

 

 

前言

相信大家在看paper的时候或多或少都能见到Deformable操作的身影，这种可变形操作可嵌入到算法中的许多部分，最常见的是可变形卷积，另外还有对候选区域的池化等，它们都是从 Deformable Convolutional Networks(DCN) 中衍生出来的。

作者将DCN中有关可变形卷积的知识梳理了一番，同时基于Pytorch框架进行源码实现，在加深理解的同时还可方便自己日后使用，感兴趣的朋友们也可以共同享用，我不独食，一起嚼，更香！

  

 

本文概述

I. Deformable Conv：我是个会变形（不是变性哦）的个性boy

II. 揭秘可变形卷积大法

III. 还没吃饱？这就来解析源码！

  

 

Deformable Conv：我是个会变形的个性boy

传统的卷积操作是将特征图分成一个个与卷积核大小相同的部分，然后进行卷积操作，每部分在特征图上的位置都是固定的。这样，对于形变比较复杂的物体，使用这种卷积的效果就可能不太好了。

对于这种情况，传统做法有丰富数据集，引入更多复杂形变的样本、使用各种数据增强和trick，以及人工设计一些手工特征和算法。

基于数据集和数据增强的做法都有点“暴力”，通常收敛慢而且需要较复杂的网络结构来配合；而基于手工特征算法就实在是有点“太难了”。特变是物体形变可能千变万化，这种做法本身难度就很大，而且不灵活，炼丹本身就够辛苦了，何必这么折腾呢？

这时候，Deformable Conv 出道了！他站上演讲台，说他是个性boy，他会变形，不像常规卷积那样死板，他更灵活，可以应对上述提到的物体复杂形变的场景。

那 Deformable Conv 是怎么解决问题的呢？

Deformable Conv 在感受野中引入了偏移量，而且这偏移量是可学习的，我这招可以使得感受野不再是死板的方形，而是与物体的实际形状贴近，这样之后的卷积区域便始终覆盖在物体形状周围，无论物体如何形变，我加入可学习的偏移量后通通搞定！” 话音刚落，他还顺带秀出了他这招的效果：

可变形卷积 vs 标准卷积

上图(a)中绿色的点代表原始感受野范围，(b)、(c)和(d)中的蓝色点代表加上偏移量后新的感受野位置，可以看到添加偏移量后可以应对诸如目标移动、尺寸缩放、旋转等各种情况。

 

 

揭秘可变形卷积大法

Deformable conv 一直遵奉开源协同，共同学习，共同进步，大家好才是真的好，世界才美好！下面他就为大家揭秘了他的大招——可变形卷积大法。

传统的卷积结构可以定义成公式1，其中是输出特征图的每个点，与卷积核中心点对应，pn是p0在卷积核范围内的每个偏移量。

 常规卷积公式

而可变形卷积则在上述公式1的基础上为每个点引入了一个偏移量，偏移量是由输入特征图与另一个卷积生成的，通常是小数。

可变形卷积公式

 

由于加入偏移量后的位置非整数，并不对应feature map上实际存在的像素点，因此需要使用插值来得到偏移后的像素值，通常可采用双线性插值，用公式表示如下：

双线性插值公式

上述公式的意义就是说将插值点位置的像素值设为其4领域像素点的加权和，领域4个点是离其最近的在特征图上实际存在的像素点，每个点的权重则根据它与插值点横、纵坐标的距离来设置，公式最后一行的max(0, 1-...)就是限制了插值点与领域点不会超过1个像素的距离。

可变形卷积示意图

Deformable Conv boy给出了可变形卷积操作的简单示意图，可以看到offsets是额外使用一个卷积来生成的，与最终要做卷积操作那个卷积不是同一个。

 

 

源码解析

毕竟炼丹本来就够玄的了，叙述完原理后，如果没有实实在在的代码，那就如同痴人说梦话！Deformable Conv boy不愧是大度的boy，他二话不说，立刻就对他的大招进行源码解析。

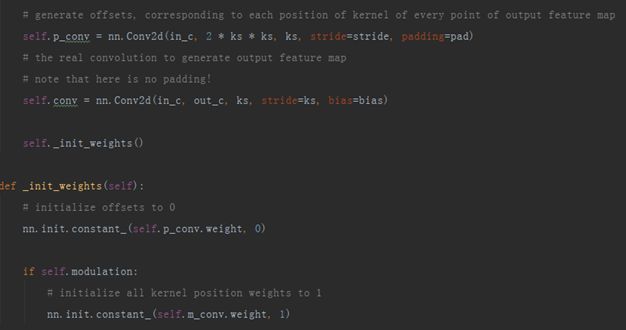
常规操作，他使用nn.Module的子类来封装可变形卷积操作，其中modulation是可选参数，若设置为True，那么在进行卷积操作时，对应卷积核的每个位置都会分配一个权重。

Deformable Conv 源码(i)

p_conv是生成offsets所使用的卷积，输出通道数为卷积核尺寸的平方的2倍，代表对应卷积核每个位置横纵坐标都有偏移量，因此需要乘2。

conv则是最终实际要进行的卷积操作，注意这里步长设置为卷积核大小，因为与该卷积核进行卷积操作的特征图是由输出特征图中每个点扩展为其对应卷积核那么多个点后生成的。

比如conv是3x3卷积，输出特征图尺寸2x3（hxw），那么其每个点都被扩展为9（3x3）个点，对应卷积核的每个位置。于是与conv进行卷积的特征图尺寸变为(2x3) x (3x3)，将stride设置为3，最终输出的特征图尺寸就刚好是2x3。

Deformable Conv 源码(ii)

以上还对p_conv和m_conv的权重进行了初始化。p_conv的权重初始化为0，代表初始时没有偏移量；m_conv的权重初始化为1，代表初始时卷积核每个位置的权重都为1。

下图这部分对应的就是上一节讲到的可变形卷积公式 ，即输出特征图上每点（对应卷积核中心）加上其对应卷积核每个位置的相对（横、纵）坐标后再加上自学习的（横、纵坐标）偏移量。

p0就是将输出特征图每点对应到卷积核中心，然后映射到输入特征图中的位置；pn则是p0对应卷积核每个位置的相对坐标。

比如使用3x3卷积，那么对于卷积核的1个中心点来说，在pn中，横、纵相对坐标各3个值（-1、0、1），组合起来一共有9（3x3）个值，pn仅与卷积核尺寸相关。p0、pn、offset的形状都是一样的，其中N为卷积核尺寸的平方（如果是3x3卷积的话，N就是9）。

Deformable Conv 源码(iii)

接下来解析p0的计算，p0_y、p0_x就是输出特征图每点映射到输入特征图上的纵、横坐标值。根据torch.arange()那部分可知，纵、横坐标分别都有out_h和out_w个，与输出特征图尺寸对应。

kc是卷积核中心位置，比如3x3卷积的话，中心点位置就是（1,1），然后根据卷积的步长和输出特征图尺寸就能得到在每个卷积过程中，中心点对应在输入特征图上的位置。

最后，这里将p0_y和p0_x进行reshape是为了在后续操作时和pn以及offset的形状对应上。

Deformable Conv 源码(iv)

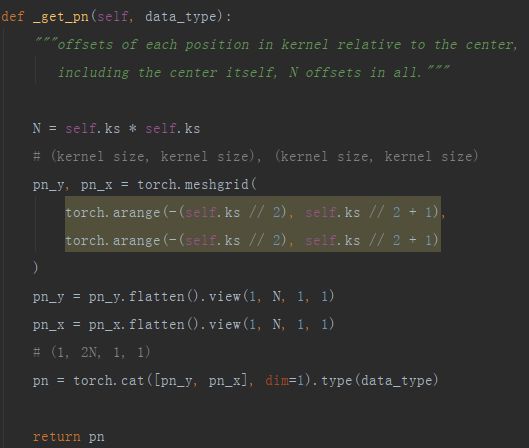
搞定完p0，接下来撸一撸pn。与p0的计算类似，只不过其仅由卷积核尺寸决定，由于卷积核中心点位置是其尺寸的一半，于是中心点向左（上）方向移动尺寸的一半就得到起始点，向右（下）方向移动另一半就得到终止点，这就是以下torch.arange()部分对应的内容。

Deformable Conv 源码(v)

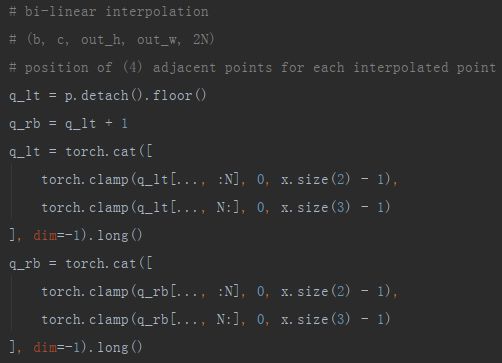
OK，至此我们得到了卷积时每点偏移后的位置，但是如上一节所述，这些位置通常是小数，并不对应特征图上实际的像素点，Deformable Conv boy 使用双线性插值来计算这些位置的像素值，使用这招首先需要知道每个位置点最近的4领域点，它们是特征图上实际的像素点，再根据4领域点与插值点位置的距离设置权重，最终由这些权重和像素值进行加权求和得到插值点的像素。

以下就是得到4领域点位置的计算过程，同时需要注意将这些位置限制在输入特征图尺寸范围内。

Deformable Conv 源码(vi)

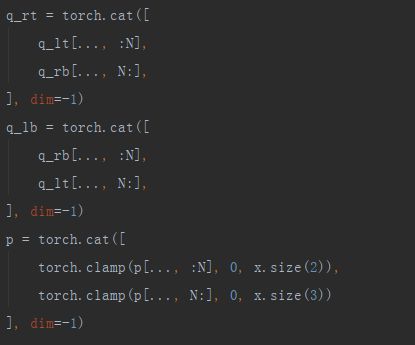
Deformable Conv 源码(vii)

计算出4领域点的位置后，理所当然地，我们需要知道它们的像素值，下图中由_get_x_q()这个方法得到。另外，g_xx部分计算的是4领域点对应的权重。

Deformable Conv 源码(viii)

最后，将4领域点的权重和像素值进行加权求和得到插值点像素值。

Deformable Conv 源码(ix)

以上双线性插值的计算过程可结合下面几张图来理解。

双线性插值示意图(i)

双线性插值示意图(ii)

由于领域间像素点的横、纵坐标之差都是1，于是可以简化为下面的公式。

双线性插值示意图(iii)

搞定这部分，我们已经可以得到偏移后位置的像素值了，但是还没有解释如何得到4领域点的像素值，现在就来一探究竟。

q是领域点在输入特征图上的位置，其最后一维2N的前半部分代表纵坐标，后半部分代表横坐标，将输入特征图x进行reshape后，最后一维是高和宽的乘积，于是q[.., :N] * in_w + q[..., N:]就是为了和x的位置对应上。

最后使用Pytorch内置的gather方法，将对应位置的张量值取出。

Deformable Conv 源码(x)

知道了如何得到领域点的像素值，之前的困惑也即烟消云散，我们终于可以进行真正的卷积操作了！也不容易呐~

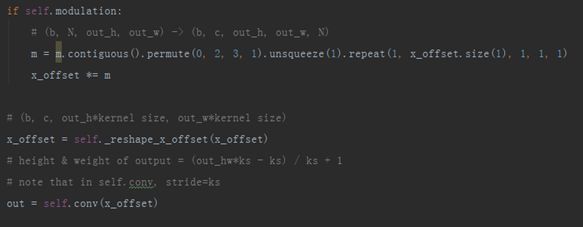
首先，如果设置了modulation，那么就对每个位置乘上其对应的权重，在这之前注意要将权重m的形状变为和x_offset一致。然后需要对x_offset也进行reshape操作，在这一节开头时谈到self.conv的步长设置时就提到了，最终进行卷积时特征图的尺寸宽、高是输出特征图宽、高的卷积核尺寸倍数，结合卷积核大小及步长（同样为卷积核尺寸），最终输出的特征图尺寸便刚刚好。

Deformable Conv 源码(xi)

Deformable Conv boy 也是够“尽心尽力”，连最后一点私藏都要揭秘，他还秀出是如何对x_offset进行reshape的。

Deformable Conv 源码(xii)

但是他不再多言，最后这部分留给大家细细品味，他已算是“仁至义尽”了，台下众人也都服了，在心里传送出“6666666...”电波。

 

 

 

总结

每当写文章涉及到源码解析的内容时我都觉得真心不容易，有些代码的实现很难用文字去叙述明白（所谓“道可道，非常道”..），几乎每句话我都会斟酌好几番才输出，写完后也会反复阅读是否有不妥，我要求自己在保证准确性的同时能叙述得简单易懂。另外，为了避免文章读起来晦涩无趣，我有时也会使用些网络词语营造一个轻松活跃的气氛。

尽管代码解析的内容读起来可能有点绕，但我始终偏向于在文章中将这部分内容囊括进来，因为只讲原理实在太空洞，只有结合了代码进行实践，才是把算法知识落实了下去。

如果各位对文中内容有疑惑或者发现文中内容有误，请积极反馈，谢谢！