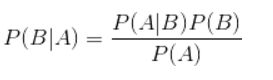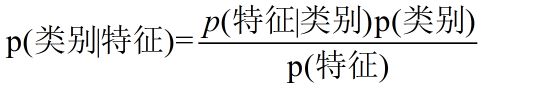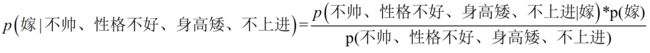朴素贝叶斯算法(1)
1.1 朴素贝叶斯简述
朴素贝叶斯算法(Naive Bayes, NB) 是应用最为广泛的分类算法之一。既可以用于二分类,也可以用于多分类。当年的垃圾邮件分类都是基于朴素贝叶斯分类器识别的。
朴素贝叶斯假设(又叫条件独立性假设):即,在给定y的条件下,属性之间相互独立。
假设目的:简化运算。
虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。
1.2 概率基础复习
1.概率定义
- 概率定义为一件事情发生的可能性
- 扔出一个硬币,结果头像朝上
- P(X) : 取值在[0, 1]
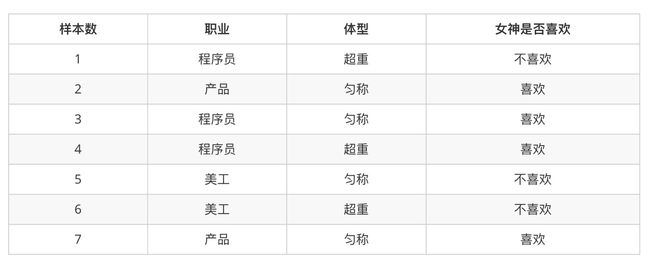
2.案例:判断女神对你的喜欢情况
在讲这两个概率之前我们通过一个例子,来计算一些结果:
问题如下:
- 女神喜欢的概率?
- 职业是程序员并且体型匀称的概率?
- 在女神喜欢的条件下,职业是程序员的概率?
- 在女神喜欢的条件下,职业是程序员、体重超重的概率?
计算结果为:
P(喜欢) = 4/7
P(程序员, 匀称) = 1/7(联合概率)
P(程序员|喜欢) = 2/4 = 1/2(条件概率)
P(程序员, 超重|喜欢) = 1/4
3.联合概率、条件概率与相互独立
- 联合概率:包含多个条件,且所有条件同时成立的概率
- 记作:P(A,B)
- 条件概率:就是事件A在另外一个事件B已经发生条件下的发生概率
- 记作:P(A|B)
- 相互独立:如果P(A, B) = P(A)P(B),则称事件A与事件B相互独立。
4.贝叶斯公式
4.1 公式介绍
换个表达形式就会明朗很多,如下:
我们最终求的p(类别|特征)即可!就相当于完成了我们的任务。
根据朴素贝叶斯假设:p(特征/类别) = p(特征1/类别)* p(特征2/类别)… *p(特征n/类别)
4.2 例题分析
下面我先给出例子问题。
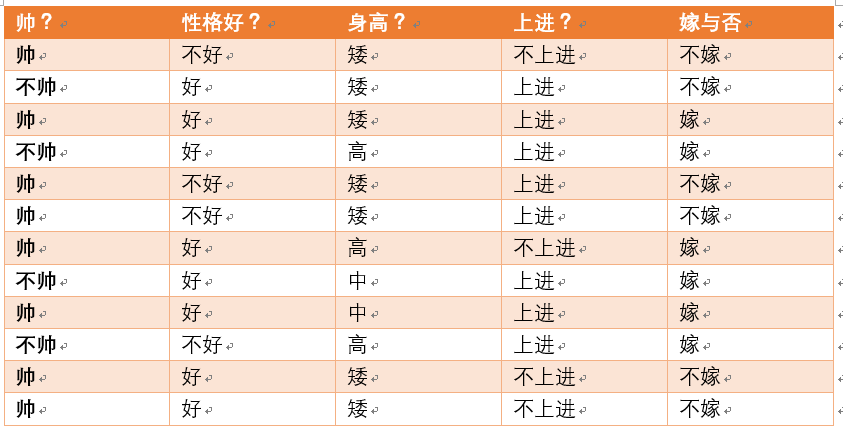
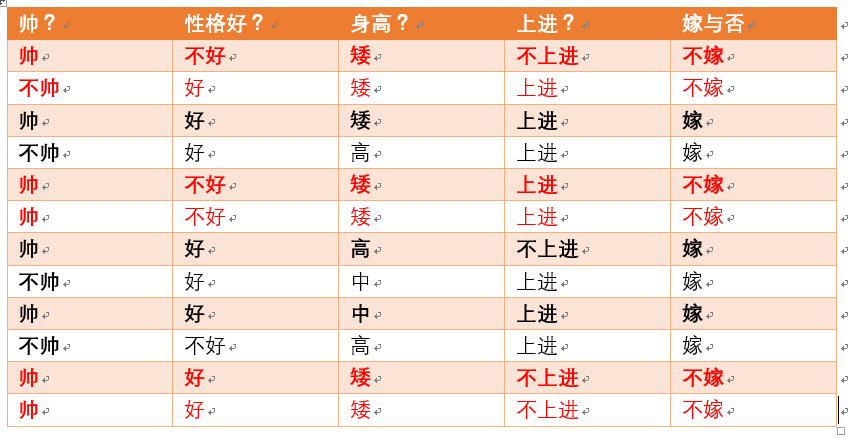
给定数据如下:
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
这里我们联系到朴素贝叶斯公式:
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
嫁的概率为:
p ( 嫁 / 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) = p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 / 嫁 ) ∗ p ( 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) p(嫁/不帅、性格不好、身高矮、不上进)=\frac {p(不帅、性格不好、身高矮、不上进/嫁)*p(嫁)}{p(不帅、性格不好、身高矮、不上进)} p(嫁/不帅、性格不好、身高矮、不上进)=p(不帅、性格不好、身高矮、不上进)p(不帅、性格不好、身高矮、不上进/嫁)∗p(嫁)
= p ( 不 帅 / 嫁 ) p ( 性 格 不 好 / 嫁 ) p ( 身 高 矮 / 嫁 ) p ( 不 上 进 / 嫁 ) ∗ p ( 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) \frac {p(不帅/嫁)p(性格不好/嫁)p(身高矮/嫁)p(不上进/嫁)*p(嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不帅、性格不好、身高矮、不上进)p(不帅/嫁)p(性格不好/嫁)p(身高矮/嫁)p(不上进/嫁)∗p(嫁)
不嫁的概率为:
p ( 不 嫁 / 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) = p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 / 不 嫁 ) ∗ p ( 不 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) p(不嫁/不帅、性格不好、身高矮、不上进)=\frac {p(不帅、性格不好、身高矮、不上进/不嫁)*p(不嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不嫁/不帅、性格不好、身高矮、不上进)=p(不帅、性格不好、身高矮、不上进)p(不帅、性格不好、身高矮、不上进/不嫁)∗p(不嫁)
= p ( 不 帅 / 不 嫁 ) p ( 性 格 不 好 / 不 嫁 ) p ( 身 高 矮 / 不 嫁 ) p ( 不 上 进 / 不 嫁 ) ∗ p ( 不 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) \frac {p(不帅/不嫁)p(性格不好/不嫁)p(身高矮/不嫁)p(不上进/不嫁)*p(不嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不帅、性格不好、身高矮、不上进)p(不帅/不嫁)p(性格不好/不嫁)p(身高矮/不嫁)p(不上进/不嫁)∗p(不嫁)
我们发现分母相同:p(嫁)>p(不嫁),只需要分子大于就行
朴素贝叶斯算法的朴素一词解释
那么这三个量是如何求得?
是根据已知训练数据统计得来,下面详细给出该例子的求解过程。
回忆一下我们要求的公式如下:
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
我们将上面公式整理一下如下:
p ( 嫁 / 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) = p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 / 嫁 ) ∗ p ( 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) p(嫁/不帅、性格不好、身高矮、不上进)=\frac {p(不帅、性格不好、身高矮、不上进/嫁)*p(嫁)}{p(不帅、性格不好、身高矮、不上进)} p(嫁/不帅、性格不好、身高矮、不上进)=p(不帅、性格不好、身高矮、不上进)p(不帅、性格不好、身高矮、不上进/嫁)∗p(嫁)
= p ( 不 帅 / 嫁 ) p ( 性 格 不 好 / 嫁 ) p ( 身 高 矮 / 嫁 ) p ( 不 上 进 / 嫁 ) ∗ p ( 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) \frac {p(不帅/嫁)p(性格不好/嫁)p(身高矮/嫁)p(不上进/嫁)*p(嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不帅、性格不好、身高矮、不上进)p(不帅/嫁)p(性格不好/嫁)p(身高矮/嫁)p(不上进/嫁)∗p(嫁)
下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
p(嫁)=?
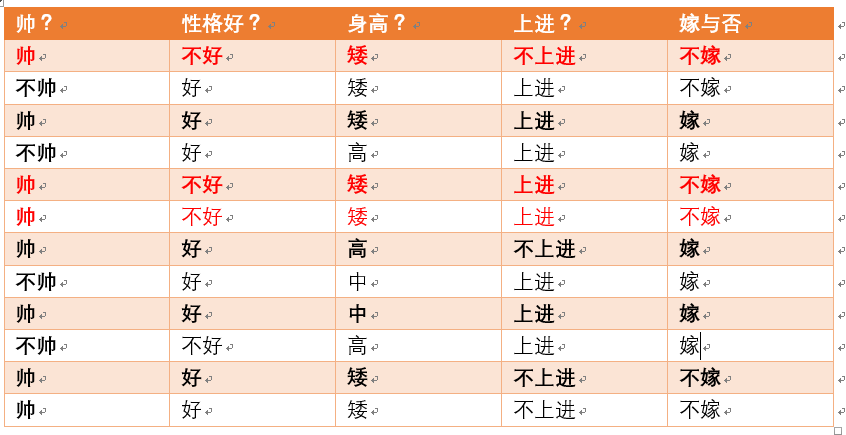
首先我们整理训练数据中,嫁的样本数如下:
则 p(嫁) = 6/12(总样本数) = 1/2
p(不帅|嫁)=?统计满足样本数如下:
则p(不帅|嫁) = 3/6 = 1/2
p(性格不好|嫁)= ?统计满足样本数如下:
**则p(性格不好|嫁)= 1/6
**
p(矮|嫁) = ?统计满足样本数如下:
则p(矮|嫁) = 1/6
p(不上进|嫁) = ?统计满足样本数如下:
则p(不上进|嫁) = 1/6
到这里,要求p(不帅、性格不好、身高矮、不上进|嫁)的所需项全部求出来了,下面我带入进去即可,
p ( 嫁 / 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) = p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 / 嫁 ) ∗ p ( 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) p(嫁/不帅、性格不好、身高矮、不上进)=\frac {p(不帅、性格不好、身高矮、不上进/嫁)*p(嫁)}{p(不帅、性格不好、身高矮、不上进)} p(嫁/不帅、性格不好、身高矮、不上进)=p(不帅、性格不好、身高矮、不上进)p(不帅、性格不好、身高矮、不上进/嫁)∗p(嫁)
= p ( 不 帅 / 嫁 ) p ( 性 格 不 好 / 嫁 ) p ( 身 高 矮 / 嫁 ) p ( 不 上 进 / 嫁 ) ∗ p ( 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) \frac {p(不帅/嫁)p(性格不好/嫁)p(身高矮/嫁)p(不上进/嫁)*p(嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不帅、性格不好、身高矮、不上进)p(不帅/嫁)p(性格不好/嫁)p(身高矮/嫁)p(不上进/嫁)∗p(嫁)
∝p(不帅、性格不好、身高矮、不上进|嫁)*p(嫁)
=p(不帅|嫁)* p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁)*p(嫁)
= 1/2*1/6*1/6*1/6*1/2 = 1/864
下面我们根据同样的方法来求p(不嫁|不帅,性格不好,身高矮,不上进),完全一样的做法,为了方便理解,我这里也走一遍帮助理解。首先公式如下:
p ( 不 嫁 / 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) = p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 / 不 嫁 ) ∗ p ( 不 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) p(不嫁/不帅、性格不好、身高矮、不上进)=\frac {p(不帅、性格不好、身高矮、不上进/不嫁)*p(不嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不嫁/不帅、性格不好、身高矮、不上进)=p(不帅、性格不好、身高矮、不上进)p(不帅、性格不好、身高矮、不上进/不嫁)∗p(不嫁)
= p ( 不 帅 / 不 嫁 ) p ( 性 格 不 好 / 不 嫁 ) p ( 身 高 矮 / 不 嫁 ) p ( 不 上 进 / 不 嫁 ) ∗ p ( 不 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) \frac {p(不帅/不嫁)p(性格不好/不嫁)p(身高矮/不嫁)p(不上进/不嫁)*p(不嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不帅、性格不好、身高矮、不上进)p(不帅/不嫁)p(性格不好/不嫁)p(身高矮/不嫁)p(不上进/不嫁)∗p(不嫁)
下面我也一个一个来进行统计计算
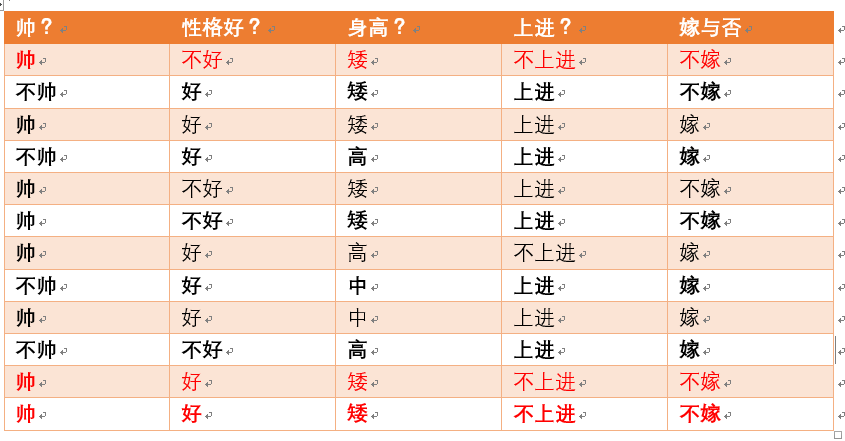
p(不嫁)=?根据统计计算如下(红色为满足条件):
则p(不嫁)=6/12 = 1/2
p(不帅|不嫁) = ?统计满足条件的样本如下(红色为满足条件):
则p(不帅|不嫁) = 1/6
p(性格不好|不嫁) = ?据统计计算如下(红色为满足条件):
则p(性格不好|不嫁) =3/6 = 1/2
p(矮|不嫁) = ?据统计计算如下(红色为满足条件):
则p(矮|不嫁) = 6/6 = 1
p(不上进|不嫁) = ?据统计计算如下(红色为满足条件):
则p(不上进|不嫁) = 3/6 = 1/2
那么根据公式:
p ( 不 嫁 / 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) = p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 / 不 嫁 ) ∗ p ( 不 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) p(不嫁/不帅、性格不好、身高矮、不上进)=\frac {p(不帅、性格不好、身高矮、不上进/不嫁)*p(不嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不嫁/不帅、性格不好、身高矮、不上进)=p(不帅、性格不好、身高矮、不上进)p(不帅、性格不好、身高矮、不上进/不嫁)∗p(不嫁)
= p ( 不 帅 / 不 嫁 ) p ( 性 格 不 好 / 不 嫁 ) p ( 身 高 矮 / 不 嫁 ) p ( 不 上 进 / 不 嫁 ) ∗ p ( 不 嫁 ) p ( 不 帅 、 性 格 不 好 、 身 高 矮 、 不 上 进 ) \frac {p(不帅/不嫁)p(性格不好/不嫁)p(身高矮/不嫁)p(不上进/不嫁)*p(不嫁)}{p(不帅、性格不好、身高矮、不上进)} p(不帅、性格不好、身高矮、不上进)p(不帅/不嫁)p(性格不好/不嫁)p(身高矮/不嫁)p(不上进/不嫁)∗p(不嫁)
∝p(不帅、性格不好、身高矮、不上进|不嫁)*p(不嫁)
=p(不帅|不嫁)* p(性格不好|不嫁)*p(身高矮|不嫁)*p(不上进|不嫁)*p(不嫁)
= 1/6*1/2*1*1/2*1/2 = 1/48
很显然1/48> 1/864
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!!!!
4.3 文章分类计算
需求:通过前四个训练样本(文章),判断第五篇文章,是否属于China类
- 计算结果
P(C|Chinese, Chinese, Chinese, Tokyo, Japan) -->
P(Chinese, Chinese, Chinese, Tokyo, Japan|C) * P(C) / P(Chinese, Chinese, Chinese, Tokyo, Japan)
∝
P(Chinese|C)^3 * P(Tokyo|C) * P(Japan|C) * P(C)
# 分母值都相同不用计算:
# 首先计算是China类的概率:
P(Chinese|C=china) = 5/8
P(Tokyo|C) = 0/8
P(Japan|C) = 0/8
# 接着计算不是China类的概率:
P(Chinese|C) = 1/3
P(Tokyo|C) = 1/3
P(Japan|C) = 1/3
在这个例子中,m为6,即训练集中总共有6个不同的词。把这6个词作为词表,如果测试集中有词不在词表中,不计算。(如果有词出现在测试集,但是不在词表中,我们忽略这个词)
# 这个文章是需要计算是不是China类:
首先计算是China类的概率:
P(Chinese|C) = 5/8 --> 6/14
P(Tokyo|C) = 0/8 --> 1/14
P(Japan|C) = 0/8 --> 1/14
接着计算不是China类的概率:
P(Chinese|C) = 1/3 -->(经过拉普拉斯平滑系数处理) 2/9
P(Tokyo|C) = 1/3 --> 2/9
P(Japan|C) = 1/3 --> 2/9
1.2 案例:商品评论情感分析
学习目标
- 应用朴素贝叶斯API实现商品评论情感分析
1.api介绍
-
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
2.商品评论情感分析
2.1 步骤分析
- 1)获取数据
- 2)数据基本处理
- 2.1) 取出内容列,对数据进行分析
- 2.2) 判定评判标准
- 2.3) 选择停用词
- 2.4) 把内容处理,转化成标准格式
- 2.5) 统计词的个数
- 2.6)准备训练集和测试集
- 3)模型训练
- 4)模型评估
2.2 代码实现
import pandas as pd
import numpy as np
import jieba
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
- 1)获取数据
# 加载数据
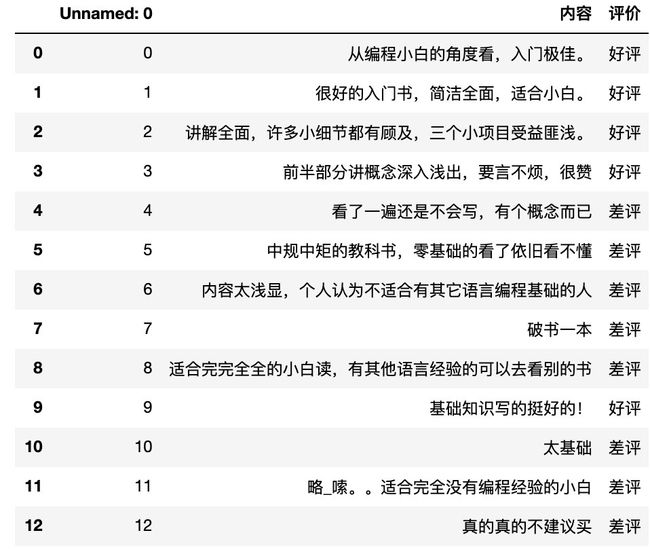
data = pd.read_csv("./data/书籍评价.csv", encoding="gbk",index_col=0)
data
- 2)数据基本处理
# 2.1) 取出内容列,对数据进行分析
content = data["内容"]
content.head()
# 2.2) 判定评判标准 -- 1好评;0差评
data.loc[data.loc[:, '评价'] == "好评", "评论标号"] = 1 # 把好评修改为1
data.loc[data.loc[:, '评价'] == '差评', '评论标号'] = 0
# data.head()
# 2.3) 选择停用词
# 加载停用词
stopwords=[]
with open('./data/stopwords.txt','r',encoding='utf-8') as f:
lines=f.readlines()
print(lines)
for tmp in lines:
line=tmp.strip()
print(line)
stopwords.append(line)
# stopwords # 查看新产生列表
#对停用词表进行去重
stopwords=list(set(stopwords))#去重 列表形式
print(stopwords)
# 2.4) 把“内容”处理,转化成标准格式
comment_list = []
for tmp in content:
print(tmp)
# 对文本数据进行切割
# cut_all 参数默认为 False,所有使用 cut 方法时默认为精确模式
seg_list = jieba.lcut(tmp)
print(seg_list)
seg_str = ' '.join(i for i in seg_list if i !=' ') # 拼接字符串
print(seg_str)
comment_list.append(seg_str) # 目的是转化成列表形式
# print(comment_list) # 查看comment_list列表。
# 2.5) 统计词的个数
# 进行统计词个数
# 实例化对象
# CountVectorizer 类会将文本中的词语转换为词频矩阵
con = CountVectorizer(stop_words=stopwords)#只统计两个词及以上的频率
# 进行词数统计
X = con.fit_transform(comment_list) # 它通过 fit_transform 函数计算各个词语出现的次数
name = con.get_feature_names() # 通过 get_feature_names()可获取词袋中所有文本的关键字
print(X.toarray()) # 通过 toarray()可看到词频矩阵的结果
print(name)
# 2.6)准备训练集和测试集
# 准备训练集 这里将文本前10行当做训练集 后3行当做测试集
labels = data['评论标号'].values
x_train = X.toarray()[:10, :]
y_train = labels[:10]
# 准备测试集
x_text = X.toarray()[10:, :]
y_text = labels[10:]
- 3)模型训练
# 构建贝叶斯算法分类器
mb = MultinomialNB(alpha = 1.0) # alpha 为可选项,默认 1.0,添加拉普拉修/Lidstone 平滑参数
# 训练数据
mb.fit(x_train, y_train)
# 预测数据
y_predict = mb.predict(x_text)
#预测值与真实值展示
print('预测值:',y_predict)
print('真实值:',y_text)
- 4)模型评估
mb.score(x_text, y_text)
测试集
labels = data[‘评论标号’].values
x_train = X.toarray()[:10, :]
y_train = labels[:10]
准备测试集
x_text = X.toarray()[10:, :]
y_text = labels[10:]
- 3)模型训练
```python
# 构建贝叶斯算法分类器
mb = MultinomialNB(alpha = 1.0) # alpha 为可选项,默认 1.0,添加拉普拉修/Lidstone 平滑参数
# 训练数据
mb.fit(x_train, y_train)
# 预测数据
y_predict = mb.predict(x_text)
#预测值与真实值展示
print('预测值:',y_predict)
print('真实值:',y_text)
- 4)模型评估
mb.score(x_text, y_text)