数据结构复习二:线性表
写在前面:考完离散就剩两天复习数据结构,还有七章,我可能要没了……冲冲冲!
什么是线性表
定义是:由n(>=0)个数据特性相同的元素构成的有限序列 n=0时为空表
非空线性结构的特点:
1、“第一个”元素唯一
2、“最后一个”元素唯一
3、除第一个之外,数据结构中的每个数据元素均只有一个前驱
4、除最后一个之外,每个数据元素均只有一个后继
顺序表
定义不再详述,顾名思义。存储结构有随机存取的特点。
用动态分配的一维数组表示顺序表(一般表示),代码如下:
typedef struct{
ElemType *elem; //存储空间基地址
int length; //当前长度
}sqList;用动态分配的一维数组表示顺序表(以一元多项式的顺序存储结构为例),代码如下:
typedef struct{
float coef; //系数
int expn; //指数
}Polynomial;
typedef struct{
Polynomial *elem; //存储空间的基地址
int length; //多项式中当前项的个数
}sqList;顺序表中基本操作的实现
1、初始化
算法步骤:为表L动态分配一个预定义大小的数组空间,使elem指向这段空间的地址,并将当前表长设为0。
代码实现:
L.elem=new ElemType[maxn]; //为顺序表分配一个大小为maxn的空间
if(!L.elem) exit(OVERFLOW); //存储分配失败退出特别注意程序运行失败的出口!
2、取值
算法步骤:判断指定位置序号i值是否合理,若i值合理,则将对应数据元素L.elem[i-1]赋给参数e,通过e返回第i个数据元素的值,否则返回ERROR。
注意算法步骤的逻辑!先判断后执行
代码不再给出。
时间复杂度显然是O(1)。
3、查找
查找的算法会在以后的内容专门作为一部分详细说明,这里的查找只有顺序遍历,时间复杂度为O(n)。
4、插入
算法步骤:
1、判断位置i是否合法
2、判断顺序表存储空间是否合法
3、将n至第i个元素依次向后移动一个位置,空出第i个位置
4、将要插入的新元素e放入第i个位置
5、length++
同样注意算法的逻辑!
代码不再给出,下面进行时间复杂度分析:
在第i个元素之前插入的概率是 ![]() ,移动次数为
,移动次数为![]() ;
;
那么在长度为n的线性表中插入一个元素时所需移动元素次数的期望值是: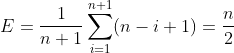
由此可见平均时间复杂度为O(n)。
5、删除
算法步骤:
1、判断删除位置i是否合法
2、将第i+1个至第n个位置的元素依次向前移动一个位置
3、length--
链表
即线性表的链式存储结构,特点是用一组任意的存储单元存储线性表的数据元素(连续或不连续)
存储内容包括本身的信息以及直接后继的存储位置,分别称为数据域和指针域
根据链表结点所含指针个数、指针指向和指针连接方式,可将链表分为单链表、循环链表、双向链表、二叉链表、十字链表、邻接表、邻接多重表等。
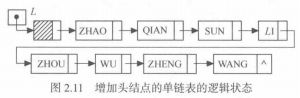
单链表的定义及表示
头结点可加可不加,增加后操作较为便利。
单链表可由头指针唯一确定,非随机存取,存储结构代码如下:
typedef struct LNode{
ElemType data; //结点的数据域
struct LNode *next; //结点的指针域
}LNode,*LinkList; //LinkList为LNode的指针类型,定义时LNode *p与LinkList p完全相同单链表基本操作的实现
1、初始化
L=new LNode; //生成新结点作为i头节点,用头指针L指向头结点
L->next=NULL; //头结点指针域置空2、取值
p=p->next遍历操作,比较简单,不再详述。
时间复杂度为O(n)。
3、查找
也是遍历,时间复杂度同上
4、插入
也比较简单,主要是找到位置,创建新结点并插入,关键代码:
s->next=p->next; //两个p->next可分别理解为一个有值的结点
p->next=s; //一片待赋值的空间5、删除
主要代码:
q=p->next;
p->next=q->next; //将待删除结点的前驱结点的后继指向待删除结点的后继
delete q;
6、创建单链表
这里是个小小的重点
前插法创建单链表
算法步骤:
1、创建一个只有头结点的空链表
2、根据带创建链表包括的元素个数n,循环n次执行以下操作:
(1)生成一个新结点*p
(2)输入元素值赋给新结点*p的数据域
(3)将新结点*p插入到头结点之后
代码实现:
void CreateList_H(LinkList &L, int n)
{
LinkList p;
L = new LNode;
L->next = NULL;
for (int i = 0; i < n; i++)
{
p = new LNode;
cin >> p->data;
p->next = L->next;
L->next = p;
}
}时间复杂度显然为O(n)。
这里每次从头插入元素,所得链表顺序为原数组逆序,所以实际写代码时一般用后插法
后插法创建单链表
算法步骤:
1、创建一个只有头结点的空链表
2、尾指针r初始化,指向头结点
3、根据创建链表包括的元素个数n,循环n次执行以下操作
(1)生成一个新结点*p
(2)输入元素值赋给新结点*p的数据域
(3)将新结点*p插入到尾结点*r之后
(4)尾指针指向新的尾结点*p
代码实现:
void CreateList_R(LinkList &L, int n)
{
LinkList r, p;
L = new LNode;
L->next = NULL;
r = L;
for (int i = 0; i < n; i++)
{
p = new LNode;
cin >> p->data;
p->next = NULL;
r->next = p;
r = p;
}
}这里如果把r看成一个外部的东西会很难理解,就直接看成当前指针吧,比如刚开始时就把r看作跟L一样的东西(实际上代码里也是这么表现的),后面的r就是每一步的p。
时间复杂度也是n。
循环链表
特点是表中最后一个结点的指针域指向头结点,整个链表形成一个环。
判断当前指针是否指向表为结点的终止条件由p!=NULL或p->next!=NULL变为p!=L或p->next!=L。
有时循环链表中只设立尾指针,这样会简化链表的合并操作。
双向链表
结点中由两个指针域,一个指向直接后继,另一个指向直接前驱
存储结构:
typedef struct DuLNode{
ElemType data;
struct DuLNode *prior;
struct DuLNode *next;
}DuLNode,*DuLinkList;双向链表的插入、删除操作涉及两个方向上的指针,与单链表有很大不同,其他操作与单链表没有什么不同
双向链表的插入,主要代码:
s->prior=p->prior;
p->prior->next=s;
s->next=p;
p->prior=s;删除要简单一些:
p->prior->next=p->next;
p->next->prior=p->prior;两者时间复杂度均为O(n)。
顺序表和链表的比较
1、空间性能的比较
基于存储空间的分配以及存储密度的大小,当线性表的长度变化比较大,难以预估存储规模时,宜采用链表作为存储结构
反之,当线性表长度变化不大,易于事先确定大小时,为了节约存储空间,宜采用顺序表作为存储结构
附:存储密度=数据元素本身占用的存储量 / 结点结构占用的存储量
2、时间性能的比较
基于存取元素的效率以及插入和删除操作的效率,若先行表的主要操作是和元素位置紧密相关的这类取值操作,很少做插入或删除操作时,宜采用顺序表作为存储结构
反之,对于频繁进行插入或删除操作的先行表,宜采用链表作为存储结构
————————————————————————————————————————————————————
注:本文所有内容均来源于《数据结构(C语言第二版)》(严蔚敏老师著)
目录
什么是线性表
顺序表
顺序表中基本操作的实现
1、初始化
2、取值
3、查找
4、插入
5、删除
链表
单链表的定义及表示
单链表基本操作的实现
1、初始化
2、取值
3、查找
4、插入
5、删除
6、创建单链表
循环链表
双向链表
顺序表和链表的比较
1、空间性能的比较
2、时间性能的比较