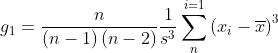数据分析方法——第1章

一、背景

教材：数据分析方法 第二版 梅长林 范金城 编

软件：SAS 9.4（中文（简体））

【软件】：SAS 8.2

二、内容目录

第1章 数据描述性分析

        1.1 一维数据的数字特征

                1.1.1 表示位置的数字特征

                1.1.2 表示分散性的数字特征

                1.1.3 表示分布形状的数字特征

三、正文内容

1.1.1 表示位置的数字特征

n个一维数据，，...，——从总体X中观测得到的n个样本观测值，n为样本容量。

1.均值mean

数据中存在异常值时，均值缺乏抗扰性或稳健性，即易受异常值的影响而使其值有较大的变化。

2.中位数Median

受异常值的影响较小，具有较好的抗扰性或稳健性。

3.分位数

上、下四分位数：0.75分位数、0.25分位数

，

4.三均值

SAS 程序通常分为数据步和过程步，一段SAS 程序根据目的和需要可以有0到多个数据步（Data）和0到多个过程步（Proc），还可以有系统选项语句、ODS语句等全局语句。

1.数据步（Data Step）

         以关键词Data 开头，可由多条语句构成，结束标志可以是空语句、Run 语句、过程步或下一步数据步。

         数据步功能有:
        （1）从外部文件中读取数据；
        （2）将数据写入到外部文件中；
        （3）读取SAS数据文件和视图；
        （4）创建SAS数据文件和视图。

 2.过程步（Proc Step）

        以关键词Proc 开头，可由多条语句构成，结束标志是Run或Quit 语句。

        过程步的功能有：
        （1）调用 SAS 过程(SAS Procedures)分析和处理SAS数据集形式的数据，或执行其他分析；
        （2）将分析结果以报表、图表的形式输出，或输出成 SAS数据集、外部文件；
        （3）生成SQL查询；
        （4）数据操作和管理。

proc univariate：对单变量做统计分析

例1.1 对某学校100名女学生测定血清蛋白含量（单位：g/L），数据如下：

74.3 78.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.5
79.5 75.6 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0
75.0 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.0
73.5 75.0 72.0 64.3 75.8 80.3 69.7 74.3 73.5 73.5
75.8 75.8 68.8 76.5 70.4 71.2 81.2 75.0 70.4 68.0
70.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.3
73.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.7
67.2 76.5 72.7 70.4 77.2 68.8 67.3 67.3 67.3 72.7
75.8 73.5 75.0 72.7 73.5 73.5 72.7 81.6 70.3 74.3
73.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.5 70.4

计算均值，中位数，上、下四分位数，，，，，，分位数及三均值

data examp1_1;
input x @@;
/*input描述数据行或外部输入文件上的记录*/
/*@@是读取数据值的指针控制符号，指定在同一个数据行可以读取2个以上的观测数据*/
/*cards标识数据行的开始*/
cards;
74.3 78.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.5
79.5 75.6 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0
75.0 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.0
73.5 75.0 72.0 64.3 75.8 80.3 69.7 74.3 73.5 73.5
75.8 75.8 68.8 76.5 70.4 71.2 81.2 75.0 70.4 68.0
70.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.3
73.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.7
67.2 76.5 72.7 70.4 77.2 68.8 67.3 67.3 67.3 72.7
75.8 73.5 75.0 72.7 73.5 73.5 72.7 81.6 70.3 74.3
73.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.5 70.4
;
proc univariate data=examp1_1; 
/*PROC指示过程步的开始，后接过程名，univariate为SAS过程名，’data’为数据集选项*/
/*univariate对单变量做统计分析，可以生成一系列统计量和图表*/
var x;
 /*var后跟变量名，指定分析的变量*/
run;

矩
N	100	权重总和	100
均值	73.66	观测总和	7366
标准差	3.94008153	方差	15.5242424
偏度	0.06007521	峰度	0.03386864
未校平方和	544116.46	校正平方和	1536.9
变异系数	5.34901103	标准误差均值	0.39400815

Moments：矩统计量
N：观测数据个数
Sum Weights：权重总和
Mean：均值，加权平均或算数平均，当没有指定权重时，就是算数平均（即每个观测的权重为1）
Sum Observations：观测值总和。等于 N*Mean
Std Deviation：标准差。等于方差求根号运算。SD衡量一组数据的离散程度。
Variance：方差。这里 d 是自由度，默认等于 n-1。
Skewness：偏度。用来衡量变量分布的偏斜度。偏度的取值范围为(-∞,+∞) . 当偏度<0时，概率分布图左偏。当偏度=0时，表示数据相对均匀的分布在平均值两侧，不一定是绝对的对称分布。当偏度>0时，概率分布图右偏。
Kurtosis：峰度。用来衡量变量分布的顶部陡峭程度。峰度的取值范围为[1,+∞), 正态分布的峰度值为 3, 超过3说明变量分布是尖峰的, 低于3说明峰度更平缓。
Uncorrected SS：未校平方和
Corrected SS：校正平方和
Coeff Variation：变异系数。是样本标准差(sample standard deviation) 和样本均值的比值。用来衡量样本的离散程度, CV 越大表示数据分布越离散。单位：%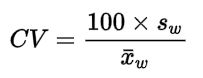

Std Error Mean：标准误差均值 (Standard Error of Mean, SE)。
SE是样本统计量的标准差，是衡量样本抽样的误差的指标, SE越小说明抽样误差越小。

基本统计测度
位置		变异性
均值	73.66000	标准差	3.94008
中位数	73.50000	方差	15.52424
众数	73.50000	极差	20.00000
		四分位间距	4.60000

Basic Statistical Measures：基本统计测度
Location：位置
Variability：变异性
Mean：均值
Std Deviation：标准差
Median：中位数
Variance：方差
Mode：众数
Range：极差
Interquartile Range：四分位间距

位置检验: Mu0=0
检验	统计量		p 值
Student t	t	186.9504	Pr > |t|	<.0001
符号检验	M	50	Pr >= |M|	<.0001
符号秩检验	S	2525	Pr >= |S|	<.0001

Test for Location：位置检验
Test Statistic：检验
Value：统计量
p-value：p值
Student's t：t检验
Sign M：符号检验
Signed Rank S：符号秩检验

分位数（定义 5）
水平	分位数
100% 最大值	84.30
99%	82.95
95%	80.50
90%	79.15
75% Q3	75.80
50% 中位数	73.50
25% Q1	71.20
10%	68.40
5%	67.30
1%	64.65
0% 最小值	64.30

Quantiles（Definition 5）：分位数（定义5）
Quantile：水平
Estimate：分位数
Max：最大值
Med：中位数
Min：最小值

极值观测
最小值		最大值
值	观测	值	观测
64.3	34	80.5	7
65.0	65	81.2	47
65.0	26	81.6	67
67.2	71	81.6	88
67.3	79	84.3	97

Extreme Observations：极值观测
Value：值
Obs：Observation，观测值

1.1.2 表示分散性的数字特征

1.方差、标准差及变异系数

Variance：方差
Std Deviation：标准差
 Coeff Variation：变异系数。是样本标准差(sample standard deviation) 和样本均值的比值。用来衡量样本的离散程度, CV 越大表示数据分布越离散。单位：%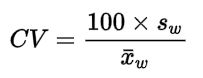

2.极差与四分位极差

Range：极差
四分位极差：

总体方差
总体标准差
总体变异系数
样本容量n充分大时，，，

正态分布（，）四分位标准差

在数据分析中，判断异常值的简便方法：，分别为数据的下、上截断点，大于上截断点的数据、小于下截断点的数据均被视为异常值

例1.2（续例1.1）求例1.1血清蛋白含量数据的方差、标准差、变异系数、极差、四分位极差、四分位标准差，并分析是否有异常值。

data examp1_1;
input x @@;
cards;
74.3 78.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.5
79.5 75.6 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0
75.0 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.0
73.5 75.0 72.0 64.3 75.8 80.3 69.7 74.3 73.5 73.5
75.8 75.8 68.8 76.5 70.4 71.2 81.2 75.0 70.4 68.0
70.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.3
73.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.7
67.2 76.5 72.7 70.4 77.2 68.8 67.3 67.3 67.3 72.7
75.8 73.5 75.0 72.7 73.5 73.5 72.7 81.6 70.3 74.3
73.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.5 70.4
;
proc univariate data=examp1_1;
var x;
run;

data delmax;
set examp1_1;
if x=84.3 then delete;
run;

proc univariate data=delmax;
var x;
run;

异常值为84.3，建立删除该值的数据集delmax

SAS 系统

UNIVARIATE PROCEDURE

变量: x

矩
N	99	权重总和	99
均值	73.5525253	观测总和	7281.7
标准差	3.80995858	方差	14.5157844
偏度	-0.0733008	峰度	-0.1523519
未校平方和	537009.97	校正平方和	1422.54687
变异系数	5.1799154	标准误差均值	0.38291524

基本统计测度
位置		变异性
均值	73.55253	标准差	3.80996
中位数	73.50000	方差	14.51578
众数	73.50000	极差	17.30000
		四分位间距	4.60000

位置检验: Mu0=0
检验	统计量		p 值
Student t	t	192.0857	Pr > |t|	<.0001
符号检验	M	49.5	Pr >= |M|	<.0001
符号秩检验	S	2475	Pr >= |S|	<.0001

分位数（定义 5）
水平	分位数
100% 最大值	81.6
99%	81.6
95%	80.5
90%	78.8
75% Q3	75.8
50% 中位数	73.5
25% Q1	71.2
10%	68.0
5%	67.3
1%	64.3
0% 最小值	64.3

极值观测
最小值		最大值
值	观测	值	观测
64.3	34	80.5	6
65.0	65	80.5	7
65.0	26	81.2	47
67.2	71	81.6	67
67.3	79	81.6	88

1.1.3 表示分布形状的数字特征

1.偏度

Skewness：偏度

2.峰度

Kurtosis：峰度

例1.3 从1952年至2001年我国国民生产总值、第一产业（农业）、第二产业（工业与建筑业）、第三产业的产值见表1.1（单位：亿元）.分别计算国民生产总值，第一、二、三产业产值的主要数字特征并考察异常值情况

data examp1_3;
input year x x1 x2 x3;
cards;
1952      679.0      342.9      141.8      194.3
1953      824.0      378.0      192.5      253.5
1954      859.0      392.0      211.7      255.3
1955      910.0      421.0      222.2      266.8
1956     1028.0      443.9      280.7      303.4
1957     1068.0      430.0      317.0      321.0
1958     1307.0      445.9      483.5      377.6
1959     1439.0      383.8      615.5      439.7
1960     1457.0      340.7      648.2      468.1
1961     1220.0      441.1      388.9      390.0
1962     1149.3      453.1      359.3      336.9
1963     1233.3      497.5      407.6      328.2
1964     1454.0      559.0      513.5      381.5
1965     1716.1      651.1      602.2      462.8
1966     1868.0      702.2      709.5      456.3
1967     1773.9      714.2      602.8      456.9
1968     1723.1      726.3      537.3      459.5
1969     1937.9      736.2      689.1      512.6
1970     2252.7      793.3      912.2      547.2
1971     2426.4      826.3     1022.8      577.3
1972     2518.1      827.4     1084.2      606.5
1973     2720.9      907.5     1173.0      640.4
1974     2789.9      945.2     1192.0      652.7
1975     2997.3      971.1     1370.5      655.7
1976     2943.7      967.0     1337.2      639.5
1977     3201.9      942.1     1509.1      750.7
1978     3624.1     1018.4     1745.2      860.5
1979     4038.2     1258.9     1913.5      865.8
1980     4517.8     1359.4     2192.0      966.4
1981     4862.4     1545.6     2255.5     1061.3
1982     5294.7     1761.6     2383.0     1150.1
1983     5934.5     1960.8     2646.2     1327.5
1984     7171.0     2295.5     3105.7     1769.8
1985     8664.4     2541.6     3866.6     2256.2
1986    10202.2     2763.9     4492.7     2945.6
1987    11962.5     3204.3     5251.6     3506.6
1988    14928.3     3831.0     6587.2     4510.1
1989    16909.2     4228.0     7278.0     5403.2
1990    18547.9     5017.0     7717.4     5813.5
1991    21617.8     5288.6     9102.2     7227.0
1992    26638.1     5800.0    11699.5     9138.6
1993    34634.4     6882.1    16428.5    11323.8
1994    46759.4     9457.2    22372.2    14930.0
1995    58478.1    11993.0    28537.9    17947.2
1996    67884.6    13844.2    33612.9    20427.5
1997    74462.6    14211.2    37222.7    23028.7
1998    78345.2    14552.4    38619.3    25173.5
1999    81910.9    14457.2    40417.9    27035.8
2000    89403.6    14212.0    45487.8    29703.8
2001    95933.3    14609.9    49069.1    32254.3
;
run;

proc univariate data=examp1_3;
var x x1 x2 x3;
run;

时间：2022年11月8日