多元分析——聚类分析【数学建模】

多元分析是多变量的统计分析方法。

聚类分析（群分析），是对多个样本或指标进行定量分类的一种多元化统计分析方法。对样本进行分类成为Q型聚类分析，对指标进行分类称为R型聚类分析。

分类是已知类别的，聚类是未知。

Q型聚类分析

样本的相似性度量

要用数量化的方法对事物进行分类，就必须用数量化的方法描述事物之间的相似程度。一个事物常常需要用多个变量来刻画。如果对于一群有待分类的样本点需用 p 个变量描述，则每个样本点可以看成是 Rp 空间中的一个点。因此，很自然地想到可以用距离来度量样本点间的相似程度。



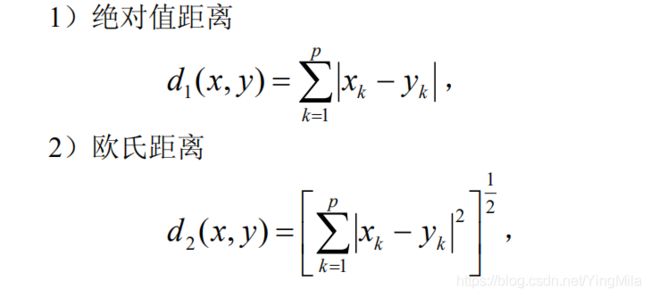
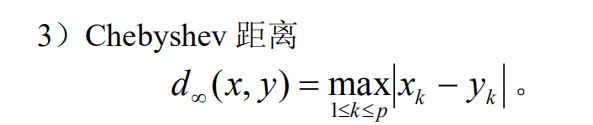
欧氏距离最常用，主要优点是当坐标轴进行正交旋转时，欧氏距离是保持不变的。 因此，如果对原坐标系进行平移和旋转变换，则变换后样本点间的距离和变换前完全相同。

值得注意的是在采用 Minkowski 距离时，一定要采用相同量纲的变量。如果变量的量纲不同，测量值变异范围相差悬殊时，建议首先进行数据的标准化处理，然后再计算距离。
在采用 Minkowski 距离时，还应尽可能地避免变量的多重相关性。多重相关性所造成的信息重叠，会片面强调某些变量的重要性。

由于 Minkowski 距离的这些缺点，一种改进的距离就是马氏距离，定义如下

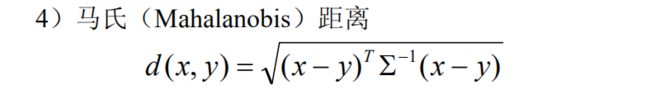
其中 x, y 为来自 p 维总体 Z 的样本观测值，Σ 为 Z 的协方差矩阵，实际中Σ 往往是不知道的，常常需要用样本协方差来估计。

马氏距离对一切线性变换是不变的，故不受量纲的影响。

类与类间的相似性度量

如果有两个样本类G1和G2 ，我们可以用下面的一系列方法度量它们间的距离：



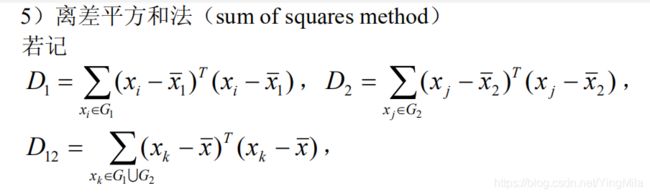
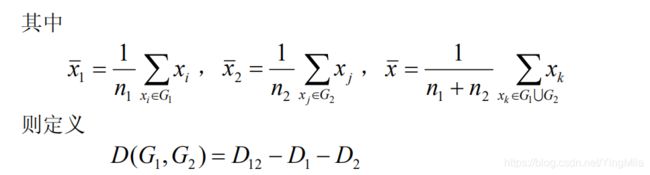
事实上，若 G1 ,G2 内部点与点距离很小，则它们能很好地各自聚为一类，并且这两类又能够充分分离（即 D12 很大），这时必然有 D = D12 − D1 − D2很大。因此，按定义可以认为，两类 G1 ,G2 之间的距离很大。离差平方和法又称为 Ward 方法。

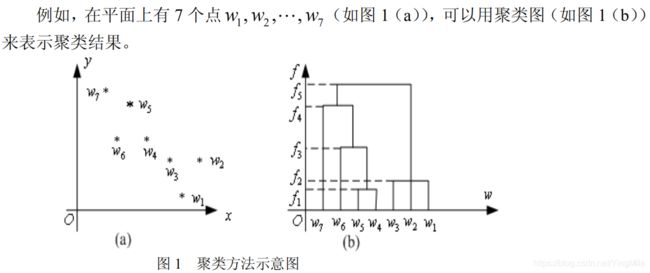
聚类图

系统聚类法是聚类分析方法中最常用的一种方法。它的优点在于可以指出由粗到细的多种分类情况，典型的系统聚类结果可由一个聚类图展示出来。

最短距离法的聚类举例

如果使用最短距离法来测量类与类之间的距离，即称其为系统聚类法中的最短距离法（又称最近邻法）。
例：


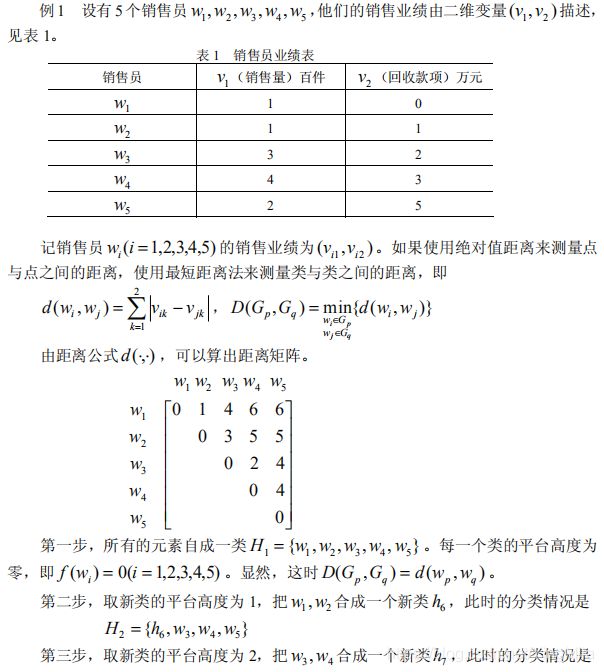
计算的Matlab程序：

clc,clear 
a=[1,0;1,1;3,2;4,3;2,5]; 
[m,n]=size(a); 
d=zeros(m); 
for i=1:m 
 for j=i+1:m 
 d(i,j)=mandist(a(i,:),a(j,:)'); 
 %求第一个矩阵的行向量与第二个矩阵的列向量之间对应的绝对值距离
 end 
end 
d 
nd=nonzeros(d); %去掉d中的零元素，非零元素按列排列
nd=union(nd,nd) %去掉重复的非零元素
for i=1:m-1 
 nd_min=min(nd); 
 [row,col]=find(d==nd_min);tm=union(row,col); %row和col归为一类
 tm=reshape(tm,1,length(tm)); %把数组tm变成行向量 
 fprintf('第%d次合成，平台高度为%d时的分类结果为：%s\n',... 
 i,nd_min,int2str(tm)); 
 nd(find(nd==nd_min))=[]; %删除已经归类的元素
 if length(nd)==0 
 break 
 end 
end 

或者使用MATLAB统计工具箱的相关命令，编写如下程序：

clc,clear 
a=[1,0;1,1;3,2;4,3;2,5]; 
y=pdist(a,'cityblock'); %求a的两两行向量间的绝对值距离
yc=squareform(y) %变换成距离方阵
z=linkage(y) %产生等级聚类树
[h,t]=dendrogram(z) %画聚类图
T=cluster(z,'maxclust',3) %把对象划分成3类
for i=1:3 
 tm=find(T==i); %求第i类的对象
 tm=reshape(tm,1,length(tm)); %变成行向量
 fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end

Matlab 聚类分析的相关命令

pdist

Y=pdist(X)计算 m× n 矩阵X（看作m 个 n 维行向量）中两两对象间的欧氏距离。
对于有m 个对象组成的数据集，共有(m −1)⋅ m / 2个两两对象组合。

linkage

Z=linkage(Y)使用最短距离算法生成具层次结构的聚类树。输入矩阵Y为pdist函数输出的(m −1)⋅ m / 2维距离行向量。

cluster

T=cluster(Z,cutoff)从连接输出（linkage）中创建聚类。cutoff为定义cluster函数如何生成聚类的阈值

zsore(X)

H=dendrogram(Z,P)

由linkage产生的数据矩阵Z画聚类树状图。P是结点数，默认值是30。

T=clusterdata(X,cutoff)

squareform

将pdist的输出转换为方阵。

R型聚类

在系统分析或评估过程中，为避免遗漏某些重要因素，往往在一开始选取指标时，尽可能多地考虑所有的相关因素。
而这样做的结果，则是变量过多，变量间的相关度高，给系统分析与建模带来很大的不便。

因此，人们常常希望能研究变量间的相似关系，按照变量的相似关系把它们聚合成若干类，进而找出影响系统的主要因素。

变量的相似性度量

在对变量进行聚类分析时，首先要确定变量的相似性度量，常用的变量相似性度量有两种。

相关系数

夹角余弦

变量聚类法

类似于样本集合聚类分析中最常用的最短距离法、最长距离法等，变量聚类法采用了与系统聚类法相同的思路和过程。

最长距离法

最短距离法