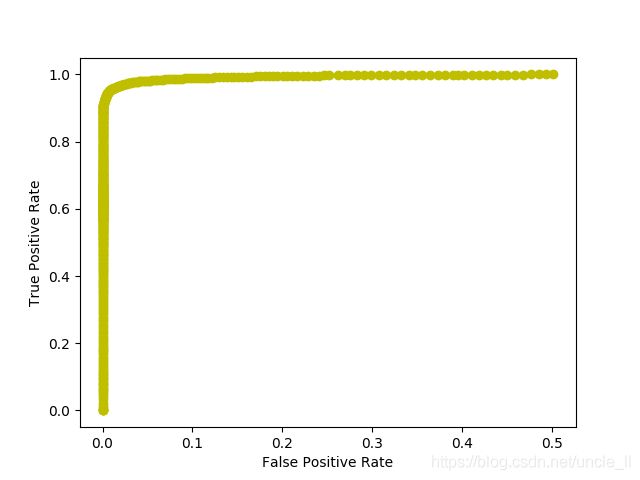
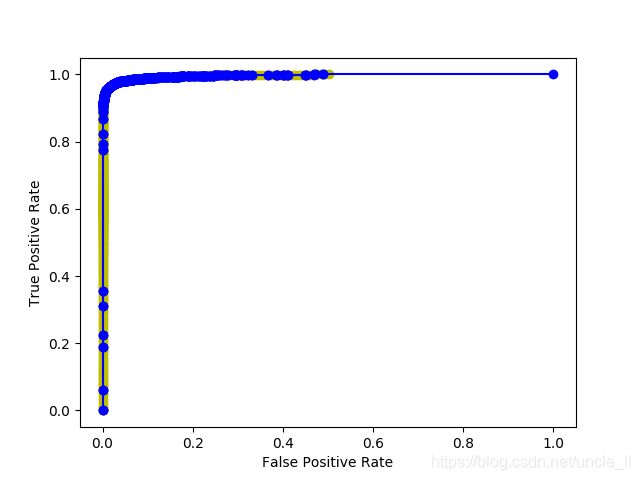
二分类确定画出roc曲线，以及基于roc曲线获得最佳划分阈值

问题

在做二分类问题时候，有正样本和负样本。构建的算法，针对每个样本会输出一个分数值。假设该分数大小为[0, 1]区间内的值。有时候单纯地以分数0.5位阈值划分样本为预测为1或者预测为0，效果有时候并不好，此时如何确定很好的阈值分数呢？答案是可以利用roc曲线来确定比较好的划分阈值。

ROC曲线介绍

二分类过程，设定阈值，大于该分数为1，小于该分数为0，统计计算TP， FN， FP，TN等数据计算FPR，TPR

---

• p(positive): 标签1
• n(negative): 标签0
• t(true): 预测正确
• f(false): 预测错误

---

• TP: 实例是正类并被预测成正类 正确预测正类（把正类预测正类）
• FP：实例是负类并被预测成正类 错误预测正类（把负类预测为正类）
• TN：实例是负类并被预测成负类 正确预测负类（把负类预测为负类）
• FN：实例是正类并被预测为负类 错误预测负类 （把正类预测为负类）

---

        |          -      |     实际表现           |
        ---------------------------------------------------
        |                |      1        0       |   合计
        |--------------------------------------------------
        |           | 1  |     11(TP)    01(FP)  |   TP+FP
        | 预测表现   |    |                       |
        |           |  0 |     10(FN)    00(TN)  |   FN+TN
        | ----------------------------------------------------------
        |   合计        |       TP+FN      FP+TN |  TP + FP + FN + TN
        -------------------------------------------------------------

• 真正类率(TPR)：TPR = TP/(TP+FN) 刻画的是分类器所识别出的 正实例占所有正实例的比例 灵敏度

• 负正类率(FPR): FPR = FP/(FP+TN) 计算的是分类器错认为正类的负实例占所有负实例的比例 1-特异度

• 真负类率(TNR): TNR = TN/(FP+TN) = 1-FPR 分类器所识别出的负实例占所有负实例的比例 特异度

• 准确率： accuracy = (TP+TN) / (TP+TN+FP+FN) 准确率的定义是预测正确的结果占总样本的百分比, 样本不均衡时候不好

• 精准率： precision = TP / (TP+FP) 所有被预测为正的样本中实际为正的样本的概率

• 召回率（查全率）： recall = TP / (TP+FN) 在实际为正的样本中被预测为正样本的概率

• P-R曲线：查准率-查全率， 希望查准率和查全率同时高，但不现实

• F1分数均衡：F1_score = (2pr)/(p+r)

• ROC曲线： 横坐标FPR， 纵坐标TPR

代码实现

两种方式：

• 自己遍历统计计算
• 调用skearln中的相关计算包

#!/bin/python
# fileUsing: 画出ROC曲线，并熟悉混淆矩阵相关的知识

import sys
import numpy as np
from sklearn import metrics
from sklearn.metrics import auc
import matplotlib.pyplot as plt


class DrawRoc(object):
    def __init__(self):
        pass

    def draw_roc(self, predict_scores: list, ture_labelsi: list) -> float:
        """二分类过程，设定阈值，大于该分数为1，小于该分数为0，统计计算TP， FN， FP，TN等数据
            计算FPR，TPR
            p(positive): 标签1
            n(negative): 标签0
            t(true): 预测正确
            f(false): 预测错误
            TP: 实例是正类并被预测成正类  正确预测正类（把正类预测正类）
            FP：实例是负类并被预测成正类  错误预测正类（把负类预测为正类）
            TN：实例是负类并被预测成负类  正确预测负类（把负类预测为负类）
            FN：实例是正类并被预测为负类  错误预测负类 （把正类预测为负类）
            -----------------------------------------
            |                |     实际表现           |
            ---------------------------------------------------
            |                |      1        0       |   合计
            |--------------------------------------------------
            |           | 1  |     11(TP)    01(FP)  |   TP+FP
            | 预测表现   |    |                       |
            |           |  0 |     10(FN)    00(TN)  |   FN+TN
            | ----------------------------------------------------------
            |   合计        |       TP+FN      FP+TN |  TP + FP + FN + TN
            -------------------------------------------------------------
            真正类率(TPR)：TPR = TP/(TP+FN)  刻画的是分类器所识别出的 正实例占所有正实例的比例  灵敏度
            负正类率(FPR): FPR = FP/(FP+TN)  计算的是分类器错认为正类的负实例占所有负实例的比例 1-特异度
            真负类率(TNR): TNR = TN/(FP+TN) = 1-FPR 分类器所识别出的负实例占所有负实例的比例 特异度

            准确率： accuracy = (TP+TN) / (TP+TN+FP+FN)  准确率的定义是预测正确的结果占总样本的百分比, 样本不均衡时候不好
            精准率： precision = TP / (TP+FP)  所有被预测为正的样本中实际为正的样本的概率
            召回率（查全率）： recall = TP / (TP+FN)  在实际为正的样本中被预测为正样本的概率
            P-R曲线：查准率-查全率， 希望查准率和查全率同时高，但不现实
            F1分数均衡：F1_score = (2*p*r)/(p+r)
            ROC曲线： 横坐标FPR， 纵坐标TPR
        """
        ths = list(np.linspace(0, 1, 100))  # 阈值 分100等分
        tprs = []
        fprs = []
        diffs = []
        auc = 0
        # 开始计算
        for th in ths:
            tp = 0
            tn = 0
            fp = 0
            fn = 0
            predict_labels = [1 if score >= th else 0 for score in predict_scores]  # 大于等于阈值时候，判定为预测为正
            length = len(predict_labels)
            for idx in range(len(predict_labels)):
                predict_label = predict_labels[idx]
                ture_label = ture_labels[idx]
                if ture_label == 1 and predict_label == 1:
                    tp += 1
                if ture_label == 1 and predict_label == 0:
                    fn += 1
                if ture_label == 0 and predict_label == 0:
                    tn += 1
                if ture_label == 0 and predict_label == 1:
                    fp += 1
            tpr = tp / (tp+fn)
            fpr = fp / (fp+tn)
            tprs.append(tpr)
            fprs.append(fpr)
            diffs.append(tpr-fpr)

        # get fpr tpr ths and plot
        plt.plot(fprs, tprs, 'yo-')
        plt.ylabel('True Positive Rate')
        plt.xlabel('False Positive Rate')
        plt.show()
        plt.savefig('roc1.png')

        # calc auc, 受样本影响大，除非全是正样本，无负样本时候，使用类似微积方法计算得到的面积才对
        """
        fprs_tprs = []
        for i in range(len(ths)):
            fpr = tprs[i]
            tpr = fprs[i]
            fprs_tprs.append([fpr, tpr])
        fprs_tprs.sort(key=lambda x:x[0], reverse=False)
        for i in range(1, len(ths)):
            fpr, tpr = fprs_tprs[i-1]
            fpr_i, tpr_i = fprs_tprs[i]
            height = tpr_i
            weight = fpr_i - fpr
            auc += height * weight
        print("auc1:", auc)
        """

        # get best th
        max_diff = max(diffs)
        optimal_idx = diffs.index(max_diff)
        optimal_th = ths[optimal_idx]
        return optimal_th

    def draw_roc_by_sklearn(self, predict_scores: list, ture_labels: list) -> float:
        score = np.array(predict_scores)
        y = np.array(ture_labels)
        fpr, tpr, thresholds = metrics.roc_curve(y, score)
        auc = metrics.auc(fpr, tpr)
        print("auc2:", auc)
        optimal_idx = np.argmax(tpr - fpr)
        optimal_th = thresholds[optimal_idx]
        plt.plot(fpr, tpr, 'bo-')
        plt.ylabel('True Positive Rate')
        plt.xlabel('False Positive Rate')
        plt.show()
        plt.savefig('roc2.png')
        return optimal_th


if __name__ == '__main__':
    dr = DrawRoc()
    right_scores_file = sys.argv[1]  # 正确样本的分数列表
    error_scores_file = sys.argv[2]   # 错误样本的分数列表
    predict_scores = []
    ture_labels = []
    with open(right_scores_file) as f:
        for line in f:
            data = line.rstrip('\n')
            if data:
                score = float(data)
                predict_scores.append(score)
                ture_labels.append(1)

    with open(error_scores_file) as f:
        for line in f:
            data = line.rstrip('\n')
            if data:
                score = float(data)
                predict_scores.append(score)
                ture_labels.append(0)
    th1 = dr.draw_roc(predict_scores, ture_labels)
    print("th1:", th1)
    th2 = dr.draw_roc_by_sklearn(predict_scores, ture_labels)
    print("th2:", th2)

结果

• roc1
  
• roc2
  

参考

• https://blog.csdn.net/ybdesire/article/details/51999995
• https://zhuanlan.zhihu.com/p/25212301
• https://www.cnblogs.com/nxld/p/6365637.html
• https://zhuanlan.zhihu.com/p/32824418
• https://blog.csdn.net/qq_34840129/article/details/85253932
• https://www.cnblogs.com/nxld/p/6365637.html
• https://stackoverflow.com/questions/28719067/roc-curve-and-cut-off-point-python
• https://blog.csdn.net/ZYC88888/article/details/103755818
• https://zhuanlan.zhihu.com/p/46714763（推荐）