【GAMES 101】作业1的实现和思考

本文为闫令琪老师的GAMES 101课程的作业1的个人实现与一些简单的思考，文中如有错漏欢迎指出。

作业要求

本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个点v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形。

代码实现

这里需要实现的是get_model_matrix和get_projection_matrix这两个方法，分别对应着模型和投影变换。

在模型变换中，要实现绕z轴旋转rotation_angle角度的变换矩阵，即为如下所示的矩阵：

$$R_z(\alpha )=\left[\begin{array}{cccc}cos\alpha & -sin\alpha & 0& 0\\ sin\alpha & cos\alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

投影变换参考闫老师课上讲解的方法实现：

正交投影变换是先将长方体平移到中心在原点的位置，再缩放成边长为2的正方体

$$M_{ortho}=M_{scale}\cdot M_{transform}$$

透视投影变换是先将平截头体变形成长方体，再进行正交投影变换

$$M_{persp}=M_{ortho}\cdot M_{persp2ortho}$$

将平截头体变形成长方体，满足的两个规则是：

Rule1：近平面的点不变

Rule2：远平面的点z值不变

根据这两个规则和相似三角形，可以推出平截头体变形成长方体的变换矩阵：

$$M_{persp2ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$$

由此我们得到了最终的投影变换矩阵。

投影变换的详细图示与推导可以阅读这位同学的博文：参考文章

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
	Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

	// TODO: Implement this function
	// Create the model matrix for rotating the triangle around the Z axis.
	// Then return it.

	double radian = MY_PI * rotation_angle / 180;

	Eigen::Matrix4f translate;
	translate << cos(radian), -sin(radian), 0, 0,
				 sin(radian), cos(radian), 0, 0,
				 0, 0, 1, 0,
				 0, 0, 0, 1;
	model = translate * model;

	return model;
}

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
	float zNear, float zFar)
{
	// Students will implement this function

	Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

	// TODO: Implement this function
	// Create the projection matrix for the given parameters.
	// Then return it.
	Eigen::Matrix4f scale;
	Eigen::Matrix4f translate;
	Eigen::Matrix4f persp2ortho;

	double halfFov = MY_PI * 0.5 * eye_fov / 180;
	double top = tan(halfFov) * zNear;
	double bottom = -top;
	double right = aspect_ratio * top;
	double left = -right;
	double near = -zNear;	// zNear和zFar是正的，但z值应该是负的
	double far = -zFar;

	scale << 2 / (right - left), 0, 0, 0,
		0, 2 / (top - bottom), 0, 0,
		0, 0, 2 / (near - far), 0,
		0, 0, 0, 1;

	translate << 1, 0, 0, -(right + left) / 2,
		0, 1, 0, -(top + bottom) / 2,
		0, 0, 1, -(near + far) / 2,
		0, 0, 0, 1;

	persp2ortho << near, 0, 0, 0,
		0, near, 0, 0,
		0, 0, near + far, -near * far,
		0, 0, 1, 0;

	projection = scale * translate * persp2ortho;

	return projection;
}

绘制结果

简单的思考

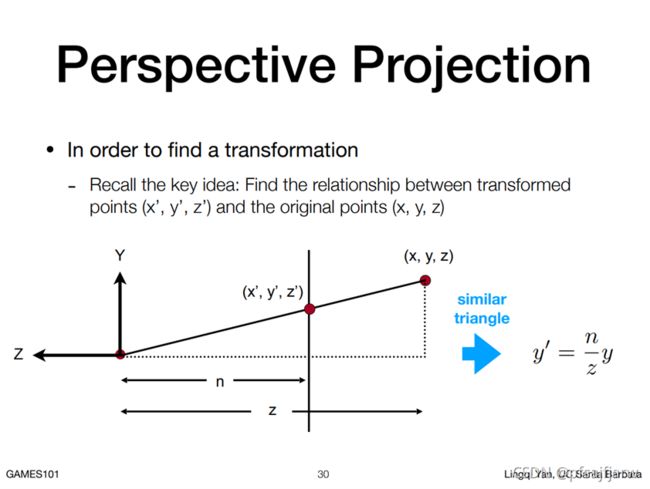
一开始的时候我画出的三角形，x轴和y轴和上图是反的。看了一些其他同学的博文，也是反的，原因是在用$n$和$l$进行计算时，我们都直接用的是函数传进来的$zNear$和$zFar$，打印出来看这个值是正的。而$n$和$l$作为近远平面真实的z值，应该是负的。看下面这张课件应该能说明问题。所以对用来计算的near和far进行了取负值。