cs224w（图机器学习）2021冬季课程学习笔记7 Graph Neural Networks 1: GNN Model

诸神缄默不语-个人CSDN博文目录
cs224w（图机器学习）2021冬季课程学习笔记集合

YouTube 视频观看地址1 视频观看地址2 视频观看地址3
本章的视频没有PPT中有的第4部分（即 Graph Convolutional Networks and GraphSAGE 这一部分），但本文还是写了。

---

本章主要内容：
介绍深度学习基础。

介绍GNN思想：聚合邻居信息。
每一层都产生一种节点嵌入。将上一层的邻居信息聚合起来，连接本节点上一层信息，产生新的节点嵌入。
第一层节点嵌入就是节点特征。
GCN：用平均值作为聚合函数。
GraphSAGE：用各种聚合函数。

---

1. Graph Neural Networks 1: GNN Model

1. 回忆一下节点嵌入¹任务。其目的在于将节点映射到d维向量，使得在图中相似的节点在向量域中也相似。
   我们已经学习了 “Shallow” Encoding 的方法来进行映射过程，也就是使用一个大矩阵直接储存每个节点的表示向量，通过矩阵与向量乘法来实现嵌入过程。
   这种方法的缺陷在于：
   1. 需要 $O\left(|V|\right)$ 复杂度（矩阵的元素数，即表示向量维度d×节点数|V| ）的参数，太多了
      节点间参数不共享，每个节点的表示向量都是完全独特的
   2. transductive²：无法获取在训练时没出现过的节点的表示向量
   3. 无法应用节点特征信息
      
2. 本节课将介绍deep graph encoders，也就是用图神经网络GNN来进行节点嵌入。
   映射函数，即之前¹讲过的node embedding中的encoder：$ENC\left(v\right)=$ 基于图结构的多层非线性转换
   （对节点相似性的定义仍然可以使用之前Lecture 3¹中的DeepWalk、node2vec等方法）
3. 一个GNN网络的结构如图：
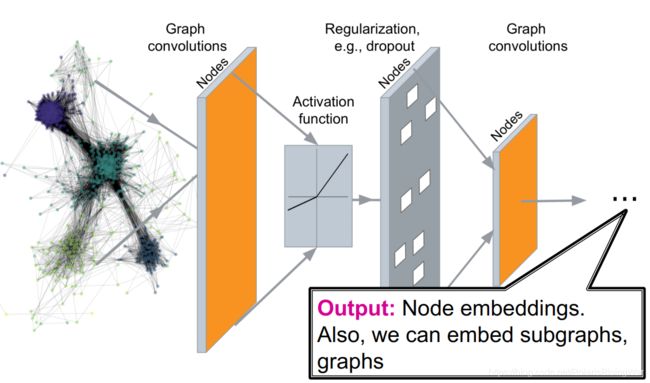
4. 通过网络可以解决的任务有：
   1. 节点分类：预测节点的标签
   2. 链接预测：预测两点是否相连
   3. 社区发现：识别密集链接的节点簇
   4. 网络相似性：度量图/子图间的相似性
5. 传统机器学习难以应用在图结构上。具体原因在Lecture 1中已经讲过，我也撰写过相应笔记³，不再赘述。

2. Basics of Deep Learning

1. 机器学习：一个优化任务
   有监督学习：输入自变量 $x$，预测标签 $y$
   
   将该任务视作一个优化问题：$\underset{\Theta }{\min }\mathcal{L}\left(y,f\left(x\right)\right)$
   $\Theta$ 是参数集合，优化对象，可以是一至多个标量、向量或矩阵。如在shallow encoder中 $\Theta =\{Z\}$（就是embedding lookup，那个大矩阵）。
   目标函数/损失函数：$\mathcal{L}$
   1. 举例：L2 loss（回归任务）：$\mathcal{L}\left(y,f\left(x\right)\right)=||y-f(x)|{|}_2$
   2. 其他常见损失函数：L1 loss、huber loss、max margin（hinge loss）、交叉熵（后文将详细介绍）……等。参考PyTorch官方文档：https://pytorch.org/docs/stable/nn.html#loss-functions
      
2. 损失函数举例：常用于分类任务的交叉熵cross entropy
   标签y是一个独热编码（所属类别索引的元素为1，其他元素为0）的分类向量
   如 $y=[0,0,1,0,0]$
   
   输出结果$f\left(x\right)$是经过softmax的概率分布向量，即 $f\left(x\right)=\text{Softmax}\left(g\left(x\right)\right)$⁴
   如 $f\left(x\right)=[0.1,0.3,0.4,0.1,0.1]$
   
   $\text{CE}\left(y,f\left(x\right)\right)=-{\sum }_{i=1}^C\left(y_i\log f{\left(x\right)}_i\right)$（C是类别总数，下标 $i$ 代表向量中第i个元素）
   CE越低越好，越低说明预测值跟真实值越近
   在所有训练集数据上的总交叉熵：$\mathcal{L}={\sum }_{(x,y)\in \mathrm{T}}\text{CE}\left(y,f\left(x\right)\right)$（$\mathrm{T}$ 是所有训练集数据）
3. 梯度向量 ${\nabla }_{\Theta }\mathcal{L}$：函数增长最快的方向和增长率，每个元素是对应参数在损失函数上的偏微分。
   方向导数：函数在某个给定方向上的变化率。
   梯度是函数增长率最快的方向的方向导数。⁵
4. 梯度下降
   迭代：将参数向梯度负方向更新：$\Theta \leftarrow \Theta -\eta {\nabla }_{\Theta }\mathcal{L}$（直至收敛）
   学习率learning rate $\eta$ 是一个需要设置的超参数，控制梯度下降每一步的步长，可以在训练过程中改变（有时想要学习率先快后慢：LR scheduling）
   理想的停止条件是梯度为0，在实践中一般则是用“验证集上的表现不再提升”作为停止条件。（据我的经验一般是设置最大迭代次数，如果在验证集上表现不再增加就提前停止迭代（early stopping））
5. 随机梯度下降stochastic gradient descent (SGD)
   每一次梯度下降都需要计算所有数据集上的梯度，耗时太久，因此我们使用SGD的方法，将数据分成多个minibatch，每次用一个minibatch来计算梯度。
6. minibatch SGD
   SGD是梯度的无偏估计，但不保证收敛，所以一般需要调整学习率。
   对SGD的改进优化器：Adam，Adagrad，Adadelta，RMSprop……等
   术语：
   1. batch size：每个minibatch中的数据点数
   2. iteration：在一个minibatch上做一次训练
   3. epoch：在整个数据集上做一次训练（在一个epoch中iteration的数量是 $\frac{dataset\_size}{batch\_size}$）
7. 神经网络函数
   目标函数：$\underset{\Theta }{\min }\mathcal{L}\left(y,f\left(x\right)\right)$
   深度学习中的 $f$ 可能非常复杂，为了简化，先假设一个线性函数：$f\left(x\right)=W\cdot x$（$\Theta =\{W\}$）
   如果 $f$ 返回一个标量，则 $W$ 是一个可学习的向量：${\nabla }_{W}f=(\frac{\partial f}{\partial w_1},\frac{\partial f}{\partial w_2},\frac{\partial f}{\partial w_1}...)$
   如果 $f$ 返回一个向量，则 $W$ 是权重矩阵：${\nabla }_{W}f=W^T$（$f$ 的雅克比矩阵⁶）
8. 反向传播
   对更复杂的函数，如 $f\left(x\right)=W_2\left(W_{1}x\right)$（$\Theta =\{W_1,W_2\}$）
   将该函数视为：$h\left(x\right)=W_{1}x$, $f\left(h\right)=W_{2}h$
   应用链式法则计算梯度：${\nabla }_{x}f=\frac{\partial f}{\partial h}\cdot \frac{\partial h}{\partial x}=\frac{\partial f}{\partial \left(W_{1}x\right)}\cdot \frac{\partial \left(W_{1}x\right)}{\partial x}$
   反向传播就是应用链式法则反向计算梯度，最终得到 $\mathcal{L}$ 关于参数的梯度。
9. 神经网络举例：简单两层线性网络 $f\left(x\right)=g\left(h\left(x\right)\right)=W_2\left(W_{1}x\right)$
   在一个minibatch上的 L2 loss：${\mathcal{L}}_{(x,y)\in \mathcal{B}}=||y-f(x)|{|}_2$
   隐藏层：$x$ 的中间表示向量
     这里我们用 $h\left(x\right)=W_{1}x$ 来表示隐藏层
     $f\left(x\right)=W_{2}h\left(x\right)$
   前向传播：从输入计算输出，用输出计算loss
   反向传播，计算梯度：
     $\frac{\partial \mathcal{L}}{\partial W_2}=\frac{\partial \mathcal{L}}{\partial f}\cdot \frac{\partial f}{\partial W_2}$
     $\frac{\partial \mathcal{L}}{\partial W_1}=\frac{\partial \mathcal{L}}{\partial f}\cdot \frac{\partial f}{\partial W_2}\cdot \frac{\partial W_2}{\partial W_1}$
10. 非线性
    ReLU：$ReLU\left(x\right)=\max \left(x,0\right)$
    Sigmoid：$\sigma \left(x\right)=\frac{1}{1+e^{-x}}$
11. 多层感知器Multi-layer Perceptron (MLP)
    MLP每一层都是线性转换和非线性结合：$x^{\left(l+1\right)}=\sigma \left(W_l{x}^{(l)}+b^l\right)$
12. 总结

3. Deep Learning for Graphs

1. 本节内容：
   1. local network neighborhoods
      1. 聚合策略
      2. 计算图
   2. 叠层
      1. 模型、参数、训练
      2. 如何学习？
      3. 无监督和有监督学习举例
2. Setup
   图 $G$
   节点集 $V$
   邻接矩阵 $\mathbf{A}$（二元，无向无权图。这些内容都可以泛化到其他情况下）
   节点特征矩阵 $\mathbf{X}\in {\mathbb{R}}^{m\times |V|}$
   一个节点 $v$
   $v$ 的邻居集合 $N(v)$
   如果数据集中没有节点特征，可以用指示向量indicator vectors（节点的独热编码）⁷，或者所有元素为常数1的向量。有时也会用节点度数来作为特征。
3. 我们可能很直接地想到，将邻接矩阵和特征合并在一起应用在深度神经网络上（如图，直接一个节点的邻接矩阵+特征合起来作为一个观测）。这种方法的问题在于：
   1. 需要 $O(|V|)$ 的参数
   2. 不适用于不同大小的图
   3. 对节点顺序敏感（我们需要一个即使改变了节点顺序，结果也不会变的模型）
4. Idea: 将网格上的卷积神经网络泛化到图上，并应用到节点特征数据
5. 图上无法定义固定的locality或滑动窗口，而且图是permutation invariant⁸的（节点顺序不固定）
6. 从image到graph：聚合邻居信息
   过程：转换邻居信息 $W_i{h}_i$，将其加总 ${\sum }_i{W}_i{h}_i$
7. Graph Convolutional Networks⁹
   通过节点邻居定义其计算图，传播并转换信息，计算出节点表示（可以说是用邻居信息来表示一个节点）
8. 核心思想：通过聚合邻居来生成节点嵌入
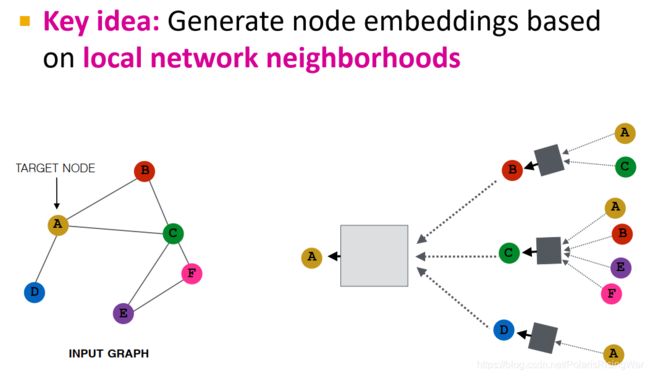
   直觉：通过神经网络聚合邻居信息
   直觉：通过节点邻居定义计算图（它的邻居是子节点，子节点的邻居又是子节点们的子节点……）
9. 深度模型就是有很多层。
   节点在每一层都有不同的表示向量，每一层节点嵌入是邻居上一层节点嵌入再加上它自己（相当于添加了自环）的聚合。
   第0层是节点特征，第k层是节点通过聚合k hop邻居所形成的表示向量。
   在这里就没有收敛的概念了，直接选择跑有限步（k）层。
10. 邻居信息聚合neighborhood aggregation
    不同聚合方法的区别就在于如何跨层聚合邻居节点信息（这是什么废话）。neighborhood aggregation方法必须要order invariant或者说permutation invariant⁸。
    基础方法：从邻居获取信息求平均，再应用神经网络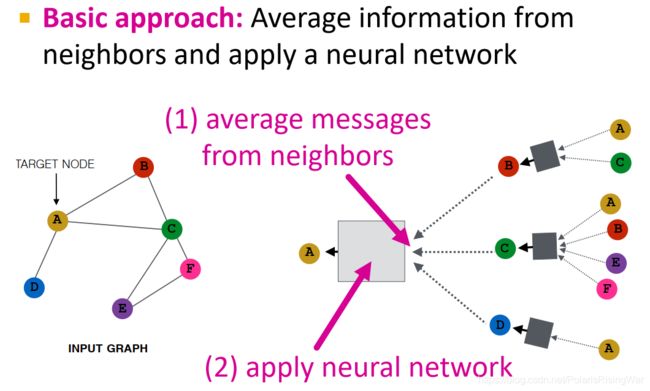
    这种deep encoder的数学公式：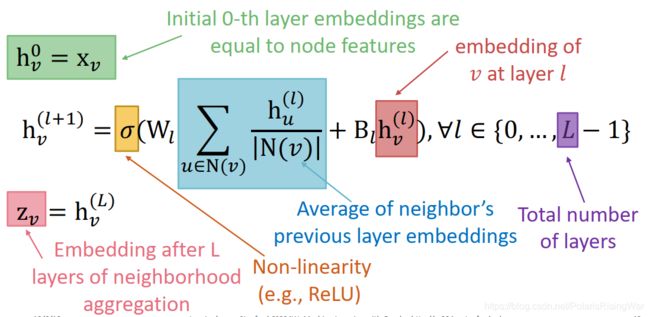
11. 如何训练模型：需要定义节点嵌入上的损失函数
12. $h_v^l$ 是 $l$ 层 $v$ 的隐藏表示向量。
    模型上可以学习的参数有 $W_l$（neighborhood aggregation的权重）和 $B_l$（转换节点自身隐藏向量的权重）（注意，每层参数在不同节点之间是共享的）。
    可以通过将输出的节点表示向量输入损失函数中，运行SGD来训练参数。
13. 矩阵形式
    很多种聚合方式都可以表示为（稀疏）矩阵操作的形式，如这个基础方法可以表示成图中这种形式：
    我自己写了个求解过程（因为线性代数比较差所以没法直接看出来怎么算的，得一点点推）
    补充：向量点积/矩阵乘法就是逐元素相乘然后累加，对邻接矩阵来说相当于对存在边的元素累加
    对整个公式的矩阵化也可以实现：
    这样就可以应用有效的稀疏矩阵操作（这部分我不了解，还没看）。
    同时，也要注意，当aggregation函数过度复杂时，GNN可能无法被表示成矩阵形式。
    
    （W和B要转置后放到右边，应该是因为矩阵尺寸的方向问题？（上一层嵌入维度×下一层嵌入维度））
14. 如何训练GNN
    节点嵌入 ${\mathbf{z}}_v$
    1. 有监督学习：优化目标 $\underset{\Theta }{\min }\mathcal{L}(\mathbf{y},f({\mathbf{z}}_v))$
       1. 如回归问题可以用L2 loss，分类问题可以用交叉熵
       2. 比如二分类交叉熵：$\mathcal{L}=-\sum _{v\in V}(y_v\log (\sigma (z_v^T\theta ))+(1-y_v)\log (1-\sigma (z_v^T\theta )))$（PPT中没有负号大概是写错了）
          1. $z_v$ 是encoder输出的节点嵌入向量
          2. 对于这个乘 $\theta$……我没搞懂classification weight是什么，感觉看起来像是把 $z_v^T$ 拉成标量的做法？
          3. 这个式子中，前后两个加数只有一个会被用到（y要么是1要么是0嘛）
    2. 无监督学习：用图结构作为学习目标
       1. 比如节点相似性（随机游走、矩阵分解、图中节点相似性……等）
       2. $\mathcal{L}=\sum _{z_u,z_v}\text{CE}(y_{u,v},\text{DEC}(z_u,z_v))$
          1. 如果 $u$ 和 $v$ 相似，则 $y_{u,v}=1$
          2. CE是交叉熵
          3. DEC是节点嵌入的decoder（如内积）¹
             
15. 模型设计：overview
    1. 定义邻居聚合函数
    2. 定义节点嵌入上的损失函数
    3. 在节点集合（如计算图的batch）上做训练
    4. 训练后的模型可以应用在训练过与没有训练过的节点上
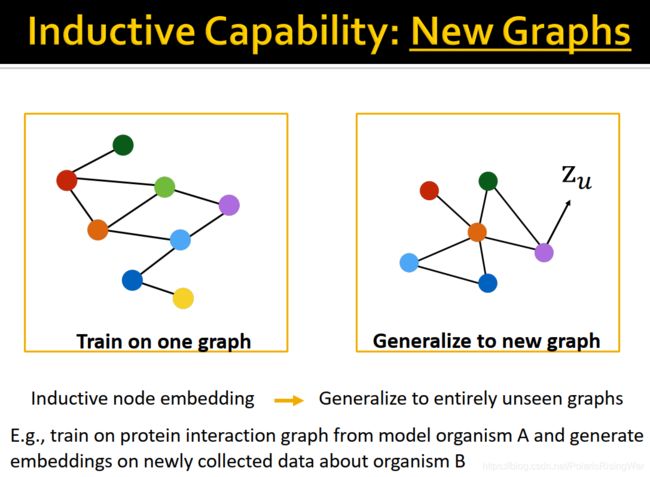
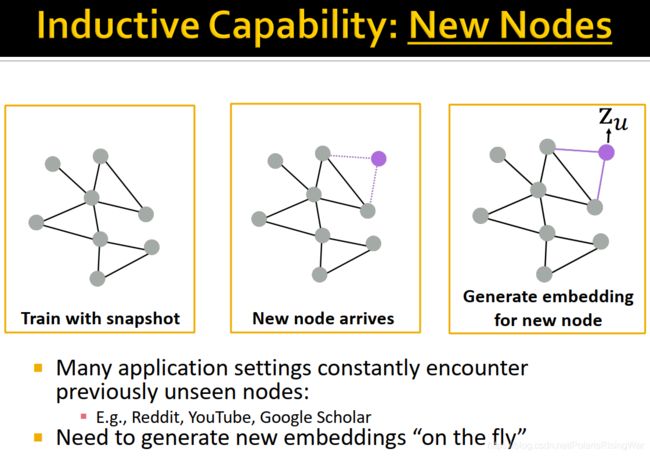
16. inductive² capability
    因为聚合邻居的参数在所有节点之间共享，所以训练好的模型可以应用在没见过的节点/图上。比如动态图就有新增节点的情况。
    模型参数数量是亚线性sublinear¹⁰于 $|V|$ 的（仅取决于嵌入维度和特征维度）（矩阵尺寸就是下一层嵌入维度×上一层嵌入维度，第0层嵌入维度就是特征维度嘛）。
17. 总结
    通过聚合邻居信息产生节点嵌入，本节阐述了这一总思想下的一个基本变体。具体GNN方法的区别在于信息如何跨层聚合。
    接下来讲GraphSAGE。

4. Graph Convolutional Networks and GraphSAGE

1. GraphSAGE¹¹
   这个聚合函数可以是任何将一组向量（节点邻居的信息）映射到一个向量上的可微函数：$h_v^{(l+1)}=\sigma ([W_l\cdot AGG(\{h_u^{(l)},\forall u\in N(v)\}),B_l{h}_v^{(l)}])$
   aggregation变体：
     1. Mean：$AGG=\sum _{u\in N(v)}\frac{h_u^{(l)}}{|N(v)|}$
     2. Pool：$AGG=\gamma (\{MLP(h_u^{(l)}),\forall u\in N(v)\})$（对邻居信息向量做转换，再应用对称向量函数¹²）
     3. LSTM：$AGG=LSTM([h_u^{(l)},\forall u\in \pi (N(v))])$（在reshuffle的邻居上应用LSTM）
   在每一层的节点嵌入上都可以做L2归一化：$h_v^k\leftarrow \frac{h_v^k}{||h_v^k|{|}_2}$（有时可以提升模型效果）
   
2. GCN vs. GraphSAGE
   核心思想：基于local neighborhoods产生节点嵌入，用神经网络聚合邻居信息
   GCN：邻居信息求平均，叠网络层
   GraphSAGE：泛化neighborhood aggregation所采用的函数

5. 总结

本节课中介绍了：

1. 神经网络基础：损失函数loss，优化optimization，梯度gradient，随机梯度下降SGD，非线性non-linearity，多层感知器MLP
2. 图深度学习思想
   1. 多层嵌入转换
   2. 每一层都用上一层的嵌入作为输入
   3. 聚合邻居和本身节点
3. GCN Graph Convolutional Network：用求平均的方式做聚合，可以用矩阵形式来表示
4. GraphSAGE：更有弹性的聚合函数

---

1. 我之前写的节点嵌入部分课程笔记：cs224w（图机器学习）2021冬季课程学习笔记3: Node Embeddings_诸神缄默不语的博客-CSDN博客 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

2. transductive：无法将模型泛化到训练时没有出现的数据上，在训练时就要应用全部训练集和测试集（举例：shallow encoding¹）
   inductive：在训练集上训练模型，模型可以用以预测在训练时没有出现过的测试集的数据（举例：本文中所讲的GNN，MLP等一般模型）
   参考资料：如何理解 inductive learning 与 transductive learning? - 知乎 ↩︎ ↩︎

3. cs224w（图机器学习）2021冬季课程学习笔记1 Introduction； Machine Learning for Graphs_诸神缄默不语的博客-CSDN博客 ↩︎

4. softmax介绍见Lecture 3（可参考¹），$f{\left(x\right)}_i=\frac{e^{g{\left(x\right)}_i}}{{\sum }_{j=1}^C{e}^{g{\left(x\right)}_j}}$（C是类别总数，下标 $i$ 代表向量中第i个元素） ↩︎

5. 方向导数的定义及其与梯度的关系
   参考资料：
   ①方向导数与梯度（Directional Derivatives and The Gradient） 
   ②方向导数(Directional derivatives) （有方向导数不一定有梯度）
   ③导数、微分、偏导数、全微分、方向导数、梯度的定义与关系
   ④函数的梯度方向和切线方向_方向导数和梯度是什么？ ↩︎

6. 雅克比矩阵是这个：
   
   形式其实还挺明确的……但是具体是干啥的我还没了解…… ↩︎

7. 这种方式的示例就是PyG包处理Zachary‘s karate club network节点特征：x = torch.eye(G.number_of_nodes(), dtype=torch.float)（来源：torch_geometric.datasets.karate — pytorch_geometric 1.7.0 documentation） ↩︎

8. permutation invariant 置换不变性：不假设特征之间有任何空间上的关系，特征调换顺序后结果不变，比如 $f((x_1,x_2,x_3))=f((x_2,x_1,x_3))=f((x_3,x_1,x_2))$。像加法这种交换律。MLP就是 permutation invariant 的，即使改变像素也不会改变结果；但是CNN就不行。（参考：machine learning - What does “permutation invariant” mean in the context of neural networks doing image recognition? - Cross Validated）
   在图上来说就是节点顺序与结果无关，是可以更换节点顺序的。
   参考资料：
   ①图深度学习：成果、挑战和未来 - 知乎
   ②Graph Neural Networks and Permutation invariance | by Michael Larionov, PhD | Towards Data Science 上一篇文章的原文。 ↩︎ ↩︎

9. Kipf, T., & Welling, M. (2017). Semi-Supervised Classification with Graph Convolutional Networks. ArXiv, abs/1609.02907. ↩︎

10. sublinear次线性的，亚线性的。就我看了一下觉得意思差不多就是复杂度比线性还低。
    参考资料：
    ①sublinear次线性复杂度是什么？
    ②请问什么叫做“亚线性”，什么又叫做“超线性”？ ↩︎

11. Hamilton, W.L., Ying, Z., & Leskovec, J. (2017). Inductive Representation Learning on Large Graphs. NIPS.
    这在arxiv上还显示有篇博文：How to do Deep Learning on Graphs with Graph Convolutional Networks | by Tobias Skovgaard Jepsen | Towards Data Science ↩︎

12. symmetric function对称函数，英文维基百科释义的翻译：在数学中，对于一个具有n个变量的函数，如果无论其参数顺序如何，其值都相同，则该函数是对称的。 ↩︎