人工智能实验1-波士顿房价预测
人工智能实验1-波士顿房价预测
- 1 实验内容
-
- 1.1 波士顿房价预测任务
- 1.2 线性回归模型
- 2 源代码
-
- 2.1 数据处理
-
- 2.1.1 读入数据
- 2.1.2 数据形状变换
- 2.1.3 数据集划分
- 2.1.4 数据归一化处理
- 2.1.5 封装成load data函数
- 2.2 模型设计
- 2.3 loss梯度可视化
- 2.4 用numpy求梯度
- 2.5、完整代码
- 3 运行结果
-
- 3.1 Loss 3D图
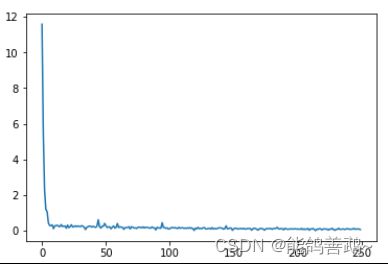
- 3.2 loss随训练次数变化
- 3.3 Loss的变化趋势
1 实验内容
1.1 波士顿房价预测任务
波士顿房价预测是一个经典的机器学习任务,类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同,波士顿地区的房价是由诸多因素影响的。该数据集统计了13种可能影响房价的因素和该类型房屋的均价,期望构建一个基于13个因素进行房价预测的模型,如 图1 所示。
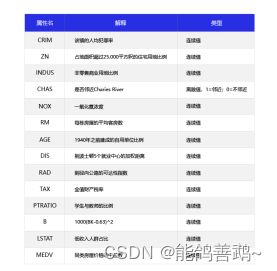
图1:波士顿房价影响因素示意图
对于预测问题,可以根据预测输出的类型是连续的实数值,还是离散的标签,区分为回归任务和分类任务。因为房价是一个连续值,所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题,并用神经网络来实现这个模型。
1.2 线性回归模型
模型的求解即是通过数据拟合出每个wj和b。其中,wj和b分别表示该线性模型的权重和偏置。一维情况下,wj和b是直线的斜率和截距。
线性回归模型使用均方误差作为损失函数(Loss),用以衡量预测房价和真实房价的差异,公式如下:
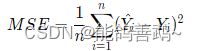
2 源代码
2.1 数据处理
#数据处理部分,共有五个步骤
2.1.1 读入数据
#导入需要用到的package
import numpy as np
import json
#读入训练数据
datafile = ‘./work/housing.data’
data = np.fromfile(datafile, sep=’ ')
#print(data)
2.1.2 数据形状变换
#读入之后的数据被转化成1维array,其中array的第0-13项是第一条数据,第14-27项是第二条数据,以此类推…
#这里对原始数据做reshape,变成N x 14的形式
feature_names = [ ‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’ , ‘DIS’ , ‘RAD’, ‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’, ‘MEDV’ ]
feature_num = len(feature_names)
#print(feature_num) # feature_num=14
data = data.reshape([data.shape[0] // feature_num, feature_num])
#print(data.shape) # (506, 14)
#print(data[0]) # 对应数据集第一行14个数据
2.1.3 数据集划分
ratio = 0.8 # 所有数据中作为训练集的比例
offset = int(data.shape[0] * ratio)
training_data = data[:offset] # 切片操作,从第0个到offset-1个
#print(training_data.shape) # (404, 14)
2.1.4 数据归一化处理
#计算train数据集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), training_data.sum(axis=0) / training_data.shape[0]
#print(maximums,minimums,avgs) 得到每一列的最大值、最小值、平均值
#对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i]) # 所有的值都在0-1之间了
2.1.5 封装成load data函数
#封装成函数的目的是方便以后的模型调用
def load_data():
# 从文件导入数据
datafile = ‘./work/housing.data’
data = np.fromfile(datafile, sep=’ ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ ‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’,
‘DIS’, ‘RAD’, ‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’, ‘MEDV’ ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0),
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
#获取数据
training_data, test_data = load_data()
x = training_data[:, :-1] # 去掉最后一列数据,每组数据变成13个
y = training_data[:, -1:] # 最后一列数据
2.2 模型设计
#模型设计
#将计算预测输出的过程以类和对象的方式来描述,类成员有w和b
class Network(object):
def init(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,
# 此处设置固定的随机数种子
np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
cost = error * error
cost = np.mean(cost)
return cost
2.3 loss梯度可视化
#固定w0-w12中除了w5和w9以外的参数,绘制loss关于w5和w9的三维图
net = Network(13)
losses = []
#只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值
w5 = np.arange(-160.0, 160.0, 1.0)
w9 = np.arange(-160.0, 160.0, 1.0)
losses = np.zeros([len(w5), len(w9)])
#计算设定区域内每个参数取值所对应的Loss
for i in range(len(w5)):
for j in range(len(w9)):
net.w[5] = w5[i]
net.w[9] = w9[j]
z = net.forward(x)
loss = net.loss(z, y)
losses[i, j] = loss
#使用matplotlib将两个变量和对应的Loss作3D图
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
w5, w9 = np.meshgrid(w5, w9)
ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap=‘rainbow’)
plt.show()
2.4 用numpy求梯度
#用numpy求梯度
#numpy具有广播机制(对向量和矩阵计算如同对1个单一变量计算一样),可以更快速的实现梯度计算
x1 = x[0]
y1 = y[0]
net = Network(13)
z1 = net.forward(x1)
gradient_w = (z1 - y1) * x1
print(‘gradient_w_by_sample1 {}, gradient.shape {}’.format(gradient_w, gradient_w.shape)) # 直接得到w0-w12共13个梯度
#一次想要计算多个样本的对梯度的影响的时候,可以利用Numpy的矩阵操作来简化运算
#注意这里是一次取出3个样本的数据,不是取出第3个样本
x3samples = x[0:3]
y3samples = y[0:3]
net = Network(13)
z3samples = net.forward(x3samples)
print(‘x {}, shape {}’.format(x3samples, x3samples.shape))
print(‘y {}, shape {}’.format(y3samples, y3samples.shape))
print(‘z {}, shape {}’.format(z3samples, z3samples.shape))
gradient_w = (z3samples - y3samples) * x3samples
print(‘gradient_w {}, gradient.shape {}’.format(gradient_w, gradient_w.shape))
#利用numpy的广播功能计算所有的样本的梯度
net = Network(13)
z = net.forward(x)
gradient_w = (z - y) * x
print(‘gradient_w shape {}’.format(gradient_w.shape)) # gradient_w shape (404, 13)
print(gradient_w)
#所有样本进入一次网络得到的关于w的梯度(包括最后的数据格式转换)
z = net.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_w
#计算所有样本进入网络一次b的梯度
gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
#此处b是一个数值,所以可以直接用np.mean得到一个标量
gradient_b
2.5、完整代码
#导入需要用到的package
import numpy as np
import json
import matplotlib.pyplot as plt
def load_data():
# 从文件导入数据
datafile = ‘D:\PycharmProjects\pytorch学习\波士顿房价预测\housing.data’
data = np.fromfile(datafile, sep=’ ')
# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数
feature_names = [ ‘CRIM’, ‘ZN’, ‘INDUS’, ‘CHAS’, ‘NOX’, ‘RM’, ‘AGE’, ‘DIS’, ‘RAD’, ‘TAX’, ‘PTRATIO’, ‘B’, ‘LSTAT’, ‘MEDV’ ]
feature_num = len(feature_names)
# 将原始数据进行Reshape,变成[N, 14]这样的形状
data = data.reshape([data.shape[0] // feature_num, feature_num])
# 将原数据集拆分成训练集和测试集
# 这里使用80%的数据做训练,20%的数据做测试
# 测试集和训练集必须是没有交集的
ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
# 计算训练集的最大值,最小值,平均值
maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0),
training_data.sum(axis=0) / training_data.shape[0]
# 对数据进行归一化处理
for i in range(feature_num):
#print(maximums[i], minimums[i], avgs[i])
data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])
# 训练集和测试集的划分比例
training_data = data[:offset]
test_data = data[offset:]
return training_data, test_data
class Network(object):
def init(self, num_of_weights):
# 随机产生w的初始值
# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子
# np.random.seed(0)
self.w = np.random.randn(num_of_weights, 1)
self.b = 0.
def forward(self, x):
z = np.dot(x, self.w) + self.b
return z
def loss(self, z, y):
error = z - y
num_samples = error.shape[0]
cost = error * error
cost = np.sum(cost) / num_samples
return cost
def gradient(self, x, y):
z = self.forward(x)
N = x.shape[0]
gradient_w = 1. / N * np.sum((z - y) * x, axis=0)
gradient_w = gradient_w[:, np.newaxis]
gradient_b = 1. / N * np.sum(z - y)
return gradient_w, gradient_b
def update(self, gradient_w, gradient_b, eta=0.01):
self.w = self.w - eta * gradient_w
self.b = self.b - eta * gradient_b
def train(self, training_data, num_epochs, batch_size=10, eta=0.01):
n = len(training_data)
losses = []
for epoch_id in range(num_epochs):
# 在每轮迭代开始之前,将训练数据的顺序随机打乱
# 然后再按每次取batch_size条数据的方式取出
np.random.shuffle(training_data)
# 将训练数据进行拆分,每个mini_batch包含batch_size条的数据
mini_batches = [training_data[k:k + batch_size] for k in range(0, n, batch_size)]
for iter_id, mini_batch in enumerate(mini_batches):
# print(self.w.shape)
# print(self.b)
x = mini_batch[:, :-1]
y = mini_batch[:, -1:]
a = self.forward(x)
loss = self.loss(a, y)
gradient_w, gradient_b = self.gradient(x, y)
self.update(gradient_w, gradient_b, eta)
losses.append(loss)
print(‘Epoch {:3d} / iter {:3d}, loss = {:.4f}’.
format(epoch_id, iter_id, loss))
return losses
#获取数据
train_data, test_data = load_data()
#创建网络
net = Network(13)
#启动训练
losses = net.train(train_data, num_epochs=50, batch_size=100, eta=0.1)
#画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()