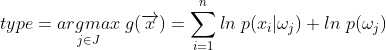实验——贝叶斯决策论预测贷款是否违约
目录
一 实验说明
1.1 背景
1.2 实验数据说明
1.3 实验注意事项
二 实验数据分析
三 实验原理
3.1 主要原理
3.2 处理分类数据
3.3 数据离散化
3.4 拉普拉斯平滑
四 代码实现
4.1 众数填充缺失值
4.2 处理分类数据
4.3 离散化
4.4 构造分类器
4.5 主函数与评估模型
五 实验结果
参考
一 实验说明
1.1 背景
信用风险是指银行向用户提供金融服务后,用户不还款的概率。信用风险一直是银行贷款决策中广泛研究的领域。信用风险对银行和金融机构,特别是商业银行来说,起着至关重要的作用,但是一直以来都比较难管理。
本实验以贷款违约为背景,要求使用贝叶斯决策论的相关知识在训练集上构建模型,在测试集上进行贷款违约预测并计算分类准确度。
1.2 实验数据说明
训练数据集train.csv包含9000条数据,测试数据集test.csv包含1000条数据。注意,训练集和测试集中都有缺失值存在。以下是字段说明:
| 字段 | 描述 |
|---|---|
| loan_id | 贷款记录唯一标识 |
| user_id | 借款人唯一标识 |
| total_loan | 贷款数额 |
| year_of_loan | 贷款年份 |
| interest | 当前贷款利率 |
| monthly_payment | 分期付款金额 |
| Grade/class | 贷款级别 |
| employment_type | 所在公司类型 |
| industry | 工作领域 |
| work_year | 工作年限 |
| home_exist | 是否有房 |
| censor_status | 审核情况 |
| issue_date | 贷款发放的月份 |
| use | 贷款用途类别 |
| post_code | 贷款人申请时邮政编码 |
| region | 地区编码 |
| debt_loan_ratio | 债务收入比 |
| del_in_18month | 借款人过去18个月逾期30天以上的违约事件数 |
| scoring_low | 借款人在贷款评分中所属的下限范围 |
| scoring_high | 借款人在贷款评分中所属的上限范围 |
| known_outstanding_loan | 借款人档案中未结信用额度的数量 |
| known_dero | 贬损公共记录的数量 |
| pub_dero_bankrup | 公开记录清除的数量 |
| recircle_bal | 信贷周转余额合计 |
| recircle_util | 循环额度利用率 |
| initial_list_status | 贷款的初始列表状态 |
| app_type | 是否个人申请 |
| earlies_credit_mon | 借款人最早报告的信用额度开立的月份 |
| title | 借款人提供的贷款名称 |
| policy_code | 公开可用的策略代码=1新产品不公开可用的策略代码=2 |
| f系列匿名特征 | 匿名特征f0-f4,为一些贷款人行为计数特征的处理 |
| early_return | 借款人提前还款次数 |
| early_return_amount | 贷款人提前还款累积金额 |
| early_return_amount_3mon | 近3个月内提前还款金额 |
| isDefault | 贷款是否违约(预测标签) |
1.3 实验注意事项
-
实验不限制使用何种高级语言,推荐使用python中pandas库处理csv文件。
-
在进行贝叶斯分类之前重点是对数据进行预处理操作,如,缺失值的填充、将文字表述转为数值型、日期处理格式(处理成“年-月-日”三列属性或者以最早时间为基准计算差值)、无关属性的删除等方面。
-
数据中存在大量连续值的属性,不能直接计算似然,需要将连续属性离散化。
-
另外,特别注意零概率问题,贝叶斯算法中如果乘以0的话就会失去意义,需要使用平滑技术。
-
实验目的是使用贝叶斯处理实际问题,不得使用现成工具包直接进行分类。
-
实验代码中需要有必要的注释。
二 实验数据分析
训练样本是没有预处理的数据,直接用来训练模型是不现实的,首先我们要进行数据的分析。
贷款记录唯一标识(loan_id)、借款人唯一标识(user_id)属于标志属性,与实际问题没有关联,可以删除。
贷款年份(year_of_loan)、贷款发放的月份(issue_date)、借款人最早报告的信用额度开立的月份(earlies_credit_mon)、贷款人申请时邮政编码(post_code)、地区编码(region)。这些时间地点属性对贷款人的还款行为没有过多影响,也可以剔除。【1】
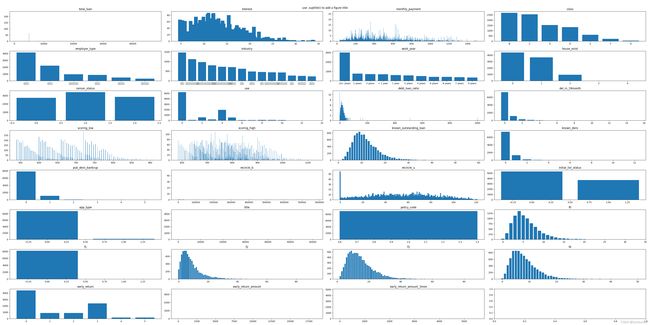
通过对剩下的字段画出频率分布直方图分析:
是否个人申请(app.type)、公开可用的策略(policy_code)、匿名特征(f1)属于归一化属性,即一个变量大部分的观测都是相同的特征,那么认为此类特征变量无法显著区分目标变量,可以考虑将其删除。
而工作领域(industry)、(贷款级别)class、(工作年限)work_year、(所在公司类型)employer_type,这些字段都是属于分类变量,需要进行分类处理。
同时字段total_loan、interest、monthly_payment、debt_loan_ratio、scoring_low、scoring_high、 recircle_b、recircle_u、early_return_amount_3mon的取值是连续值(小数),因此需要对这些数据进行离散化。特征离散化后,模型会更稳定,降低了模型过拟合的风险。
对于缺失的数据,可以利用众数填充。
三 实验原理
3.1 主要原理
本次实验原理主要为朴素贝叶斯决策论。什么是贝叶斯决策论可以看我的上一篇文章:
(3条消息) 贝叶斯决策论理论_Sunburst7的博客-CSDN博客
如果使用普通的贝叶斯方法计算后验概率时,类条件概率 ![]() 是特征向量
是特征向量 ![]() 上所有特征的联合概率,难以从有限的训练样本中直接得到。为了避开这个障碍,朴素贝叶斯分类器采用了属性条件独立性假设:对已知类别,假设所有属性相互独立,换言之,假设每个属性独立地对分类结果发生影响。基于这个假设,我们的后验概率可以修改为:【2】
上所有特征的联合概率,难以从有限的训练样本中直接得到。为了避开这个障碍,朴素贝叶斯分类器采用了属性条件独立性假设:对已知类别,假设所有属性相互独立,换言之,假设每个属性独立地对分类结果发生影响。基于这个假设,我们的后验概率可以修改为:【2】
对于特征向量中的每一个特征的条件概率容易计算 ![]() 去除相同的证据因子
去除相同的证据因子![]() ,再取对数,我们得到模型分类器:
,再取对数,我们得到模型分类器:
对于本实验的二分类问题,只要简单的比较两个类型的g(x)即可。
3.2 处理分类数据
有时候,根据某种特性而不是数量来度量对象会更有效。我们常常使用这种定性的信息来判断一个观察值的属性,比如按照性别、颜色或者车的品牌这样的类别对其分类。本身没有内在顺序的特征类别称为 nominal。分类的特征总是有某种天然顺序的称为ordinary。【3】
- 对于内部没有顺序的分类(性别,水果类型):通常使用one-hot编码
- 对于内部有顺序的分类(非常同意、同意、保持中立、反对..):将 ordinal 分类转换成数值,同时保留其顺序。最常见的方法就是,创建一个字典,将分类的字符串标签映射为一个数字,然后将 其映射在特征上。
本次实验中的class、industry、work_year、employer_type都属于分类特征,我们可以采用将特征值映射到一个数字的方法。
3.3 数据离散化
对于连续型的特征,在计算似然时很难找到同类型的数据,这样就会出现类条件概率为0的情况,使得分类器判别出现误差,为了避免这种情况,需要将连续特征离散化。这里用到的技术通常被称为数据分箱:【4】
常见的分箱方法主要分为有监督与无监督两种,本实验采用卡方分箱对数据离散化:
-
无监督分箱:不需要提供预测标签,仅凭借特征就能实现分箱
-
等宽分箱
-
等频分箱
-
-
有监督分箱:需要结合预测标签的值,通过算法实现分箱
-
决策树分箱
-
卡方分箱:关于卡方分箱的原理可以看参考【5】的博客
-
3.4 拉普拉斯平滑
计算要预测数据集的某个特征似然时,如果在观察样本库(训练集)中没有出现过,会导致类条件概率结果是0。在贝叶斯分类中如果乘以0的话,整个后验概率就会失去意义。
为了解决零概率的问题,法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加法平滑也叫做拉普拉斯平滑。假定训练样本很大时,每个分量x的计数加1造成的估计概率变化可以忽略不计,但可以方便有效的避免零概率问题。因此特征向量中某一个特征的类条件概率密度的计算公式可以改写为:
四 代码实现
4.1 众数填充缺失值
dataframe.isnull().any()返回一个Series,某行/列存在缺失值为True,axis=0表示跨行检测,即每一列跨行检测,返回一个与列等宽的Series
dataframe.fillna(value,inplace=True)表示用value填充DataFrame中NaN的数据,inplace=True表示填充内存中的DataFrame而不是副本。
# 按照众数填充缺失值
def fillMissingColumn(dataframe: pd.DataFrame):
# 检测出有缺失值的列,返回一个Series,有缺失值的列为True,无缺失值的列为False
missing_column = dataframe.isnull().any(axis=0) # 按列检测
for index, value in missing_column.items():
if value:
print(index + " needs to fill missing values")
# 利用众数填充有缺失值的行
dataframe[index].fillna(dataframe[index].mode()[0], inplace=True) # 一定要设置inplace=True 修改内存的值4.2 处理分类数据
将class(A,B,C,D,E)利用func函数映射到1-5。mapper定义了映射字典,将分类特征映射到对应的整数。最后利用dataframe.replace(dict)替换
# 处理nominal型的分类数据-industry:一共有14类 使用one-hot编码太大,还是采用简单编码
# 处理ordinary型的分类数据:employer_type class work_year
def classifyOrdinary(dataframe: pd.DataFrame):
# 创建class特征 映射器,将A-1,B-2...F-6
func = lambda x: ord(x) - 64 # ord()将字母转变为ASCII码
# 将class特征分类
dataframe['class'] = dataframe['class'].apply(func)
# 创建编码映射器
mapper = {
'industry': {
'金融业': 0,
'电力、热力生产供应业': 1,
'公共服务、社会组织': 2,
'住宿和餐饮业': 3,
'信息传输、软件和信息技术服务业': 4,
'文化和体育业': 5,
'建筑业': 6,
'房地产业': 7,
'采矿业': 8,
'交通运输、仓储和邮政业': 9,
'农、林、牧、渔业': 10,
'制造业': 11,
'批发和零售业': 12,
'国际组织': 13
},
'work_year': {
'< 1 year': 0,
'1 year': 1,
'2 years': 2,
'3 years': 3,
'4 years': 4,
'5 years': 5,
'6 years': 6,
'7 years': 7,
'8 years': 8,
'9 years': 9,
'10+ years': 10,
},
'employer_type': {
'普通企业': 1,
'幼教与中小学校': 2,
'政府机构': 3,
'上市企业': 4,
'高等教育机构': 5,
'世界五百强': 6
}
}
# 离散化
dataframe = dataframe.replace(mapper, inplace=True)4.3 离散化
参考【4】中的博客,利用scorecardpy包先计算出分箱区间:
import pandas as pd
import scorecardpy as sc
# 导入两列数据
df = pd.DataFrame({'年龄': [29,7,49,12,50,34,36,75,61,20,3,11],
'Y' : [0,0,1,1,0,1,0,1,1,0,0,0]})
bins = sc.woebin(df, y='Y', method='chimerge') # 卡方分箱
sc.woebin_plot(bins)使用np.digitize(DataFrame,bin:list)进行离散化
"""
连续的属性值无法计算似然(后验概率)!需要将其离散化——数据分箱
需要离散化的列有:total_loan、interest、monthly_payment、debt_loan_ratio、scoring_low、scoring_high、
recircle_b、recircle_u、early_return_amount_3mon、early_return_amount、title
参考博客:https://blog.csdn.net/Orange_Spotty_Cat/article/details/116485079
"""
def discretize(dataframe):
# 使用分箱技术
dataframe['total_loan'] = np.digitize(dataframe['total_loan'], bins=[8000, 21000, 24000, 31000])
# dataframe['interest'] = np.digitize(dataframe['interest'], bins=range(5, 36, 1)) # 4.779-33.979
dataframe['interest'] = np.digitize(dataframe['interest'], bins=[7, 9, 10, 12, 16, 21])
# dataframe['monthly_payment'] = np.digitize(dataframe['monthly_payment'], bins=range(100, 2000, 100)) # 30.44-1503.89
dataframe['monthly_payment'] = np.digitize(dataframe['monthly_payment'], bins=[250, 500])
# dataframe['debt_loan_ratio'] = np.digitize(dataframe['debt_loan_ratio'], bins=range(10, 1000, 10)) # 0-999
dataframe['debt_loan_ratio'] = np.digitize(dataframe['debt_loan_ratio'], bins=[11, 15, 26])
# dataframe['scoring_low'] = np.digitize(dataframe['scoring_low'], bins=range(10, 1000, 10)) # 540-910.9
dataframe['scoring_low'] = np.digitize(dataframe['scoring_low'], bins=[560, 600, 630, 660, 680, 780])
# dataframe['scoring_high'] = np.digitize(dataframe['scoring_high'], bins=range(10, 2000, 10)) # 585.0-1131.818182
dataframe['scoring_high'] = np.digitize(dataframe['scoring_high'], bins=[730, 750, 860])
# dataframe['recircle_b'] = np.digitize(dataframe['recircle_b'], bins=range(10000, 770000, 10000)) # 0.0-779021.0
dataframe['recircle_b'] = np.digitize(dataframe['recircle_b'], bins=[16000])
# dataframe['recircle_u'] = np.digitize(dataframe['recircle_u'], bins=range(1, 120, 1)) # 0.0-120.6153846
dataframe['recircle_u'] = np.digitize(dataframe['recircle_u'], bins=[38, 56, 66, 70])
# dataframe['early_return_amount_3mon'] = np.digitize(dataframe['early_return_amount_3mon'],bins=range(1, 5500, 10)) # 0.0-5523.9
dataframe['early_return_amount_3mon'] = np.digitize(dataframe['early_return_amount_3mon'], bins=[50, 150, 1250])
dataframe['title'] = np.digitize(dataframe['title'], bins=[1])
dataframe['early_return_amount'] = np.digitize(dataframe['early_return_amount'], bins=[5000,10000,15000,20000])4.4 构造分类器
为了避免大量重复的计算类条件概率(有很多特征取值相同,计算的类条件概率也是重复的),先用两个numpy的二维数据(利用下标访问)存储所有可能特征值的类条件概率。计算出还剩下29个特征,经过离散化后每个特征的取值类型在100种以内。初始化为0。
train.columns.get_loc(columns_label)用于返回某个列名的列索引值。
"""
朴素贝叶斯分类,假设每个字段之间相互独立:
小数的连乘可能下溢,因此对p(x|w)*p(w)取对数
为了防止零概率情况使log无意义,使用拉普拉斯平滑技术
定义一个分类器 g(x) = lnp(x|w)+lnp(w)
输入一个特征向量x与一个数据集,输出它的分类
"""
# 创建两个dataframe分别缓存isDefault=0与isDefault=1的似然值
storeage0 = np.zeros((29,100))
storeage1 = np.zeros((29,100))
def classifier(x, train: pd.DataFrame):
# 分别统计贷款没违约与贷款违约的情况
type0 = train[train['isDefault'] == 0]
type1 = train[train['isDefault'] == 1]
# 计算行数
sum_type0 = type0.count().values[0]
sum_type1 = type1.count().values[0]
# 计算先验概率
prior_0 = sum_type0 / (sum_type0 + sum_type1)
prior_1 = sum_type1 / (sum_type0 + sum_type1)
# print(str(prior_0) + " " + str(prior_1))
# 初始化分类器值(加上lnp(w))
g0 = math.log(prior_0)
g1 = math.log(prior_1)
# print(str(g0) + " " + str(g1))
# 计算所有列的似然/类条件概率密度
for column in train.columns:
if column != 'isDefault': # 去除预测标签的影响
likelihood0, likelihood1 = 0, 0
if storeage0[train.columns.get_loc(column)][int(x[column])] > 0:
# 缓存中已有数据
likelihood0 = storeage0[train.columns.get_loc(column)][int(x[column])]
else:
# 计算拉普拉斯平滑后的似然
likelihood0 = (type0[type0[column] == x[column]].count().values[0] + 1) / (
sum_type0 + train[column].nunique())
# 按照行-列索引,列—特征值 将数据保存在缓存中
storeage0[train.columns.get_loc(column)][int(x[column])] = likelihood0
# 对 isDefault = 1的训练集数据进行一次同样的操作,计算后验概率
if storeage1[train.columns.get_loc(column)][int(x[column])] > 0:
likelihood1 = storeage1[train.columns.get_loc(column)][int(x[column])]
else:
likelihood1 = (type1[type1[column] == x[column]].count().values[0] + 1) / (
sum_type1 + train[column].nunique())
storeage1[train.columns.get_loc(column)][int(x[column])] = likelihood1
# 取对数
ln_likelihood0 = math.log(likelihood0)
ln_likelihood1 = math.log(likelihood1)
# print("type0: likelihood: " + str(likelihood0) + " ln:" + str(ln_likelihood0))
# print("type1: likelihood: " + str(likelihood1) + " ln:" + str(ln_likelihood1))
g0 += ln_likelihood0
g1 += ln_likelihood1
# print('------------------------------------------------------------------')
# print(str(g0) + " " + str(g1))
if g0 >= g1:
# 预测为不违约
return 0
else:
return 14.5 主函数与评估模型
假设贷款不违约(isDefault=0)为正例,贷款违约(isDefault=1)为负例。利用正确率、精度、召回率评估模型。
# 读取训练集
trainSet = pd.read_csv('train.csv')
# 读取测试集
testSet = pd.read_csv('test.csv')
# 删除无关数据列(用户的id,贷款年份(year_of_loan)、贷款发放的月份(issue_date)、借款人最早报告的信用额度开立的月份(earlies_credit_mon)、贷款人申请时邮政编码(post_code)、地区编码(region)等信息,主观判断其对是否违约影响甚微。都是无关属性)
trainSet = trainSet.drop(
['year_of_loan', 'loan_id', 'user_id', 'earlies_credit_mon', 'issue_date', 'post_code', 'region'], axis=1)
testSet = testSet.drop(
['year_of_loan', 'loan_id', 'user_id', 'earlies_credit_mon', 'issue_date', 'post_code', 'region'], axis=1)
# 画出频率分布直方图分析数据
fig,axs=plt.subplots(8,4,figsize=(40,20),sharex=False,sharey=False)
for i in range(10):
for j in range(4):
if i*4+j<31:
axs[i][j].set_title(trainSet.columns[i*4+j])
axs[i][j].bar(x=pd.value_counts(trainSet[trainSet.columns[i*4+j]]).index,height=pd.value_counts(trainSet[trainSet.columns[i*4+j]]).values)
plt.show()
# 而app_type policy_code 与 f1都是归一化属性,直接去除
trainSet = trainSet.drop(['app_type', 'policy_code', 'f1'], axis=1)
testSet = testSet.drop(['app_type', 'policy_code', 'f1'], axis=1)
# 数据预处理
fillMissingColumn(trainSet)
classifyOrdinary(trainSet)
discretize(trainSet)
fillMissingColumn(testSet)
classifyOrdinary(testSet)
discretize(testSet)
# 保存分类器的分类结果
isDefault_f = []
for index, row in testSet.iterrows():
isDefault_f.append(classifier(row, trainSet))
# 将分类结果添加到测试集中
testSet['forecast'] = isDefault_f
# 创建评估数据集
evaluation = testSet[['isDefault', 'forecast']]
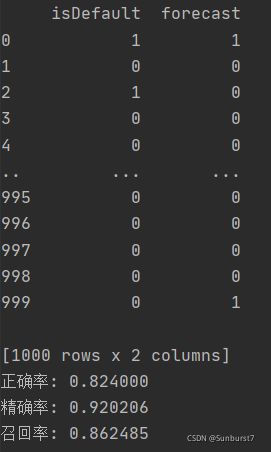
print(evaluation)
# 假设 没有违约(isDefault == 0)为正例
TP = 0 # 真正例
TN = 0 # 真负例
FP = 0 # 假正例
FN = 0 # 假负例
for index, row in evaluation.iterrows():
if row['isDefault'] == 0 and row['forecast'] == 0:
TP += 1
if row['isDefault'] == 0 and row['forecast'] == 1:
FN += 1
if row['isDefault'] == 1 and row['forecast'] == 0:
FP += 1
if row['isDefault'] == 1 and row['forecast'] == 1:
TN += 1
Accuracy = (TP + TN) / (TP + TN + FP + FN)
Precision = TP / (TP + FP)
Recall = TP / (TP + FN)
print("正确率: %f" % Accuracy)
print("精确率: %f" % Precision)
print("召回率: %f" % Recall)五 实验结果
测试集共有1000行数据,forecast为我们预测的数据。正确率还有待改进。
参考
【1】(3条消息) Lending Club贷款违约预测_Mango的博客-CSDN博客
【2】机器学习—周志华
【3】Python机器学习手册:从数据预处理到深度学习
【4】数据科学猫:数据预处理 之 数据分箱(Binning)_Orange_Spotty_Cat的博客-CSDN博客
【5】从论文分析,告诉你什么叫 “卡方分箱”? - 云+社区 - 腾讯云 (tencent.com)