深度学习-Tensorflow2.0实现全连接神经网络

1、数据和问题描述

  本文采用Tensorflow实现全连接神经网络，对鸢尾花数据进行分类。首先加载数据集，代码如下：

import tensorflow as tf
from sklearn import datasets
import numpy as np

# 读取数据
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

  数据集的特征包含4列，如下图所示：

  标签列的取值为（0，1，2）三种，是一个多分类问题。

2、数据预处理

  将数据集打乱顺序，并划分为训练集和测试集，代码如下：

# 用相同的随机种子打乱数据集
np.random.seed(116)
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)

tf.random.set_seed(116)

x_train = x_data[:-30]
y_train = y_data[:-30]

x_test = x_data[-30:]
y_test = y_data[-30:]

  这里查看一下 x_train 的数据类型：

x_train.dtype
# dtype('float64') #输出的类型是float64

  为了避免后续进行计算的时候出现数据类型不一致的情况，这里对 x_train、x_test 进行类型转换：

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

  将特征和标签配对，并划分为多个 batch，代码如下：

train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

3、构建网络模型

  构建一个3层的神经网络，包含2层全连接层。网络第1层激活函数为 Relu ，第2层激活函数为 Softmax ，网络结构如下图所示：

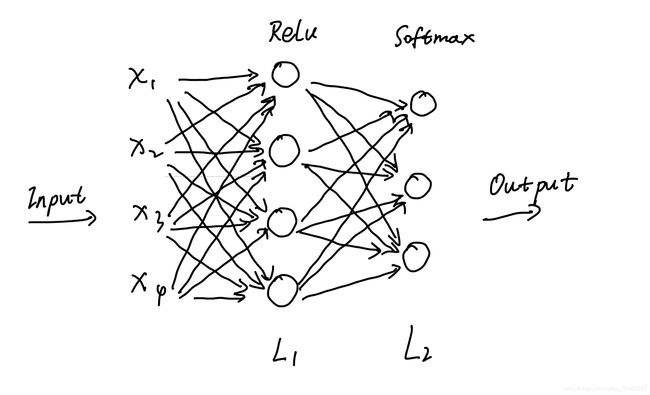
3.1

  按照网络结构，定义模型参数。代码如下：

w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

w2 = tf.Variable(tf.random.truncated_normal([3, 3], stddev=0.1, seed=1))
b2 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

  这里也看一下参数 w1 的数据类型，会发现参数类型是 float32，与上文中转换类型后的 x_train、x_test 的类型一致：

<tf.Variable 'Variable:0' shape=(4, 4) dtype=float32, numpy=
array([[ 0.08249953, -0.0683137 ,  0.19668601, -0.05480815],
       [ 0.04570521,  0.1357149 ,  0.07750896, -0.16734955],
       [-0.10294553,  0.15784004, -0.13311003,  0.06045313],
       [ 0.0198621 , -0.03865892, -0.02031356, -0.01440386]],
      dtype=float32)>

3.2

  定义构建网络过程中用到的参数，代码如下：

loss_all = 0	# 损失值
lr = 0.1		# 学习率
epoch = 500		# 训练网络时的迭代次数
total_correct = 0	#预测正确的样本数量

3.3

  接下来进行神经网络的训练，代码如下：

# 模型训练
for epoch in range(epoch):
    for step, (x_train, y_train) in enumerate(train_db): 
        with tf.GradientTape() as tape:
            
            # 计算第1层
            y_1 = tf.matmul(x_train, w1) + b1
            y_1 = tf.nn.relu(y_1)
            
            #计算第2层
            y = tf.matmul(y_1, w2) + b2
            y = tf.nn.softmax(y)
                
            y_ = tf.one_hot(y_train, depth=3)
            
            # 损失函数使用均方误差
            loss = tf.reduce_mean(tf.square(y - y_))
            print(loss)
                
            loss_all += loss.numpy()
        
        # 这里是对loss求导
        grads = tape.gradient(loss, [w1, b1, w2, b2])
        
        # 更新各个参数
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])
        w2.assign_sub(lr * grads[2])
        b2.assign_sub(lr * grads[3])
        
    print("Epoch {}, loss: {}".format(epoch, loss_all/4))

3.4

  用测试集对模型效果进行检验，代码如下：

# 模型预测
for x_test, y_test in test_db:
    y_1 = tf.matmul(x_test, w1) + b1
    y = tf.matmul(y_1, w2) + b2
    y = tf.nn.softmax(y)
    
    pred = tf.argmax(y, axis=1)
    pred = tf.cast(pred, dtype=y_test.dtype)
    correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
    correct = tf.reduce_sum(correct)
    total_correct += correct
    
acc = total_correct / y_test.shape[0]
print('test_acc', acc)

  打印模型预测的准确率：

acc.numpy()
#输出 1.0

参考连接：https://www.bilibili.com/video/BV1Cg4y1q7Xq?from=search&seid=15330922952568668566