Explainability in Graph Neural Networks:A Taxonomic Survey 图可解释
typora-root-url: img
Explainability in Graph Neural Networks:A Taxonomic Survey
可解释GNN的分类和数据集(句子==>图数据集)
对于 GNN 解释性方法,既没有一个统一的处理方法,也没有一个标准的基准测试和测试平台
首先,与图像和文本不同,图不是网格状的数据,这意味着没有局部信息,这意味着没有局部信息,每个节点有不同数量的邻居。没有位置信息,只有拓扑信息,且分布不均匀
图包含了重要的拓扑信息,并被表示为特征矩阵和邻接矩阵。Mask应用于邻接矩阵将破坏离散性
图像中可以,把输⼊视为可训练变量,通过反向传播优化输⼊以获得抽象图===>>>图中不能以相同方式优化离散的邻接矩阵
对于图像和文本----->像素或单词重要性
对于图------>结构信息更为重要(motif可能比节点还重要,尤其是分子图上)
图上的可解释模型一般都会回答一些问题:
哪些输入的边更重要?
哪个输入的节点更重要?
哪些节点特征更重要?
哪些motif将最大化某个类别的预测?
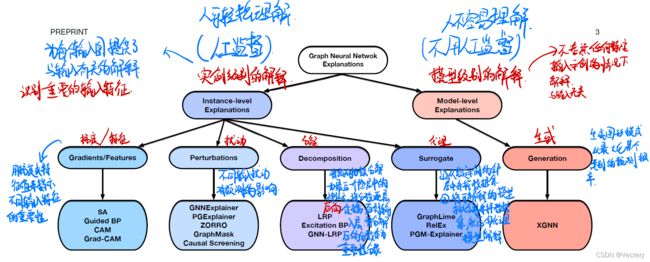
本文将常见的GNN可解释模型分为两个大类:实例级和模型级
梯度或特征
是最直接与模型参数高度相关的解释
主要思想是:使用梯度和隐藏特征map值作为输入的近似值,反向传播相对于输入特征的预测的梯度,将隐藏的特征映射到输入空间以测量重要性得分,较大的梯度或特征值表示较高的重要性
SA ∇ 2 \nabla^2 ∇2
直接采用梯度的平方值作为不同输入特征的重要性得分,可以通过反向传播直接计算,和训练网络一样,但目标是输入特征而不是模型参数,输入特征可以是图节点,边或者节点特征,假设较高的绝对梯度值指示相应的输入特征更加重要.
局限性:只能反应输入和输出之间的灵敏度,不能准确显示其重要性,而且在饱和区域,对于修改输入,梯度都无法反应
直接在input处构建squared value反应特征重要性,直接处理bp过程。缺陷在于SA仅反应了输入和输出的敏感性但重要性的准确性欠佳,其次,模型存在过饱和问题。
Guided BP
与SA有一样的想法,修改反向传播的过程,由于负梯度很难解释(负的不能说明他对结果起到是负作用)
因此负梯度再反向传播的过程中把负梯度都变为0,只有正的梯度用来衡量不同输入特征重要性.
CAM
将最后一层中的节点特征映射到输入空间以标识重要节点,需要GNN模型,采用g全局平局池化层 (GAP)和全连接层(FC)作为最后一层的分类器.通过加权求和并不同的特征图来获得输入节点的重要性分数,权重来自最终的全连接层与目标预测相关的图层
不能应用于节点分类任务
将最后一层节点特征映射至输入空间寻找重要信息。这种方法要求GNN需要兼顾全局信息并且最后是一个全连接分类器。这里实际上是假设了最后的节点embedding 反应了输入信息的重要性,这样就会比较模糊。然后这个模型仅能解释分类结果但不能用于分类任务。
Grad-CAM
取消了必须用GAP层的 约束,使用梯度作为权重进行组合不用特征图.
首先计算目标预测相对于最终目标梯度的节点嵌入,然后讲这些梯度求平均值,以获得每个特征图的权重
不能应用于节点分类任务
CAM模型的衍生,加入了GAP层对图分类进行约束。与CAM相似,也是去映射节点embedding。由于引进了GAP,所以相对CAM就不需要约束问题最后一层是一个全链接了。当然,这个模型的解释性依旧是模糊的。
基于扰动的方法
研究关于不同输入扰动输出的变化.
当保留了重要输入信息时,预测不变
这样的方法不能直接应用于图模型,图包含节点和边,他们无法调整大小以贡献相同的节点和边,而且结构信息对图形至关重要,可以确定特征.
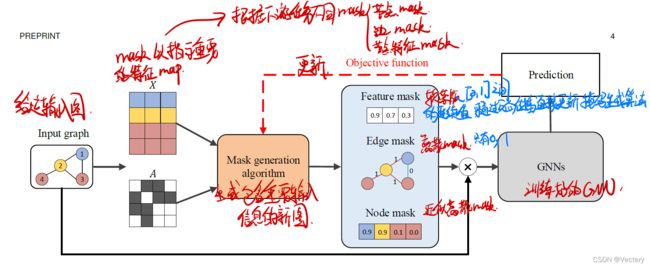
这些方法主要区别在Mask方法上:
软Mask:会引入非0,1的值,引入噪声,引入证据
离散Mask:只有0,1,输出的Mask不是离散的,可以大大缓解引入证据的问题
近似离散Mask
GNNExplainer
通过学习边和节点的软Mask来优化解释的预测,软Mask的值是初始化的,可学习的.
GNNExplainer组合这些Mask方案,通过元素乘法与原始图相结合
通过最大化原图预测和Mask后的预测之间的互信息优化Mask方案.
引入证据问题,缺乏全局视角
学习边和节点的soft mask。结合原始模型的参数,可以估计mask本身应当取得的值。缺陷是这种方法是对每一个输入的图有一个特定的解释,因而缺乏全局信息。
PGExplainer
学习近似的离散Mask来解释预测,训练了一个参数化的预测边Mask预测器
一个输入图,首先获得边的嵌入,然后预测器使用嵌入来计算这个边被选择的概率(重要性)
通过重新参数化技巧对近似的离散掩模进行采样。最后,Mask预测器通过最大化原来的预测和新的预测之间的相互信息来训练
是一种学习approximated discrete mask 的方法。通过训练是否有边的标签获得解释性。首先根据节点embedding获得边的embedding,之后进行边估计。由于所有边都使用同一个预测器,所以实际上是能够学习到全局信息的。
GraphMask
是一种事后解释的方法,每个GNN层中边的重要性
训练了一个分类器来预测边缘,可以在不影响原始预测的情况下删除
GraphMask 为每个 GNN 获得一个边掩码层,而 PGExplainer 只关注输入空间
采用post-hoc方法,与PGExplainer相似,预测边是否可被dropout。 GraphMask是对GNN中每一层对图结构进行边dropout操作。为了防止图结构被破坏,引入了一个可学习的连接参数。
ZORRO
使用不连续的Mask来识别重要的输入节点和节点特性,采用贪婪算法选择节点或节点特征
对于每个步骤,ZORRO 选择具有最高的逼真度分数的一个节点或者一个节点特征
使用discrete mask 方法。用贪心法计算每一个节点是否选择。而贪心算法也会带来局部最优问题。
Causal Screening
对于每一步,研究不同边的因果效应(ICE),并选择一条边加入到子图中.
学习边的因果关系。是否加边是构成一个新的子图的关键,因而这样就能分析每个边的影响。与ZORRO相似,采用的是贪心策略。
代理模型
假定输入示例的相邻区域中的关系不复杂,可以通过更简单的代理模型很好的捕获====>>>社交网络中可行吗?
对图形应用代理方法领域是具有挑战性的,因为图数据是离散的包含拓扑信息。
那么就不清楚如何定义输入图的相邻区域可解释的代理模型是合适的。
对一个给定的输入图的预测,他们首先获得一个局部的数据集,包含多个相邻数据对象和他们的预测,然后找一个适合可解释的模型学习这些数据集。
最后,来自可解释的模型被认为是对原始模型的输入图。
这些模型的区别在于:如何获取本地数据集和使用什么可解释的代理模型
GraphLime
扩展了LME算法,研究节点分类任务中不同节点的重要性,GraphLime考虑N跳邻居节点和它们的预
测作为它的本地数据集,n为GNN的层数
然后采用一种非线性代理模型对局部数据集进行拟合
GraphLime 只能提供节点特征的解释,而忽略了对图数据更重要的节点和边等图形结构,不能直接应用于图分类模型
一种Lime方法的扩展。这个方法考虑一个节点的N-hop的邻居节点,一般N取GNN的层数。之后使用Hilbert-Schmidt Independence Criterion (HSIC) Lasso 选择特征,得到的结果与原始GNN的结果做对比。这种方法由于只考虑了节点特征,因而对于边构成的结构信息有所忽视。
RelEx
通过结合代理模型的方法的思想建立模型和基于扰动的方法
给定目标节点和它的计算图(N-hop 邻居) ,它首先获得通过随机抽取连接的子图来建立一个局部数据集然后输入这些子图以获取他们的预测。
也是针对节点分类的一种解释性模型。对于数据集是随机选择N-hop的子图。与Lime方法不同的是这个方法在最后会使用Gumbel-Softmax的这种估计方法整理预测结果。因此结果的可信度会差一些。
PGM-Explainer
构建了一个概率图形模型为GNN提供实例级解释。利用随机节点特征获取局部数据集
给定一个输入图,每次PGM-Explainer 随机扰乱几个随机节点的计算图。然后对于计算图中的任何节点,PGM-Explainer记录一个随机变量,表明它的特征和它对 GNN 预测的影响多次重复这样的过程
一种基于概率图的instance-level的解释器。每次输入时,模型会随机扰动一些节点特征,观测这些特征如何影响最后结果。之后通过Grow-Shrink方法选择一些最显著的因变量(dependent variables),最后通过贝叶斯网络取解释。
分解方法
直接研究模型参数,分解项的总和等于原始的预测分数,将原始模型预测分数分解来衡量输入特征的重要性
建之分数分解规则以将预测分数分配到输⼊空间,以反向传播的⽅式逐层分布预测得分, 直到输⼊层为⽌

LRP
分解输出预测不同的节点重要性得分
对于目标神经元,它的得分表示为上一层神经元得分的线性近似
为了满足守恒性质,在事后解释阶段,邻接矩阵被视为 GNN 模型的一部分,因此在分数分配时可以忽略它; 否则,相邻矩阵也将接收分解后的分数
它只能研究不同节点的重要性,不能应用于图结构
主要分解最后预测得分来计算得分。这些分数直接反应了上一层隐藏层是输入了什么样的信息,所以就能找到贡献更多的神经元了。为了适应图这种数据,模型将图的邻接矩阵视作网络的一部分,这样它也能接受这种回馈信息了。由于这种模型能够反应神经元活性,所以理解似乎更容易。但是不同节点的重要性仍然未被分析。
Excitation BP
基于全概率公式的
它定义了当前层神经元的概率等于它输出到所有连接的总概率
与LRP相似,改进点在于定义了当前神经元在当前隐藏层拥有的概率与输出至下一层所有神经元的总概率。因此成了一个条件概率,解释性似乎更明了了。
GNN-LRP
学习了不同graph walk的重要性。将图上的传递过程用泰勒函数展开形式进行构建,而每一项就可以看成重要性
模型级
XGNN
XGNN 是一种通过图生成的方式去进行解释,这种生成的最后结果能够最大化的拟合目标的预测。XGNN是一种通过强化学习的方法做的,每一步预测这个边是否需要被纳入,然后将生成的图的结果与原始图的结果做对比,得到这个结构是否完备。同时XGNN考虑了规则信息,这些规则信息使得图有了约束,就如这篇文章本身讲的能够搞一些分子的化学意义了。
带有学习过程的解释方法倾向于更好的输入和预测之间的关系
数据集
解释必须是人类可理解的
数据,标签之间的关系可能GNN也不能捕获到
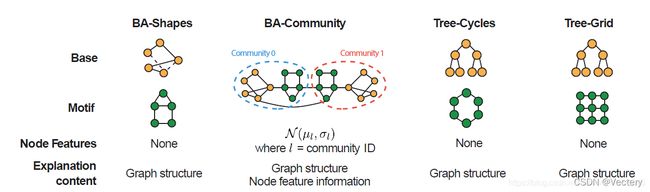
BA-shapes:
节点分类数据集,4个类别
对于每个图,它包含一个基本图(300个节点)和一个类似房子的motif
基图是由 Barabasi-Albert (BA)模型得到的,它可以生成具有优先连接机制的随机无标度网络在基图上添加随机边的同时,将母题附加到基图上。每个节点都根据它是属于基本图还是属于不同的主题空间位置进行标记。
BA-Community
一个具有8种不同标签的节点分类数据集
对于每个图,它是由两个随机添加边的 BA-shapes组合而得到的。节点标签由 BA-shapes的隶属关系及其结构位置确定。
Tree-Cycle:
它是一个具有2个不同标签的节点分类数据集。对于每个图,它由一个深度等于8的基本平衡树图和一个六节点循环图母图组成。这两个部分是随机连接的。基于图的节点的标签为0,否则为1。
Tree-Grids
它是一个具有两种不同标签的节点分类数据集。它与树循环数据集相同,只是树网格数据集使用了九个节点的网格模式,而不是循环模式。
BA-2Motifs
是一个具有两个不同图标的图分类数据集。通过在基本 BA 图上附加类房子图和五节点循环图等不同图形,得到800个图形。不同的图是基于类型的主题。
情感数据集
文本序列---->图
边:单词间的关系
点:单词
基于语义
不同词语的意思和情感标签,我们可以研究解释是否可以识别单词关键意义和不同单词之间的关系。
保真度
解释应该忠实于模型。他们应该识别对模型重要的输入特性
原始预测准确率 - 新预测的准确率
稀疏性
应该捕获最重要的输入特性忽略不相关的。
稳定性
准确性
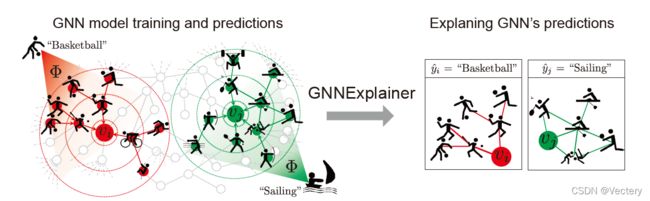
GNNExplainer: Generating Explanations for Graph Neural Networks
与模型无关,GNNExplainer会确定紧凑的子图结构和节点特征的一小部分,对GNN预测至关重要
Mask边和节点的特征
GNN预测和可能的子图结构的分布之间的互信息最大
可以为整个类的实例生成一致和简洁的解释。
其他方法并不能很好地整合关系信息,图的本质。因为这方面的成功是至关重要的机器学习的图形,任何解释 GNN 的预测应利用由图和节点特征提供的关系信息。
通过建立一个平均场变分近似和学习一个实数图掩码,选择 GNN 的重要子图,并用人工数据集解释精度
GNN只用了X和A,解释时也只考虑X和A
模型
对于节点 v v v, 其经过图神经网络后得到的embedding, 由其对应的邻居节点及特征决定, 分别计邻居组成的子图结构为 G c ( v ) G_{c}(v) Gc(v), 特征集合 为 X c ( v ) X_{c}(v) Xc(v),则节点的预测输出为
y ^ = Φ ( G c ( v ) , X c ( v ) ) \hat{y}=\Phi\left(G_{c}(v), X_{c}(v)\right) y^=Φ(Gc(v),Xc(v))
找出计算图和对模型 Φ \Phi Φ预测影响最大的节点特征子集
给定一个节点 v \mathrm{v} v, 我们的目标是识别出一个子图 G S ⊆ G c G_{S} \subseteq G_{c} GS⊆Gc和他们的特征 X S = X_{S}= XS= { x j ∣ v j ∈ G S } \left\{x_{j} \mid v_{j} \in G_{S}\right\} {xj∣vj∈GS} ,这些是对GNN预测 y ^ \hat{y} y^最为重要的.
最大化预测标签分布Y和解释之间的互信息 ===>>>最小化条件熵
max G S M I ( Y , ( G S , X S ) ) = H ( Y ) − H ( Y ∣ G = G S , X = X S ) \max _{G_{S}} M I\left(Y,\left(G_{S}, X_{S}\right)\right)=H(Y)-H\left(Y \mid G=G_{S}, X=X_{S}\right) maxGSMI(Y,(GS,XS))=H(Y)−H(Y∣G=GS,X=XS)
转化成
H ( Y ∣ G = G S , X = X S ) = − E Y ∣ G S , X S [ log P Φ ( Y ∣ G = G S , X = X S ) ] H\left(Y \mid G=G_{S}, X=X_{S}\right)=-\mathbb{E}_{Y \mid G_{S}, X_{S}}\left[\log P_{\Phi}\left(Y \mid G=G_{S}, X=X_{S}\right)\right] H(Y∣G=GS,X=XS)=−EY∣GS,XS[logPΦ(Y∣G=GS,X=XS)]
GNNEXPLAINER 的目标是通过获取与预测相互信息最高的Top Km个边。
显然, GNN是不满足凸函数假设的,但工作中发现基于上述目标函数,结合正则项, 对于所学的局部最优解已经有较好的解释能力。
对于期望 E G [ G S ] \mathbb{E}_{\mathcal{G}}\left[G_{S}\right] EG[GS], 通过一个掩码来实现, A c ⊙ σ ( M ) A_{c} \odot \sigma(M) Ac⊙σ(M), where M ∈ R n × n M \in \mathbb{R}^{n \times n} M∈Rn×n 。即,实际解释器要学习的, 即是掩码M.
进一步,一般我们希望了解“此样本为何被预测为某一个类别",而不是对全局模型的理解。故进一步修改目标函数为:
min M − ∑ c = 1 C 1 [ y = c ] log P Φ ( Y = y ∣ G = A c ⊙ σ ( M ) , X = X c ) \min _{M}-\sum_{c=1}^{C} 1[y=c] \log P_{\Phi}\left(Y=y \mid G=A_{c} \odot \sigma(M), X=X_{c}\right) minM−∑c=1C1[y=c]logPΦ(Y=y∣G=Ac⊙σ(M),X=Xc)
节点特征选择
同理, 也使用掩码实现。
X S F = { x j F ∣ v j ∈ G S } , x j F = [ x j , t 1 , … , x j , t k ] X_{S}^{F}=\left\{x_{j}^{F} \mid v_{j} \in G_{S}\right\}, \quad x_{j}^{F}=\left[x_{j, t_{1}}, \ldots, x_{j, t_{k}}\right] XSF={xjF∣vj∈GS},xjF=[xj,t1,…,xj,tk] for F t i = 1 F_{t_{i}}=1 Fti=1
综上,对于整个解释器,要优化的目标函数即是:
max G S , F M I ( Y , ( G S , F ) ) = H ( Y ) − H ( Y ∣ G = G S , X = X S F ) \max _{G_{S}, F} M I\left(Y,\left(G_{S}, F\right)\right)=H(Y)-H\left(Y \mid G=G_{S}, X=X_{S}^{F}\right) maxGS,FMI(Y,(GS,F))=H(Y)−H(Y∣G=GS,X=XSF)
此外, paper中提到使用reparametrization的trick来学习参数掩码。除却上述目标函数外,解释器还加入若干正则项限制,如element-wise entropy, 鼓励掩码离散惩晋过多非零项的掩码
数据集
人工合成数据集
Interpreting Graph Neural Networks for NLP With Differentiable Edge Masking
图数据的天然优势是为学习算法提供了丰富的结构化信息,节点之间邻接关系的设计成为了重要的先验信息和交互约束。然而,有一部分边上的消息是可以忽略的,论文首先提出方法在不影响模型预测效果的情况下,将图结构中冗余的边drop掉。通过分析剩余边上具有怎样的先验知识,实现对GNN的预测过程加以解释。
事后解释方法,识别不出必要的边
输入:训练完成的GNN
学习一个简单的分类器,可以针对每一层中的每个边,预测是否可以丢弃该边
GRAPHMASK 旨在通过可扩展的方式实现与擦除搜索相同的优点,从而满足上述的需求。也就是说,作者的方法对保留或丢弃边做出了可解释的硬性选择,从而使被丢弃的边与模型预测没有相关性,同时保持了易处理性。
GRAPHMASK 可以理解为子集擦除的一种可微的形式。其中,作者不是为每个给定的例子找到一个需要擦除的最佳子集,而是学习一个参数化的擦除函数,该函数可以预测是否应该保留第层的每条边 。
给定一个示例图 [外链图片转存失败,源站可能有防盗链机制,之外的任何边都不会影响模型的预测。由于作者的模型依赖于参数化的擦除函数,而不是对每条边单独进行选择,作者可以通过在训练数据集上摊开参数学习,这种策略避免了事后偏差。
旨在通过以可扩展的方式获得与删除搜索相同的有事来满足要求