推荐系统2--隐语义模型（LFM）和矩阵分解（MF）

一，背景

协同过滤（userCF，itemCF ）完全没有用到用户或者物品本身的属性，仅仅利用了用户与物品之间的交互信息就可以实现推荐。是一个可解释性很强，非常直观的模型，但是缺点在于：1，处理稀疏矩阵的能力比较弱，泛化能力弱。 为了解决这个问题，从协同过滤中衍生出矩阵分解模型（Matrix Factorization,MF）,并发展出矩阵分解的分支模型,比如隐语义模型和矩阵分解

隐语义模型和矩阵分解可以理解为类似的内容，都是在协同过滤共现矩阵的基础上，使用更稠密的隐形量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征，在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。

二，隐语义模型原理

假设每个用户都有自己的听歌偏好， 比如A喜欢带有小清新的， 吉他伴奏的， 王菲的歌曲，如果一首歌正好是王菲唱的， 并且是吉他伴奏的小清新， 那么就可以将这首歌推荐给这个用户。 也就是说是小清新， 吉他伴奏， 王菲这些元素连接起了用户和歌曲。 当然每个用户对不同的元素偏好不同， 每首歌包含的元素也不一样， 所以我们就希望找到下面的两个矩阵：
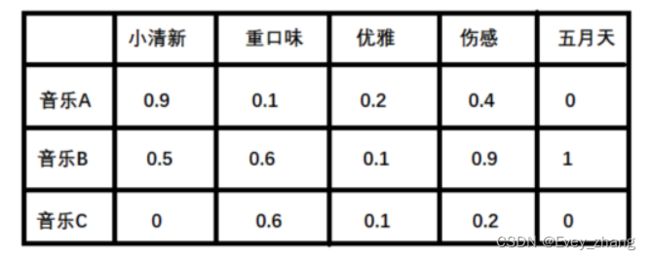
1，潜在因子----用户矩阵Q
这个矩阵表示不同用户对于不同元素的偏好程度，1代表很喜欢，0代表不喜欢。如下：

2，潜在因子----音乐矩阵P
表示每种音乐含有各种元素的成分，比如下表中， 音乐A是一个偏小清新的音乐， 含有小清新的Latent Factor的成分是0.9， 重口味的成分是0.1， 优雅成分0.2…

利用上面矩阵，得到张三对音乐A的喜欢程度：
张三对小清新的偏好 * 音乐A含有小清新的成分 + 张三对重口味的偏好 * 音乐A含有重口味的成分 + 张三对优雅的偏好 * 音乐A含有优雅的成分…,

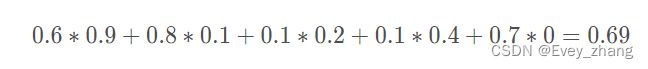
按照这个计算方式，每个用户对每首歌都可以得到相应的评分，最后得到评分矩阵：

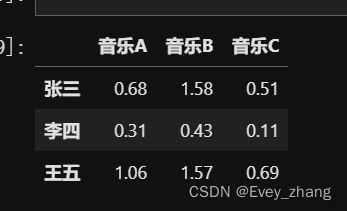
从上面的例子，隐含特征含义如下：
小清新，重口味，优雅，这些可以看做是隐含特征，通过这个隐含特征可以把用户的兴趣和音乐进行分类，其实就是找到了每个用户每个音乐的一个隐向量表达形式，这个隐向量可以反映出用户的兴趣和物品的风格，并能将相似的物品推荐给相似的用户。类似于把协同过滤算法进行了一种延伸，把用户的相似性和物品的相似性通过了一个叫做隐向量的方式进行表达。
但现实中，我们没有上面那两个矩阵，有的只是用户的评分矩阵，并且这个矩阵还非常稀疏（有些用户没有对某些物品进行评价）

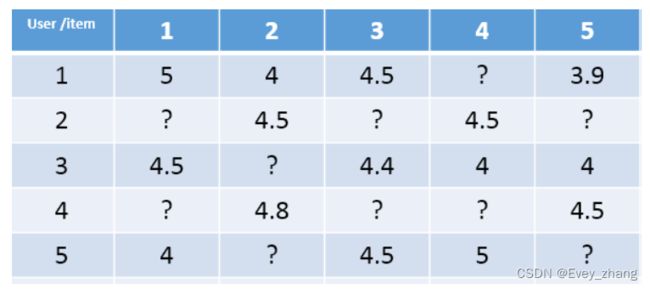
针对这个稀疏的矩阵，协同过滤算法想基于用户相似性或者物品相似性去填充这个矩阵不太容易，并且很容易出现长尾问题。所以，协同过滤的延伸：矩阵分解，或者叫隐语义模型渐渐得到了发展

隐语义模型/矩阵分解 的原理：想办法基于最后的评分矩阵，去找到上面例子中的那两个矩阵，也就是用户兴趣和物品的隐向量表达，然后就把这个评分矩阵分解成Q和P两个矩阵乘积的形式，这时就可以基于这两个矩阵去预测某个用户对某个物品的评分了。然后基于这个评分去进行推荐。

三，矩阵分解算法原理

现实中我们得到的是残缺的评分矩阵，通过矩阵分解算法，可以通过分解评分矩阵，得到用户和物品的隐向量，也就是上面的用户矩阵Q和物品矩阵P，下图给出矩阵分解的过程：

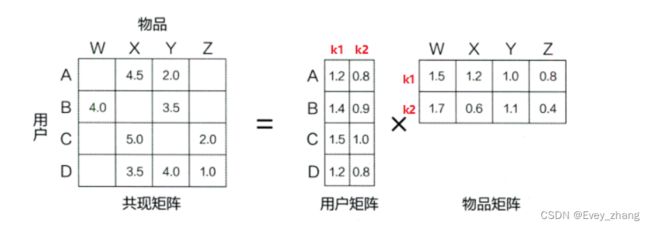
矩阵分解算法将MN维的共享矩阵R分解成mk维的用户矩阵U和k*n维的物品矩阵V相乘的形式。其中m是用户数量，n是物品数量，k是隐向量维度，也就是隐含特征个数，只不过这里的隐含特征变得不可解释了，也就是我们不知道具体含义了，要模型自己去学。K的大小决定了隐向量表达能力的强弱，k越大，表达信息就越强，理解起来就是把用户的兴趣和物品的分类划分的越具体了。
有了用户矩阵和物品矩阵，则计算用户u 对物品i 的评分，只需要：

这里的Pu 是用户u 的隐向量，就类似上面的张三向量，并且是一个列向量。qi是物品i的隐向量，就类似上面的音乐A向量，也是一个列向量。所以才用Pu的转置与qi相乘，得到用户的最终评分。pu,k和qk,i 是模型的参数，也是我们需要计算的。pu,k度量的是用户u的兴趣与第k个隐类的关系，qk,i 度量的是第k个隐类与物品i之间的关系。下面来求两个矩阵里面的具体参数。

四，矩阵分解算法的求解

矩阵分解，最常见的方法是特征值分解（EVD）或者奇异值分解（SVD）。但这两种方法不适合直接使用。首先是EVD,它要求分解的矩阵是方阵，显然用户-物品矩阵不满足这个要求，而传统的SVD分解，会要求原始矩阵是稠密的，我们这里得到的用户物品评分矩阵一般情况下是非常稀疏的，如果想用奇异值分解，必须对缺失元素进行填充，而一旦补全，空间复杂度会非常高，而且补的不一定对，并且SVD分解计算复杂度非常高，我们的用户-物品矩阵非常大，所以基本上无法使用。

4.1 Basic SVD

2006年的Netflix Prize之后，Simon Funk 公布了一个矩阵分解算法叫做Funk-SVD，后来被Netflix Prize的冠军Koren称为 Latent Factor Model(LFM)。**Funk-SVD 的思想很简单：把求解上面两个矩阵的参数问题转换成一个最优化问题，可以通过训练集里面的观察值利用最小化来学习用户矩阵和物品矩阵。**具体理解如下：
有了用户矩阵和物品矩阵的话，我们如果想要计算用户u 对物品i的评分，只需要

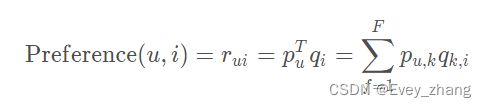
现在，我们有真实的rui，但是没有pu和qi。那么我们可以初始化一个，随机初始化一个用户矩阵U 和一个物品矩阵V,这样就有pu 和qi了。当然，随机初始化的肯定不准，但是有了pu 和qi之后，就可以计算一个猜测的rui，即：

这时候，猜测和真实值之间会有一个误差：

有了误差，就可以计算出总的误差平方和：

有了误差（也就是损失），我们就可以想办法进行训练，将SSE降到最小，这样我们的两个矩阵参数就计算出来了（这就是训练深度学习模型时候常用的套路），于是就把求解用户矩阵和物品矩阵的问题，转换成了最优化的问题，目标函数是：

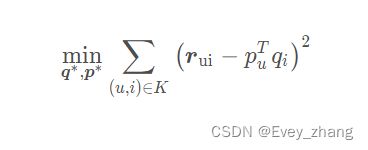
这里的K 表示所有用户评分样本的集合。
我们拿到一个用户物品评分矩阵，要去计算两个参数矩阵U和V,可以利用求解神经网络模型参数的思路来计算这两个矩阵：
1.首先先初始化这两个矩阵
2.把用户物品评分矩阵里面那些已经评过分的样本当做训练集的label,把对应的用户和物品的隐向量当做features,这样就会得到（features,label），相当于是训练集
3.通过两个隐向量乘积得到预测值pred
4.根据label 和pred 计算损失
5.反向传播，通过梯度下降的方式，更新两个隐向量的值
6.未评过分的那些样本当做测试集，通过两个隐向量就可以得到测试集的label值
7.这样就填完了矩阵，下一步就可以进行推荐了

得到了目标函数，接下来使用梯度下降算法来降低损失。我们需要对目标函数求偏导，得到梯度。我们的目标函数如果是上面的SSE,下面来推导一下最后的导数：

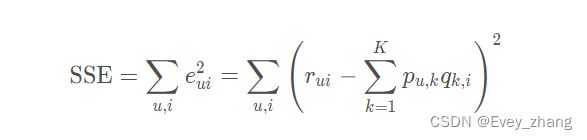
为了让公式更简单，将SSE公式中前面的2约掉，即可以令SSE等于：

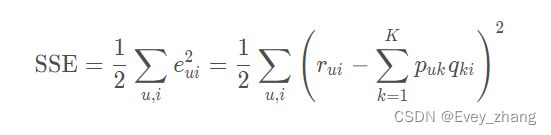
这样，梯度前面就没有系数2了，有了梯度，接下来就可以用梯度下降算法来更新梯度了：

这里的yita 是学习率，用来控制步长。得到了更新的式子，下面讨论更新如何进行。有两种选择：
1，计算完所有已知评分的预测误差（即所有的训练数据）后再对P,Q进行更新。
2，每计算完一个eui后（也就是一个训练数据的预测误差）立即对pu 和 qi 进行更新。
第一种叫做批梯度下降，第二种叫做随机梯度下降。二者的区别在于，批梯度下降在下一轮迭代才能使用本次迭代的更新值，随机梯度下降本次迭代中当前样本使用的值可能就是上一个样本更新的值。由于随机性可以带来很多好处，比如有利于避免局部最优解，所以现在大多倾向于使用随机梯度下降进行更新。这就是运用梯度下降的矩阵分解算法了。称之为Basic SVD.

Basic SVD 算法存在的问题是：当两个矩阵很大的时候，往往容易陷入过拟合的困境，这时，就需要在目标函数SSE 上面加上正则化的损失，就变成了RSVD。

4.2 RSVD

在目标函数中加入正则化参数（加入惩罚项），对于目标函数来说，Q矩阵和V矩阵中的所有值都是变量，这些变量在不知道哪个变量会带来过拟合的情况下，对所有的变量都进行惩罚：

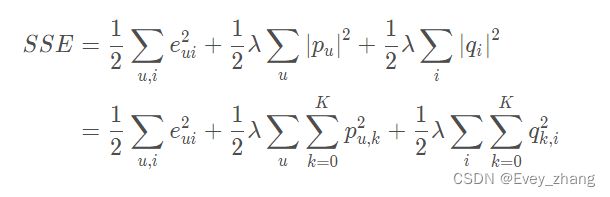
此时目标函数对参数的导数与basic SVD 相比较，前面那部分没变，加入了后面的梯度，具体表示形式如下：

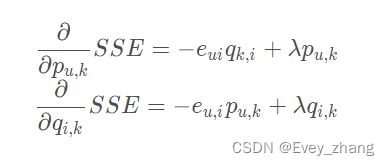
这样正则化之后，梯度的更新公式如下：

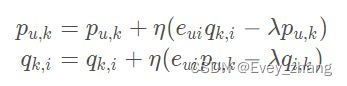
4.3 消除用户和物品打分的偏差

通过上面隐向量的方式，就可以将用户和物品联系到了一起，但实际情况中，单纯的

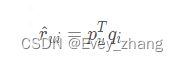
是不够的。还要考虑一些其他的因素，比如一个评分系统，有些固有的属性和用户以及物品都无关，而用户有些属性与物品无关，物品有些属性与用户无关。因此，Netfix Prize 中提出了另一种LFM,在原来的基础上增加偏置项，来消除用户和物品打分的偏差。预测公式如下：

这个预测公式加入三个偏置项：
\mu ：训练集中所有记录的评分的全局平均数。在不同网站中，整体评分分布会存在差异。比如有的网站中用户喜欢打高分，有的网站中用户喜欢打低分。全局平均数可以标识网站本身对用户评分的影响
b_{u} ：用户偏差系数，可以使用用户u给出的所有评分的均值，也可以当做训练参数（个人理解是最开始随机初始化一个值，然后随着训练过程来优化这个参数)。这一项表示用户评分习惯中与物品没有关系的因素。比如有些用户比较苛刻，对物品要求高，因此他对所有物品的打分都会偏低一些。有些用户对物品的打分普遍偏高。
b_{i} : 物品偏差系数，可以使用物品i 收到的所有评分的均值，也可以当做训练参数。这一项表示了物品接受的评分中和用户没有关系的因素。比如有些物品（由于本身质量高或者社会文化因素的影响）本身质量就很高，因此获得的评分相对就比较高。有些物品本身质量很差，因此获得的评分相对比较低。

加入b_{u},b_{i}之后，矩阵分解得到的隐向量更能反映不同用户对不同物品的“真实”态度差异，也更容易捕捉到评价数据中有价值的信息，从而避免推荐结果有偏。此时SSE变成了：

如果把b_{u}和b_{i}当做训练参数的话，那么他俩的梯度是（此处可以复习一下复合函数求导链式法则）：

更新公式：

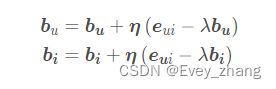
4.4 SVD++

前面的LFM模型没有显示的考虑用户的历史行为对用户评分预测的影响。但是可以知道的是，用户的历史行为记录，对当下物品的预测也可以作为一个参考。所以Netfix Prize 中提出了一个模型叫做SVD++,它将用户历史评分的物品加到了LFM模型里。也就是说，上面的那些矩阵分解，是只分解当前的共现矩阵，比如某个用户u 对某个物品i 的评分，就单纯的分解成用户u 的隐向量与物品i的隐向量乘积再加上偏置项。这时候注意并没有考虑该用户评分的历史物品，所以SVD++ 把这个考虑了进去。下面介绍SVD++的演变过程。
首先把itemCF的预测算法改成一个可以学习的模型，就像LFM那样，ItemCF的预测算法公式如下：

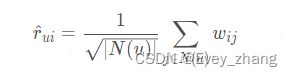
这个式子是预测用户u 对于物品i 的打分，其中N(u)表示用户u 打过分的历史物品，Wij 表示物品i，j的相似度。这里的相似度不再是ItemCF那样，通过向量计算的，而是像LFM那样，让模型自己学出这个参数来，那么相应的就可以通过优化的思想：

这个模型存在一个问题，就是w比较稠密，存储需要很大的空间，因为如果有n个物品，那么模型的参数就是n^{2},参数一多，就容易造成过拟合。所以Koren提出应该对w矩阵进行分解，将参数降到了2nF：

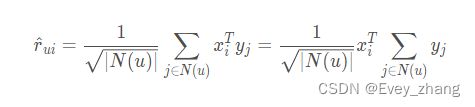
相当于用x_{i}^{T}y_{j}来代替wij，这里xi,yj 是两个F维的向量。xi 代表当前物品，yj代表历史物品。这里其实就是又对物品i和某个用户u买过的历史物品学习一波隐向量，这次是F维，为了衡量出物品i和历史物品j之间的相似相来。这时，参数的数量降了下来，并同时也考虑进来了用户的历史物品记录。所以这个和之前的LFM相加就得到了：

前面是我们之前分析的LFM模型，后面的这个是考虑进了用户购买的历史物品。但是这样感觉参数太多了，所以Koren提出了，令xi = qi，因为既然同是商品i,就没有必要学习两个隐向量了，所以得到了该模型的最终预测方式：

这一个就是SVD++模型了。有了预测函数，然后也知道真实值，就可以由损失函数对各个参数求偏导，和上面一样，下面直接给出导数：

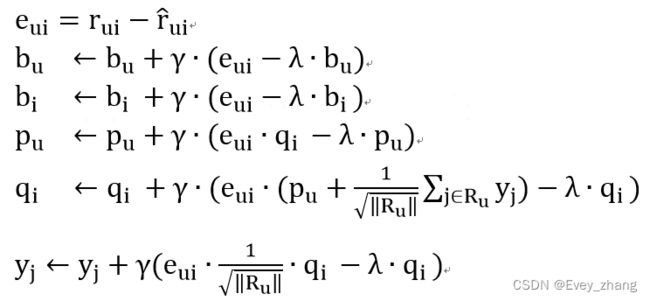
5，编程实现

用代码来实现上面的算法，已知的评分矩阵如下：

任务是根据上面的评分矩阵，预测Alice 对物品5的评分。
首先回顾一下ItemCF和UserCF对于这个问题的解决思路。
（1）ItemCF：根据已有的用户打分计算物品之间的相似度，得到物品的相似度矩阵，根据这个矩阵，选出前K 个与物品5最相似的物品，然后基于Alice 对这K个物品的打分，预测Alice 对物品5的打分（有一个加权公式）。然而现实中，两个矩阵非常稀疏的话，Alice同时对两个相似物品打分的概率可能会比较小。
（2）UserCF：根据已有的用户打分计算用户之间的相似度，得到用户的相似度矩阵，根据这个矩阵，选出与Alice最相似的K个用户，然后基于这K个用户对物品5的打分，预测Alice 对物品5的打分（有一个加权公式）。同样，现实中，两个矩阵非常稀疏的话，两个相似用户同时对物品5打分的概率可能会比较小。
而且这两种方法，没有考虑到全局的物品或用户，只是基于了最相似的例子，很可能是有偏的。
SVD解决这个问题的做法如下：
1）初始化用户矩阵P 和物品矩阵Q:P的维度是[users_num,F],Q的维度是[items_num,F]。F 是隐向量的维度。也就是通过隐向量的方式把每个用户，用F维的特点表示出来（只不过这F维具体是什么含义，无法直观表示出来）。同样，把每个物品，也用F维的特点表示出来。初始化这两个矩阵的方法很多，根据经验，随机数需要跟1/sqrt(F)成正比。
2）有了这两个矩阵，可以根据用户已经打分的数据来更新参数。基本思想是：遍历用户，对于每一个用户，遍历它打分的物品，这样拿到了该用户和物品的隐向量。对于特定用户对特定物品的评分，就是两者的隐向量相乘再加上偏置。这时候与真实评分有个差距，根据上面的随机梯度下降方法就可以进行参数更新。
可以边对照下面的公式边理解代码：



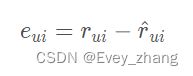
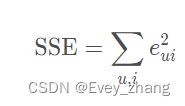
梯度更新公式如下：

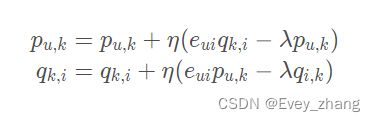
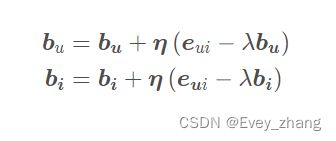
import pandas as pd
import numpy as np
import random
import math

class BasicSVD():
    def __init__(self, rating_data, F=5, alpha=0.1, lmbda=0.1, max_iter=100):
        self.F = F           # 这个表示隐向量的维度
        self.P = dict()          #  用户矩阵P  大小是[users_num, F]
        self.Q = dict()     # 物品矩阵Q  大小是[item_nums, F]
        self.bu = dict()   # 用户偏差系数
        self.bi = dict()    # 物品偏差系数
        self.mu = 1.0        # 全局偏差系数
        self.alpha = alpha   # 学习率
        self.lmbda = lmbda    # 正则项系数
        self.max_iter = max_iter    # 最大迭代次数
        self.rating_data = rating_data # 评分矩阵
        
        # 初始化矩阵P和Q, 方法很多， 一般用随机数填充， 但随机数大小有讲究， 根据经验， 随机数需要和1/sqrt(F)成正比
        cnt = 0    # 统计总的打分数， 初始化mu用
        for user, items in self.rating_data.items():
            self.P[user] = [random.random() / math.sqrt(self.F)  for x in range(0, F)]
            self.bu[user] = 0
            cnt += len(items) 
            for item, rating in items.items():
                if item not in self.Q:
                    self.Q[item] = [random.random() / math.sqrt(self.F) for x in range(0, F)]
                    self.bi[item] = 0
        self.mu /= cnt
        
    # 有了矩阵之后， 就可以进行训练, 这里使用随机梯度下降的方式训练参数P和Q
    def train(self):
        for step in range(self.max_iter):
            for user, items in self.rating_data.items():
                for item, rui in items.items():
                    rhat_ui = self.predict(user, item)   # 得到预测评分
                    # 计算误差
                    e_ui = rui - rhat_ui
                    
                    self.bu[user] += self.alpha * (e_ui - self.lmbda * self.bu[user])
                    self.bi[item] += self.alpha * (e_ui - self.lmbda * self.bi[item])
                    # 随机梯度下降更新梯度
                    for k in range(0, self.F):
                        self.P[user][k] += self.alpha * (e_ui*self.Q[item][k] - self.lmbda * self.P[user][k])
                        self.Q[item][k] += self.alpha * (e_ui*self.P[user][k] - self.lmbda * self.Q[item][k])
                    
            self.alpha *= 0.1    # 每次迭代步长要逐步缩小
    
    # 预测user对item的评分， 这里没有使用向量的形式
    def predict(self, user, item):
        return sum(self.P[user][f] * self.Q[item][f] for f in range(0, self.F)) + self.bu[user] + self.bi[item] + self.mu   

# 定义数据集， 也就是那个表格， 注意这里我们采用字典存放数据， 因为实际情况中数据是非常稀疏的， 很少有情况是现在这样
# user： 1,2,3,4,5
# item：A,B,C,D,E

def loadData():
    rating_data={1: {'A': 5, 'B': 3, 'C': 4, 'D': 4},
           2: {'A': 3, 'B': 1, 'C': 2, 'D': 3, 'E': 3},
           3: {'A': 4, 'B': 3, 'C': 4, 'D': 3, 'E': 5},
           4: {'A': 3, 'B': 3, 'C': 1, 'D': 5, 'E': 4},
           5: {'A': 1, 'B': 5, 'C': 5, 'D': 2, 'E': 1}
          }
    return rating_data
 
# 接下来就是训练和预测
rating_data = loadData()
basicsvd = BasicSVD(rating_data, F=10)
basicsvd.train()
for item in ['E']:
    print(item, basicsvd.predict(1, item))
 

6，总结

本文首先整理了一下隐向量的含义，通过举例方式看了一下用户矩阵和物品矩阵的隐特征，评分矩阵如何分解成两个矩阵。
然后整理隐语义模型：基于现有的评分矩阵分解成用户矩阵和物品矩阵相乘的方式，然后学习后面两个矩阵的数字表示。
隐语义模型可以理解成是与矩阵分解同样的内容。传统SVD计算复杂度太高，因此这里把求解隐向量的问题转成最优化问题进行求解。介绍了SVD,RSVD，SVD++等集中常用的训练求解隐向量的算法。
矩阵分解为什么比协同过滤有更强的泛化能力？
矩阵分解算法中，由于隐向量的存在，使得任意的用户和物品之间都可以得到预测分值，求解隐向量的过程其实是对评分矩阵进行全局拟合的过程，这个过程考虑了所有的用户和评分，因此隐向量是利用全局信息生成的，具有更强的泛化能力。
协同过滤算法，只是基于相似的局部个体，而且，itemCF中，即使找到了与目标物品j相似的另外K个物品，同一个用户同时给这K个物品打分的概率也比较低。userCF中，即使找到了与用户i 相似的另外K个用户，这K个用户同时对物品j打过分的概率也比较低。因此无法得到全局信息。
矩阵分解算法的优缺点：
优点：

• 泛化能力强：一定程度上解决了稀疏问题
• 空间复杂度低：由于用户和物品都用隐向量的形式存放，少了用户相似度矩阵和物品相似度矩阵，空间复杂度由n^{2}下降到了（n+m)*f
• 更好的扩展性和灵活性：矩阵分解的最终产物是用户和物品隐向量，这与深度学习的embeding不谋而合。因此矩阵分解的结果非常便于与其他特征进行组合和拼接，并可以与深度学习无缝结合。

缺点：

• 矩阵分解算法只用到了评分矩阵，没有考虑用户特征，物品特征和上下文特征，这使得矩阵分解丧失了利用很多有效信息的机会，同时在缺乏用户历史行为时，无法进行有效推荐。为了解决这个问题，逻辑回归模型以及后续的因子分解机模型，凭借其天然的融合不同特征的能力，逐渐在推荐系统领域得到了更广泛的应用。

参考：

• 王喆-《深度学习推荐系统》
• AI上推荐 之 隐语义模型(LFM)和矩阵分解(MF)