基于pytorch神经网络的学习（二）

在上一节中，我们构建一个简单的全连接网络模型实现手写字体识别的任务，由于Mnist数据集的数据是图片，使用全连接网络显然不合适。全连接中输入为（batch_size，784），但是对于卷积神经网络处理图像数据而言，输入要求为（batch_size，颜色通道数，28，28）的格式。在全连接网络中，每个像素点都是相互独立的。而卷积神经网络是根据一个卷积核计算特征，综合考虑内部像素点的特征，表明像素点间是有关联的。因此本节采样卷积神经网络来进行识别分类任务。

本节使用的torchvision包中有内置数据集模块datasets下载，预处理模块transforms（比如将数据转为tensor格式）。

import torch
import numpy as np
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
import numpy as np

构建训练集和验证集 

#训练集
train_dataset = datasets.MNIST(root='./data',
                              train=True,
                               transform=transforms.ToTensor(),      #转为Tensor格式
                               download=True)
#验证集
test_dataset = datasets.MNIST(root='./data',
                              train=False,
                               transform=transforms.ToTensor())

 下载完成

 网络模型的构建 。

class CNN(nn.Model):
    def __init__(self):
        super(CNN,self).__init__()
        self.conv1=nn.Sequential(
        nn.Vonv2d(
            in_channels=1,        #输入为（1，28，28）
            out_channels=16,       #输出特征图的个数为16（卷积核的个数）
            kernel_size=5,          #卷积核的大小（5，5）
            stride=1,               #卷积核的步长
            padding=2,               #边界填充。如果希望卷积后的大小和输入一样，需要设置padding=(kernel_size-1)/2
    ),                            #得到输出为（16，28，28）
        nn.ReLU(),                         #特征提取后需要进行非线性映射
        nn.MaxPool2d(kernel_size=2)        #进行池化操作，输出结果为（16，14，14）
    )
        self.conv2 = nn.Sequential(                 #经过池化后变为（16，14，14）作为输入
        nn.Conv2d(16,32,5,1,2),                  #输出为（32，14，14）
        nn.ReLU(),
        nn.Conv2d(32,32,5,1,2),                #输出为（32，14，14）
        nn.ReLU(),
        nn.MaxPool2d(2)                         #输出为（32，7，7）
    )
        self.conv3=nn.Sequential(
        nn.Conv2d(32,64,5,1,2),                  #输出为（64，7，7）
        nn.ReLU()
    ) 
        self.out = nn.Linear(64*7*7,10)             #经过全连接层
    
     def forward(self,x):
        x=self.conv1(x)
        x=self.conv2(x)
        x=self.conv3(x)
        x=x.view(x.size(0),-1)                   #flatten操作，得到二维的矩阵（batch_size,64*7*7）
        output=self.out(x) 
        return output

在pytorch中规定channel_first也就是颜色通道写在第一个位置。in__channel根据上一层的输出决定，而out_channel需要自己设置输出多少个特征图。kernel_size表示卷积核的大小，卷积核越小，得到的特征特就越多。stride表示卷积核的步长，卷积核是一个滑动的窗口，表示一次平移多少个单元。由于卷积过程中对边界的信息提取的较少，为了更好的提取边界的特征，通过padding来加上数值0填充边界的信息，padding=1表示加上一圈的0。MaxPool2d池化进行一个压缩，一般来说将尺寸压缩一半。

self.conv1=nn.Sequential(
        nn.Conv2d(
            in_channels=1,        #输入为（1，28，28）
            out_channels=16,       #输出特征图的个数为16（卷积核的个数）
            kernel_size=5,          #卷积核的大小（5，5）
            stride=1,               #卷积核的步长
            padding=2,               #边界填充。如果希望卷积后的大小和输入一样，需要设padding=
        ),

我们看看经过self.conv1中的nn.Conv2d的输出为多少？首先输入为（1，28，28），经过卷积后out_channel为16，所以输出为（16，h，w ）。然而h和w计算公式为：

[h(w)-kernel_size+2*padding]/stride+1。根据计算得到，h=28,w=28。最终输出为（16，28，28）。因此如果需要保证输入和输出大小不变，要设置padding的值，常见的组合为keinel_size=5,padding=2或者keinel_size=3,padding=1。

self.out = nn.Linear(64*7*7,10)

最终得到（64，7，7）的特征图并不是一个特征不能直接作为最终分类结果，由于分类任务的输出结果为10个类别的概率值，因此需要将特征图转化为一个特征，即转化为一个特征向量。其中特征总数为64*7*7。所以定义一个全连接层输入为64*7*7，输出为10。

     def forward(self,x):
        x=self.conv1(x)
        x=self.conv2(x)
        x=self.conv3(x)
        x=x.view(x.size(0),-1)      #flatten操作，得到二维的矩阵（batch_size,64*7*7）
        return output
    

x.view与x.reshape操作一样，得到二维的矩阵。由于x是四维向量为（batch_size, out_channel, h, w），其中x.size[0]表示batch_size的维度不变；-1表示自动计算（比如一个矩阵[5,4]经过[2,-1]得到[2,10]）所以最后得到的数值等于out_channel×h×w=64×7×7。一个特征图不能直接进行全连接操作，必需进行特征转化，接下来才能进入全连接层计算。

准确率作为模型的评估指标

def accuracy(predictions,labels):
    pred = torch.max(prediction.data,1)[1]
    rights = pred.eq(labels.data.view_as(pred)).sum()
    return rights, len(labels)

开始训练网络模型。

net = CNN()

#损失函数
criterion = nn.CrossEntropyLoss()

#优化器
optimizer = optim.Adam(net.parameters(), lr=0.001)  #网络中所有参数都要更新

#开始训练循环
for epoch in range(num_epochs):
    
    #当前的epoch结果保存下来
    train_rights = []
    
    for batch_idx, (data, target) in enumerate(train_loader):
        net.train()
        output = net(data)
        loss = criterion(output,target)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        right = accuracy(output, target)
        train_rights.append(right)
        
        if batch_idx % 100 ==0:
            net.eval()
            val_rights = []
            
            for (data, target) in test_loader:
                output = net(data)
                right = accuracy(output, target)
                val_rights.append(right)
                
            #准确率的计算
            train_r = (sum([tup[0] for tup in train_rights]), sum([tup[1] for tup in train_rights]))
            val_r = (sum([tup[0] for tup in val_rights]), sum([tup[1] for tup in val_rights]))
            
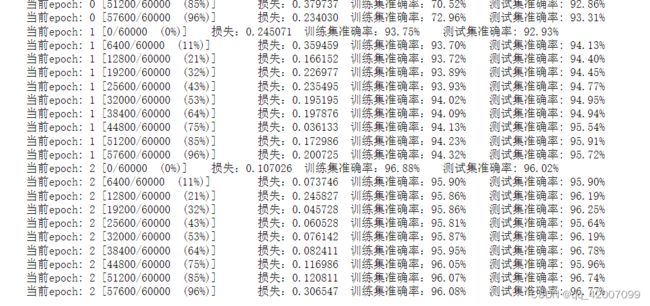
            print('当前epoch: {} [{}/{}  ({:.0f}%)]\t损失：{:.6f}\t训练集准确率：{:.2f}%\t测试集准确率: {:.2f}%'.format(
                  epoch, batch_idx * batch_size, len(train_loader.dataset),
                  100. *batch_idx / len(train_loader),
                  loss.data,
                  100. * train_r[0].numpy() / train_r[1],
                  100. * val_r[0].numpy() / val_r[1]))
        

可以看到相较于前一节的全连接网络，使用卷积神经网络的准确率提高了。