人工智能大作业----八数码问题
人工智能大作业----八数码问题
原文指路
(版权声明:本文为CSDN博主「Lwhere~」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/Lwhere_/article/details/103068116)
原文文章已经写的很全了,但是可能有些地方不适用于VS新的版本,我做了些许修改,以下代码适用于VS2015。
做实验的各位希望能进原文好好看看再来粘代码。不然根本不知道是怎么做的。
修改处:(1)在run()函数里判断哪个节点更优的时候,将判断值F改为了g,因为相同节点的H(评估函数值)肯定是一样的;
(2)给run()函数加了一个参数H,表示使用的评估算法,这个H在main主函数里修改。(或者你也可以改为H需要用户输入。)
(3)读取节点依然使用freopen重定向,但之后为了运行的时候黑窗不闪退,又重定向了回来。
(4)我建立的是win32工作区,当时没有选择空项目,所以自动带了“stadfx.h”“targetver.h”,这两个头文件我不会放在下面,因为没做修改;创建的是空项目的同学把每个文件里的#include"stadfx.h"删了就行,不然会出错!
(5)给每个头文件加了防重定义的宏指令。
(6)把原文的board变量改名为了arc变量。
(7)改变了一下黑窗颜色。
代码:
1.function.h
#pragma once
#ifndef _FUNCTION_H_
#define _FUNCTION_H_
#include"global.h"
#include"stdafx.h"
bool success(const int &e, const int&s); //检查是否到达目标路径
bool checkvalid(const int& cur, const int& tar); //检查是否有解
int H1(int curState, int tarState); //启发函数1
int H2(int curState, int tarState); //启发函数2
int H3(int curState); //启发函数3
int H4(int curState, int tarState); //启发函数4
int F(const Snode &e); //返回状态的F值
int arc_toState(const arc &se); //二维数组转换为一维数字
void state_toArc(int e, arc se); //一维数字转换为二维数组
void inPut(arc s); //输入初始序列和目标序列
void outPut(arc tmp); //输出状态的state值的矩阵形式
void findPath(int pre, int size, int step); //找到最优解的路径
int run(const int&st, const int &ed,int H); //运行A*函数算法主体
void goPath(int step); //当算法运行完毕,检查
#endif // !_FUNCTION_H_
2.global.h
#pragma once
#ifndef _GLOBAL_H_
#define _GLOBAL_H_
#include"stdafx.h"
#include3.function.cpp
#include"stdafx.h"
#include"function.h"
//一维数字转换为二维数组
void state_toArc(int e, arc se)
{
for (int i = 3; i >= 1; i--)
for (int j = 3; j >= 1; j--)
{
se[i][j] = e % 10;
e /= 10;
}
}
//将二维数组转换为一维数字
int arc_toState(const arc &se) {//注意e 一定要加上&,不然不能改变e的值
int e = 0;
for (int i = 1; i <= 3; ++i)
for (int j = 1; j <= 3; ++j)
e = e * 10 + se[i][j];
return e;
}
//返回Snode的F值
int F(const Snode &e) {
return e.g + e.h;
}
bool success(const int& cur, const int &tar) {
return(H1(cur, tar) == 0);
}
//检查是否可达
bool checkvalid(const int& cur, const int& tar) {
int cur_n = 0, tar_n = 0;
arc curr, tarr;
state_toArc(cur, curr);
state_toArc(tar, tarr);
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < i; j++)//找第i+1个元素后面所有的非0元素,如果元素比它小,那就对应逆序数+1
{
if ((curr[i / 3 + 1][i % 3 + 1] != 0) && (curr[j / 3 + 1][j % 3 + 1] != 0) && (curr[i / 3 + 1][i % 3 + 1] < curr[j / 3 + 1][j % 3 + 1])) cur_n++;
if ((tarr[i / 3 + 1][i % 3 + 1] != 0) && (tarr[j / 3 + 1][j % 3 + 1] != 0) && (tarr[i / 3 + 1][i % 3 + 1] < tarr[j / 3 + 1][j % 3 + 1])) tar_n++;
}
}
return (cur_n & 1) == (tar_n & 1);
}
//启发函数1
int H1(int curState, int tarState)
{
//找当前状态与目标状态的位置不同的非0数字个数
int num = 0;
for (int i = 0; i < 9; i++) {
if ((curState % 10 != tarState % 10)) ++num;
curState /= 10;
tarState /= 10;
}
return num;
}
//启发函数2
int H2(int curState, int tarState) {
//找当前状态要移动到目标的最短路径,返回所有状态的最短路径之和
int num = 0;
//引入一种新的数组,这个数组的下标值代表的是元素(即key值代表的是value),value值代表的是位置值。
int cu[9], ta[9];
int cur = curState, tar = tarState;
for (int i = 8; i >= 0; i--) {
cu[cur % 10] = ta[tar % 10] = i;
cur /= 10;
tar /= 10;
}
//含义是,数字1-8的状态序列到目的序列,它们不同的位置值之差,cu[i] i代表是哪个位置,值代表的是它的位置值0-8。
//位置值之间的移动的最小步骤不是简单相减,而是要根据它在矩阵上的结构特点,比如位置值0和3,实际上移动过去只需要一步
//位置值0-8在3*3矩阵上具体的位置移动值应该是 |xc-xt|+|yc-yt|
for (int i = 1; i <= 8; i++) {
num += abs(cu[i] / 3 - ta[i] / 3) + abs(cu[i] % 3 - ta[i] % 3);
}
return num;
}
//启发函数3
int H3(int curState)
{ //返回逆序数目*3
int num = 0;
arc curr;
state_toArc(curState, curr);
for (int i = 0; i < 9; i++) {
for (int j = i + 1; j < 9; j++)
{
if ((curr[i / 3 + 1][i % 3 + 1] != 0) && (curr[j / 3 + 1][j % 3 + 1] != 0) && (curr[i / 3 + 1][i % 3 + 1] > curr[j / 3 + 1][j % 3 + 1]))
++num;
}
}
return num * 3;
}
//启发函数4
int H4(int curState, int tarState) {
//综合H1与H3
return (H1(curState, tarState) + H3(curState));
}
void inPut(arc s) {
for (int i = 1; i <= 3; i++) {
for (int j = 1; j <= 3; j++) {
cin >> s[i][j];
}
}
}
void outPut(arc tmp) {
for (int i = 1; i <= 3; ++i) {
for (int j = 1; j <= 3; ++j)
cout << tmp[i][j] << " ";
puts("");
}
}
//运行open算法,返回值取最短路径的step值
int run(const int&st, const int &ed , int H) {
if (!checkvalid(st, ed)) return -1;//检测是否可达
//清理上一次程序运行时产生的数据。
open_key.clear();
open_value.clear();
closed.clear();
path.clear();
/*将初始结点放入open表中*/
int index = 0; //递增的序号值,唯一标识
/*此处H2可修改为H1\2\3\4*/
switch (H) {
case 1:H = H1(st, ed); break;
case 2:H = H2(st, ed); break;
case 3:H = H3(st); break;
case 4:H = H4(st, ed); break;
}
//cout << "该节点的H为:"<
Snode start(st, 0, H, index++, -1); //初始化初始结点start的值,其前驱路径的标号是-1,代表不存在
open_key.insert(make_pair(H, start)); //将初始结点放入open_key表中
open_value.insert(make_pair(start, H));//将初始结点放入open_value表中
//cout<< (open_key.begin()->second).state;
/*对后续结点进行启发式搜索*/
while (open_key.size())
{
Snode mixNode = open_key.begin()->second; //取出open的第一个元素(该元素也是f值最小的结点)进行扩展
open_key.erase(open_key.begin()); //从open表中清除
open_value.erase(open_value.lower_bound(mixNode));
closed.insert(make_pair(mixNode.state, true)); //将序列放入closed表中
path.push_back(mixNode); //将结点的具体结构放入path中,push_back()放在队尾
/*如果是已经到达目标路径,返回最短路径值step*/
if (success(mixNode.state, ed)) {
return mixNode.g; //g即步数
}
/*对取出的结点进行移动操作,生成新的子节点。*/
/*寻找空格的位置*/
int cx = -1, cy = -1;//cx,cy代表空格的坐标[cx,cy]
arc tmp;int tmps;state_toArc(mixNode.state, tmp);
for (int i = 1; i <= 3; i++) {
if (cx != -1) break;
for (int j = 1; j <= 3; j++) {
if (tmp[i][j] == 0)
{
cx = i;cy = j;
break;
}}}
/*移动生成子结点*/
for (int k = 0; k < 4; k++) {
int nx = cx + move_x[k];
int ny = cy + move_y[k];
if (nx >= 1 && nx <= 3 && ny >= 1 && ny <= 3)//保证移动后的空格不越界
{
swap(tmp[cx][cy], tmp[nx][ny]); //将原来空格和移动后的空格应在的位置的元素,交换顺序
tmps = arc_toState(tmp); //提取出新生成的状态序列state值
swap(tmp[cx][cy], tmp[nx][ny]);//还原序列,用于空格其他方向的移动
/*对新生成的子节点进行查重判定是否入open表中*/
Snode newNode(tmps, mixNode.g + 1, H2(tmps, ed), index++, mixNode.cur);//初始化新生成的子节点
//新生成的子节点的state是tmps,深度是父节点mixNode的深度+1,h用判定函数h(x)求得,序列号按序+1,父节点序列号是mixNode的序列号cur
int newF = F(newNode);//保存新结点的F值
//查找新生成结点的state是否在closed表中
if (!closed.count(tmps))//如果不在closed表中,执行以下操作
{
/*查找新生成结点的state是否在open表中*/
/*双map表,key(f)-value(state),value-key,在查找元素的时候,不用遍历,直接利用low_bound()函数找value-key表中的的first值value*/
map<Snode, int>::iterator it_v = open_value.lower_bound(newNode);
//如果该元素的first值恰好=newNode,说明newNode的序列值state在open表中存在
map<int, Snode>::iterator it_k;//创建指向key-value表迭代器的指针it_k
/*如果在open表中*/
if (it_v != open_value.end() && it_v->first == newNode) {
//如果新生成的结点是相对于原open表中结点的最优解
if ((newNode.g )< ((it_v->first).g)) {
for (it_k = open_key.lower_bound(F(it_v->first)); it_k != open_key.upper_bound(F(it_v->first)); ++it_k)
{
if (it_k->second == newNode) break;//找到open表中重复结点
}
//删除原有open表中结点
open_key.erase(it_k);
open_value.erase(it_v);
//将新结点加入open表中
open_key.insert(make_pair(newF, newNode));
open_value.insert(make_pair(newNode, newF));
}
//不是最优解,放弃新生成的结点
}
//既不在open表中,也不在closed表中
else {
//将新结点加入open表中
open_key.insert(make_pair(newF,newNode));
open_value.insert(make_pair(newNode,newF));
}
}
else if (closed.count(tmps)) //如果在closed表中,执行以下操作
{
//不用判断是否在open表中,因为想先入closed表必须先入open表,想插入一个结点到open表时,如果它已经在closed表中,是不会把它放到open表里的
//close只是一个int状态,Snode结构在path里,故查path
int old;
for (old = 0; old < path.size(); old++) {
if (path[old] == newNode) break;//Snode类型的==号代表state值相同
}
//如果是更优解
if (newNode.g < path[old].g) {
//将原closed表中的元素删除,将新结点放入open表中。新结点的路径在新结点初始化时就已经保存,新结点的f值在加入open表时进行保存
closed.erase(closed.lower_bound(newNode.state));
path.erase(path.begin() + old);
//将新结点加入open表中
open_key.insert(make_pair(newF, newNode));
open_value.insert(make_pair(newNode,newF));
}
//如果不是更优解,舍弃新生成的结点newNode
}
/*对新生成的子节点进行判定是否入open表结束*/
}
}/*对移动生成的新结点的整个操作结束*/
}
//函数走到这里,代表open表为空,则无解,返回步骤-1*/
return -1;//一般不会走到这一步
}
//要从后向前找到最优解的路径,采取的是后序遍历,那必然传递参数有pre,有step(第几步),由于查找时是查找path上的路径,path是依次进栈的方法加入元素
//故pre元素必定在子元素的前面
void findPath(int pre, int size, int step) {
if (step == -1) {
return;
}
else if (step == 0) {
cout << "Step-->" << step << endl;
cout << endl;
arc tmp;
state_toArc(path[size].state, tmp);
outPut(tmp);
cout << endl;
return;
}
for (int i = size; i >= 0; i--) {
//找到path中原结点的pre结点,递归调用函数,输出结果
if (path[i].cur == pre) findPath(path[i].pre, i, step - 1);
}
cout << "Step--> " << step << endl;
cout << endl;
arc tmp;
state_toArc(path[size].state, tmp);
outPut(tmp);
cout << endl;
}
void goPath(int step) {
findPath((path.end() - 1)->pre, path.size() - 1, step);
}
4.main.cpp
#include "stdafx.h"
#include"global.h"
#include"function.h"
#include"windows.h"
#include"ctime"
int main()
{
double time = 0;
double counts = 0;
LARGE_INTEGER nFreq;
LARGE_INTEGER nBeginTime;
LARGE_INTEGER nEndTime;
QueryPerformanceFrequency(&nFreq);
QueryPerformanceCounter(&nBeginTime);//开始计时
/* clock_t start, end;
start = clock();*/
system("color F0");
arc st, ed;
freopen("1.txt", "r+", stdin);
inPut(st);
inPut(ed);
/*cout << "初始矩阵为:\n";
outPut(st);
cout << "目标矩阵为:\n";
outPut(ed);*/
//run(arc_toState(st), arc_toState(ed));
freopen("CON", "r", stdin);//暂停函数之前,使用freopen重定向输入回控制台
/*cout<<"请选择你想使用的评估函数"
int H;cin>>H;*/
int H =1;
int step = run(arc_toState(st), arc_toState(ed),H);
if (step != -1)
{
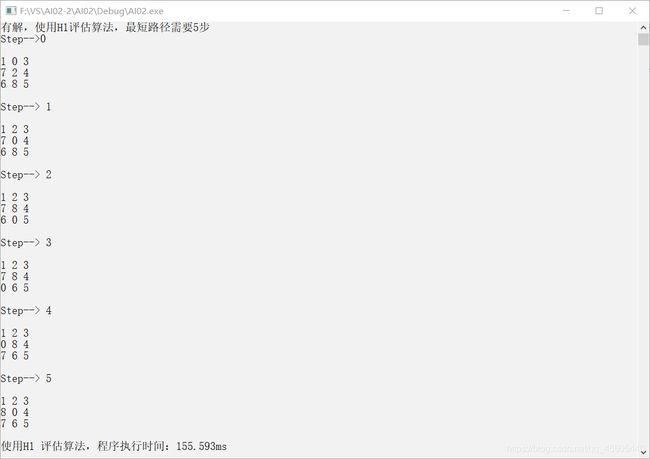
cout << "有解,使用H"<<H<<"评估算法,最短路径需要" << step<<"步" << endl;
goPath(step);
}
else {
cout << "不可达" << endl;
}
//cout << arc_toState(st);
/*end = clock();
cout << "使用H"<
QueryPerformanceCounter(&nEndTime);//停止计时
time = (double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart;//计算程序执行时间单位为s
cout << "使用H" << H << " 评估算法,程序执行时间:" << time * 1000 << "ms" << endl;
freopen("CON", "r", stdin);//暂停函数之前,使用freopen重定向输入回控制台
system("pause");// system("pause>nul");
return 0;
}
5.1.txt
1 0 3 7 2 4 6 8 5
1 2 3 8 0 4 7 6 5
1 3 2 4 0 5 6 7 8
1 2 3 8 0 4 7 6 5
0 1 2 3 4 5 6 7 8
8 0 6 5 4 7 2 3 1
在这个txt里每两行是一个初始状态和目标状态,共设置了三组,一组一组上下变换顺序即可。删除和添加的时候也要一组一组的修改。