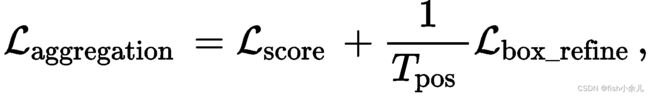(TPAMI 2020) Part-A^2 Net

Abstract

LiDAR点云的3D目标检测是3D场景理解中的一个具有挑战性的问题，具有许多实际应用。在本文中，我们将我们的初步工作PointRCNN扩展到一个新颖且强大的基于点云的3D目标检测框架，即部分感知和聚合神经网络（Part-$A^2$网络）。整个框架由部分感知阶段和部分聚合阶段组成。首先，部分感知阶段首次充分利用从3D ground-truth框派生的free-of-charge部分监督，同时预测高质量的3D proposals和准确的目标内部分位置。同一proposal中预测的目标内部分位置由我们新设计的RoI感知点云池模块分组，从而有效地表示对每个3D proposal的几何特定特征进行编码。然后，部分聚合阶段通过探索池化的目标内部分位置的空间关系来学习对框进行重新评分并细化框位置。进行了广泛的实验以证明我们提出的框架的每个组件的性能改进。我们的Part-$A^2$网络优于所有现有的3D检测方法，并通过仅利用LiDAR点云数据在KITTI 3D目标检测数据集上实现了新的最新技术。代码可在https://github.com/sshaoshuai/PointCloudDet3D获得。

索引词： 3D目标检测、点云、part location、激光雷达、卷积神经网络、自动驾驶。

1 INTRODUCTION

随着自动驾驶和机器人技术的需求激增，3D目标检测受到越来越多的关注[1]，[2]，[3]，[4]，[5]，[6]，[7]，[8]，[9]，[10]，[11]，[12]，[13]。虽然在从图像[14]，[15]，[16]，[17]，[18]，[19]，[20]，[21]，[22]，[23]，[24]中检测2D目标方面已经取得了显著的成就，但是直接将这些2D检测方法扩展到3D检测可能会导致较差的性能，因为3D场景的点云数据具有不规则的数据格式，点云的3D检测面临着不规则数据格式和3D目标6自由度(DoF)的大搜索空间的巨大挑战。

现有的3D目标检测方法已经探索了几种方法来应对这些挑战。一些作品[6]、[25]、[26]利用2D检测器从图像中检测2D框，然后采用PointNet[27]、[28]对裁剪后的点云直接从原始图像回归3D框的参数点云。然而，这些方法严重依赖于2D目标检测器的性能，并且不能利用3D信息的优势来生成鲁棒的边界框proposals。其他一些作品[1]、[4]、[5]、[10]、[11]从鸟瞰图投影点云以创建2D鸟瞰点密度图，并将2D卷积神经网络(CNN)应用于这些特征图用于3D目标检测，但手工制作的特征无法充分利用原始点云的3D信息，可能不是最优的。还有一些one-stage 3D目标检测器[7]、[9]、[29]将3D空间划分为规则的3D体素，并应用3D CNN或3D稀疏卷积[30]、[31]来提取3D特征和最后压缩成鸟瞰特征图以进行3D目标检测。这些工作并没有充分利用3D框注释中的所有可用信息来提高3D检测的性能。例如，3D框标注还暗示了每个3D目标内的点分布，这有利于学习更多的判别特征以提高3D目标检测的性能。此外，这些作品都是one-stage检测框架，不能利用RoI池化方案来汇集每个proposal的特定特征，以便在第二阶段进行框细化。

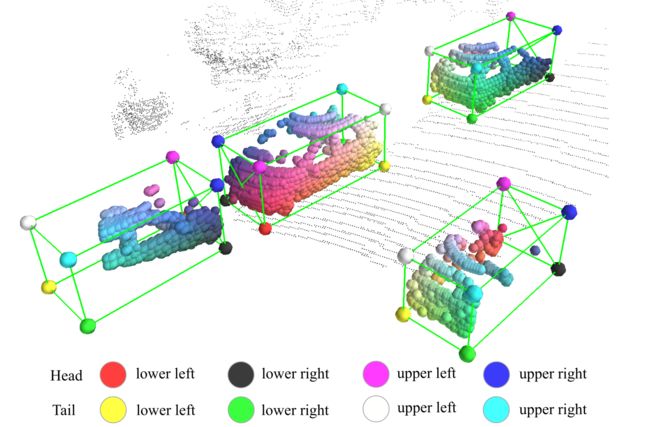
相比之下，我们提出了一种新颖的two-stage 3D目标检测框架，即部分感知和聚合神经网络（即Part-$A^2$网络），它直接在3D点云上运行并实现最先进的3D检测性能通过从训练数据中充分探索信息丰富的3D框注释。我们的主要观察结果是，与2D图像中的目标检测不同，自动驾驶场景中的3D目标由带注释的3D边界框自然且良好地分离，这意味着带有3D框注释的训练数据会自动提供free-of-charge的语义掩码，甚至3D ground truth边界框内每个前景点的相对位置（参见图1的说明）。在本文的其余部分中，每个前景点相对于它所属的目标框的相对位置表示为目标内部分位置。这与2D图像中的框标注完全不同，因为2D图像中目标的某些部分可能被遮挡。使用ground-truth 2D边界框会为目标内的每个像素生成不准确和嘈杂的目标内部分位置。这些3D目标内部件位置暗示了3D目标的3D点分布。这种3D目标内部分位置信息丰富，可以免费获得，但从未在3D目标检测中探索过。

图1. 我们提出的部分感知和聚合网络即使在目标被部分遮挡的情况下也可以准确地预测目标内部分位置。这样的part locations可以帮助准确的3D目标检测。通过我们提出的方法预测的目标内部分位置通过八个角的插值颜色进行可视化。

受此观察的启发，我们提出的Part-$A^2$网络被设计为一种新颖的两阶段3D检测框架，该框架由部分感知阶段（Stage-I）组成，用于预测准确的目标内部分位置和学习逐点特征，以及部分聚合阶段（Stage-II）用于聚合部分信息以提高预测框的质量。我们的方法生成用$(x,y,z,h,w,l,\theta )$参数化的3D边界框，其中$(x,y,z)$是框的中心坐标，$(h,w,l)$是高度、宽度和每个框的长度，$\theta$是从鸟瞰角度看每个框的方位角。

具体来说，在part-aware stage-I中，网络学习分割前景点并估计所有前景点的目标内部分位置（见图1），其中分割掩码和ground-truth部分位置注释直接从ground-truth 3D框注释生成。此外，它还从原始点云生成3D proposals，同时进行前景分割和部分估计。我们研究了两种策略，即anchor-free v.s.基于锚的策略，用于3D proposal生成以处理不同的场景。anchor-free策略相对轻量级，内存效率更高，而基于锚的策略以更多的内存和计算成本实现更高的召回率。对于anchor-free策略，我们建议通过分割前景点并同时从预测的前景点生成3D proposals，以自下而上的方案直接生成3D边界框proposals。由于它避免了像以前的方法[4]、[29]那样在整个3D空间中使用大量3D锚框，因此节省了很多内存。对于基于锚的策略，它从下采样的鸟瞰特征图生成3D proposals，在每个空间位置具有预定义的3D锚框。由于它需要在每个位置放置多个具有不同方向和类别的3D锚点，因此需要更多内存但可以实现更高的目标召回率。

在现有的two-stage检测方法的第二阶段中，需要通过一定的池化操作来聚合3D proposals中的信息，以进行后续的框重新评分和位置细化。然而，之前的点云池化策略（在我们的初步PointRCNN[32]中使用）会导致表示不明确，因为不同的proposals最终可能会池化同一组点，这会失去对proposals的几何信息进行编码的能力。为了解决这个问题，我们提出了一种新颖的可微分RoI感知点云池化操作，它将来自非空体素和空体素的所有信息保留在proposals中，以消除先前点云池化策略的模糊性。这对于获得框评分和位置细化的有效表示至关重要，因为空体素也对框的几何信息进行编码。

stage-II旨在通过提议的RoI感知池聚合stage-I的池化部分特征，以提高proposals的质量。我们的stage-II网络采用稀疏卷积和稀疏池化操作逐步聚合每个3D proposal的池化部分特征，以进行准确的置信度预测和框细化。实验表明，聚合的部分特征可以显着提高proposals的质量，我们的整体框架在KITTI 3D检测基准上实现了最先进的性能。

我们的主要贡献可以概括为四方面。(1)我们提出了用于从点云进行3D目标检测的Part-$A^2$网络框架，该框架通过使用free-of-charge的目标内部分信息来学习有区别的3D特征并通过有效聚合部分特征来提高3D检测性能具有RoI感知池和稀疏卷积。(2)我们提出了两种3D proposal生成策略来处理不同的场景。anchor-free策略的内存效率更高，而基于锚的策略导致更高的目标召回率。(3)我们提出了一种可区分的RoI感知点云区域池化操作，以消除现有点云区域池化操作中的歧义。实验表明，池化特征表示显着有利于框细化阶段。(4)截至2019年8月15日，我们提出的Part-$A^2$网络在具有挑战性的KITTI 3D检测基准[33]上以14 FPS的推理速度以显着的优势优于所有已发表的方法，这证明了我们方法的有效性。

2 RELATED WORK

从2D图像中检测3D目标。 现有几项关于从图像估计3D边界框的工作。[34]、[35]利用3D和2D边界框之间的几何约束来恢复3D目标姿态。[36]、[37]、[38]、[39]利用3D目标和CAD模型之间的相似性。陈等人[40]、[41]将目标的3D几何信息表示为能量函数，以对预定义的3D框进行评分。库等人[42]提出了聚合损失以提高单目图像的3D定位精度。最近[43]、[44]探索了立体图像对以提高立体相机的3D检测性能。由于缺乏准确的深度信息，这些工作只能生成粗略的3D检测结果，并且会受到外观变化的严重影响。

来自多个传感器的3D目标检测。 几种现有的方法已经致力于融合来自多个传感器（例如，激光雷达和相机）的信息，以帮助3D目标检测。[1]、[4]将点云投影到鸟瞰图，并分别从鸟瞰图和图像中提取特征，然后通过将3D proposals投影到相应的2D特征图进行裁剪和融合，以进行3D目标检测。[5]通过提出连续融合层将图像特征融合到鸟瞰特征进一步探索了特征融合策略。与将点云投影到鸟瞰图不同，[6]、[25]利用现成的2D目标检测器首先检测2D框以裁剪点云，然后应用PointNet[27]、[28]提取来自裁剪点云的特征用于3D框估计。这些方法在实际应用中可能存在多个传感器的时间同步问题。与这些传感器融合方法不同，我们提出的3D检测框架Part-$A^2$网络可以通过仅使用点云作为输入来实现相当甚至更好的3D检测结果。

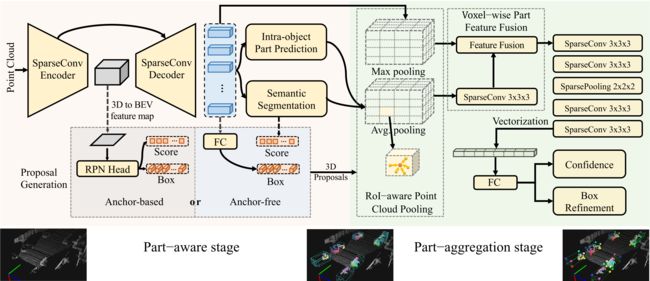
图2.我们用于3D目标检测的部分感知和聚合神经网络的总体框架。它由两个阶段组成：（a）part-aware stage-I首次预测目标内部分位置，并通过将点云馈送到我们的编码器-解码器网络来生成3D proposals。 (b) part-aggregation stage-II进行提议的RoI感知点云池化操作以聚合来自每个3D proposal的部分信息，然后使用part-aggregation网络对框进行评分并根据部件特征和细化位置来自第一阶段的信息。

仅从点云进行3D目标检测。 Zhou等人[29]首次提出VoxelNet架构从点云中学习判别特征并仅用点云检测3D目标。[7]通过引入稀疏卷积[30]、[31]来改进VoxelNet，以实现有效的体素特征提取。[9]、[10]、[11]将点云投影到鸟瞰图，并在这些地图上应用2D CNN进行3D检测。这些方法没有充分利用来自信息丰富的3D框注释的所有可用信息，并且都是one-stage 3D检测方法。相比之下，我们提出的two-stage 3D检测框架Part-$A^2$网络探索3D框注释提供的丰富信息，并学习预测准确的目标内部分位置以学习3D目标的点分布，预测的目标内部分位置在第二阶段聚合用于细化3D proposals，这显着提高了3D目标检测的性能。

用于3D目标检测的点云特征学习。 从点云中学习特征以进行3D检测通常有三种方式。(1)[1],[4],[5],[10],[11]将点云投影到鸟瞰图，并利用2D CNN进行特征提取。(2)[6]、[25]进行PointNet[27]、[28]直接从原始点云中学习点云特征。(3)[29]提出了VoxelNet，[7]应用稀疏卷积[30]、[31]来加速VoxelNet进行特征学习。只有第二种和第三种方法有可能提取逐点特征来分割前景点并预测我们框架中的目标内部分位置。在这里，我们设计了一个与UNet[45]类似的编码器-解码器点云骨干网络来提取有区别的逐点特征，它基于3D稀疏卷积和3D稀疏反卷积操作，因为它们比基于点的方法更高效和有效像PointNet++[28]这样的主干。在第4.1.1节中对基于点的主干和基于体素的主干进行了实验和讨论。

3D/2D实例分割。 这些方法通常基于基于点云的3D检测方法。3D实例分割的几种方法基于3D检测边界框，具有用于预测目标掩码的额外掩码分支。Yi等人[46]提出了一种综合分析策略来生成用于3D实例分割的3D proposals。Hou等人[47]将多视图RGB图像和3D点云相结合，以更好地生成建议并以端到端的方式预测目标实例掩码。

其他一些方法首先估计语义分割标签，然后根据学习的逐点嵌入将点分组为实例。Wang等人[48]计算了点之间的相似度，用于对每个实例的前景点进行分组。Wang等人[49]提出了一种语义感知点级实例嵌入策略，以学习更好的语义和实例点云分割特征。Lahoud等人[50]提出了一个掩码任务学习框架来学习特征嵌入和实例中心的方向信息，以便更好地将点聚类到实例中。然而，他们没有像我们提出的方法那样利用free-of-charge的目标内部件位置作为额外的监督。

还有一些通过将像素聚类到实例中来进行2D实例分割的anchor-free方法。Brabandere等人[51]采用判别损失函数将同一实例的像素聚集在特征空间中，而Bai等人[52]提出估计修改后的分水岭能量景观以分离不同实例的像素。然而，这些方法仅将前景像素/点分组到不同的实例中，并没有估计3D边界框。与上述方法不同，我们提出的anchor-free方法估计目标内部分位置并直接从各个3D点生成3D边界框proposals，以实现3D目标检测。

目标检测的Part模型。 基于可变形Part的模型（DPM）[53]在使用深度学习模型之前在2D目标检测方面取得了巨大成功。[54]、[55]、[56]将DPM扩展到3D世界，以推理3D中的部分并估计目标姿势，其中[54]将目标建模为具有可变形面和可变形部分的3D长方体，[55]提出了一种3D DPM，它生成具有连续外观表示的完整3D目标模型，并且[56]提出了与3D CAD模型共享3D part的概念以估计精细姿态。这些基于DPM的方法通常采用几个经过手工特征训练的部分模板来定位目标并估计目标姿态。相比之下，我们将目标部分表示为点云上下文中的逐点目标内部分位置，其中部分位置的训练标签可以直接从3D框注释生成，并且它们隐式编码3D目标的部分分布。此外，目标内部分位置的估计和聚合都是通过更强大的深度学习网络而不是以前的手工方案来学习的。

3 PART-$A^2$ NET: 3D PART-AWARE AND AGGREGATION FOR 3D DETECTION FROM POINT CLOUD

这项工作的初步版本在[32]中提出，我们提出PointRCNN用于从原始点云进行3D目标检测。为了使框架更加通用和有效，在本文中，我们将PointRCNN扩展到一个新的端到端3D检测框架，即部分感知和聚合神经网络，即Part-$A^2$网络，以进一步提高3D的性能基于点云的目标检测。

关键的观察是，3D目标检测的ground-truth框不仅自动提供准确的分割掩码，因为3D目标在3D场景中自然分离，而且还暗示了ground truth框中每个前景3D点的相对位置。这与2D目标检测非常不同，其中2D目标框可能由于遮挡而仅包含目标的一部分，因此无法为每个2D像素提供准确的相对位置。这些前景点的相对位置编码了前景3D点的有价值信息，有利于3D目标检测。这是因为同一类（如汽车类）的前景目标通常具有相似的3D形状和点分布。前景点的相对位置为框评分和定位提供了强有力的线索。我们将3D前景点相对于其对应框的相对位置命名为目标内部分位置。

这些目标内部分位置为从点云中学习有区别的3D特征提供了丰富的信息，但在以前的3D目标检测方法中从未探索过。有了如此丰富的监督，我们提出了一种新颖的部分感知和聚合3D目标检测器Part-$A^2$网络，用于从点云检测3D目标。具体来说，我们建议使用free-of-charge的3D目标内部分位置标签和分割标签作为额外的监督，以在第一阶段学习更好的3D特征。然后在第二阶段聚合每个3D proposal中的预测3D目标内部分位置和逐点3D特征，以对框进行评分并细化它们的位置。总体框架如图2所示。

图3.自动驾驶场景中体素化点云与原始点云的对比。每个非空体素的中心被认为是形成体素化点云的一个点。体素化的点云大致相当于原始点云，并且3D目标的3D形状很好地保留用于3D目标检测。

3.1 Stage-I: Part-aware 3D proposal generation

部分感知网络旨在通过学习估计前景点的目标内部分位置来从点云中提取判别特征，因为这些部分位置通过指示3D目标表面点的相对位置来隐式编码3D目标的形状。此外，部分感知阶段学习估计前景点的目标内部分位置并同时生成3D proposals。提出了两种从点云生成3D proposal的策略，即anchor-free方案和基于锚的方案，以处理不同的场景。

3.1.1 Point-wise feature learning via sparse convolution

为了分割前景点并估计它们的目标内部分位置，我们首先需要学习用于描述原始点云的判别逐点特征。而不是使用[27]、[28]、[57]、[58]、[59]、[60]、[61]等基于点的方法从点云中提取逐点特征，如图所示图2的左侧部分，我们建议利用具有稀疏卷积和反卷积的编码器-解码器网络[30]、[31]来学习用于前景点分割和目标内部分位置估计的判别逐点特征，这更比我们的初步工作[32]中使用的之前的PointNet++主干网络高效且有效。

具体来说，我们将3D空间体素化为规则体素，并通过堆叠稀疏卷积和稀疏反卷积提取每个非空体素的体素特征，其中每个体素的初始特征简单地计算为每个体素内点坐标的平均值LiDAR坐标系中的体素。每个非空体素的中心被认为是一个点，以形成具有逐点特征（即逐点特征）的新点云，这大约相当于原始点云，如图3所示，因为与整个3D空间（~70m×80m×4m）相比，体素尺寸要小得多（例如，在我们的方法中为5cm×5cm×10cm）。对于KITTI数据集[33]中的每个3D场景，3D空间中通常有大约16,000个非空体素。体素化的点云不仅可以通过更有效的基于稀疏卷积的主干进行处理，而且还可以保持与原始点云大致等价，用于3D目标检测。

我们基于稀疏卷积的主干是基于编码器-解码器架构设计的。输入特征量的空间分辨率通过一系列步长为2的稀疏卷积层下采样8倍，然后通过稀疏反卷积逐渐上采样到原始分辨率，以进行体素特征学习。详细的网络结构在第3.5节和图7中进行了说明。我们新设计的基于3D稀疏卷积的主干在我们的初步PointRCNN框架[32]中比基于PointNet++的主干具有更好的3D框召回率（如表1中的实验结果所示），这证明了这种新主干对于逐点特征学习的有效性。

图4.前景点的目标内部分位置示意图。这里我们使用插值颜色来表示每个点的目标内部分位置。

3.1.2 Estimation of foreground points and intra-object part locations

分割掩码帮助网络区分前景点和背景，而目标内部分位置为神经网络识别和检测3D目标提供了丰富的信息。例如，车辆的侧面通常是与其相应边界框的侧面平行的平面。通过学习不仅可以估计前景分割掩码，还可以估计每个点的目标内部分位置，神经网络发展了推断目标形状和姿态的能力，这对于3D目标检测至关重要。

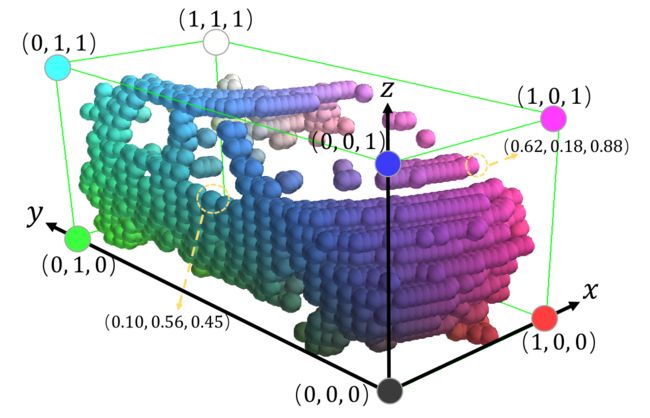
Formulation of intra-object part location. 如图4所示，我们将每个前景点的目标内部分位置表示为其在其所属的3D ground-truth框中的相对位置。我们将三个连续值$\left(x^{(part)},y^{(part)},z^{(part)}\right)$表示为前景点的目标目标内部分位置$\left(x^{(p)},y^{(p)},z^{(p)}\right)$，可以计算如下

$$\begin{array}{rl}\left[x^{(t)}{y}^{(t)}\right]& =\left[x^{(p)}-x^{(c)}{y}^{(p)}-y^{(c)}\right]\left[\begin{array}{cc}\cos (\theta )& \sin (\theta )\\ -\sin (\theta )& \cos (\theta )\end{array}\right],\\ x^{(part)}& =\frac{x^{(t)}}{w}+0.5,y^{(part)}=\frac{y^{(t)}}{l}+0.5,\\ z^{(part)}& =\frac{z^{(p)}-z^{(c)}}{h}+0.5,\end{array}\text{\hspace{1em}(1)}$$

其中$\left(x^{(c)},y^{(c)},z^{(c)}\right)$是框的中心，$(h,w,l)$是框的大小（高度、宽度、长度），$\theta$是鸟瞰图中的框方向。前景点$x^{(\text{part })},y^{(\text{part })},z^{(\text{part })}\in [0,1]$的相对局部位置，因此目标中心的局部位置为$(0.5,0.5,0.5)$。请注意，目标内位置坐标系遵循与KITTI全局坐标系类似的定义，其中$z$的方向垂直于地面，$x$和$y$平行于水平面。

Learning foreground segmentation and intra-object part location estimation. 如图2所示，给定上述基于稀疏卷积的主干，在编码器-解码器主干的输出特征上附加了两个分支，用于分割前景点并预测它们的目标内部分位置。两个分支都使用sigmoid函数作为最后的非线性函数来生成输出。前景点的分割分数表示预测的目标内部分位置的置信度，因为目标内部分位置仅在训练阶段在前景点上定义和学习。由于在大型户外场景中，前景点的数量通常远小于背景点的数量，因此我们采用focal loss[21]来计算点分割损失${\mathcal{L}}_{\mathrm{seg}}$来处理类不平衡问题

$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{seg}}\left(p_t\right)& =-{\alpha }_t{\left(1-p_t\right)}^{\gamma }\log \left(p_t\right)\\ \text{ where }{p}_t& =\{\begin{array}{ll}p& \text{ for forground points }\\ 1-p& \text{ otherwise. }\end{array}\end{array}\text{\hspace{1em}(2)}$$

其中$p$是单个3D点的预测前景概率，我们保持${\alpha }_t=0.25$和$\gamma =2$作为原始论文。ground-truth框内的所有点都被用作正点，其他点被视为训练负点。

为了估计每个前景点的目标内部分位置（表示为$\left(x^{(\text{part })},y^{(\text{part })},z^{(\text{part })}\right)$），因为它们在[0, 1]之间有界，我们应用二进制交叉熵每个前景点的损失如下

$$\begin{array}{rl}{\mathcal{L}}_{\text{part }}\left(u^{(part)}\right)=& -u^{(part)}\log \left({\tilde{u}}^{(part)}\right)\\ & -\left(1-u^{(part)}\right)\log \left(1-{\tilde{u}}^{(part)}\right)\\ & \text{ for }u\in \{x,y,z\}\end{array}\text{\hspace{1em}(3)}$$

其中，${\tilde{u}}^{(part)}$是来自网络输出的预测目标内部分位置，$u^{(\text{part })}$是对应的ground-truth目标内部分位置。请注意，part location估计仅针对前景点进行。

3.1.3 3D proposal generation from point cloud

为了在第二阶段聚合预测的目标内部分位置和学习的逐点3D特征以提高3D目标检测的性能，我们需要生成3D proposals来对属于同一目标的前景点进行分组。在这里，我们研究了两种从点云生成3D proposal的策略，即anchor-free方案和基于锚的方案，以处理不同的场景。anchor-free策略的内存效率更高，而基于锚的策略以更多的内存成本实现更高的召回率。

Anchor-free 3D proposal generation. 我们采用这种策略的模型表示为Part-$A^2$-free。我们提出了一种类似于我们初步的PointRCNN[32]的新方案，以自下而上的方式生成3D proposals。如图2左侧所示，我们在稀疏卷积主干的解码器上附加了一个额外的分支，以从预测为前景的每个点生成3D proposal。

但是，如果算法直接从每个前景点估计目标的中心位置，回归目标（targets）会在很大范围内变化。例如，对于目标角落的前景点，其相对于目标中心的偏移量远大于目标侧面前景点的相对偏移量。如果使用常规回归损失（例如，L1或L2损失）直接预测每个前景点的相对偏移量，则损失将主要由角前景点的误差决定。

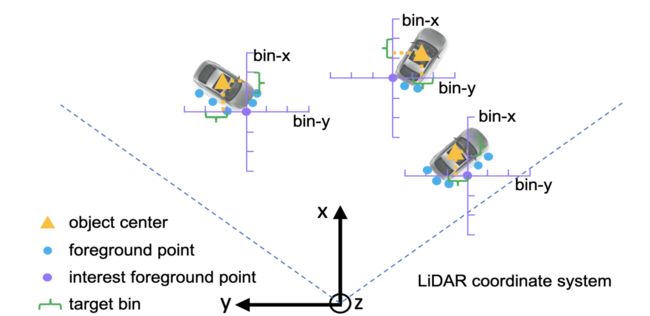
图5.基于bin的中心定位示意图。每个前景点沿$X$和$Y$轴的周围区域被分割成一系列的bin来定位目标中心。

为了解决回归目标变化范围大的问题，我们提出了基于bin的中心回归损失。如图5所示，我们通过将每个轴的搜索范围$\mathcal{S}$划分为长度一致$\delta$的bin，将每个前景点的周围鸟瞰区域沿$X$和$Y$轴划分为一系列离散的 bin，代表不同的$X-Y$平面上的目标中心$(x,y)$。我们观察到，使用$X$和$Y$轴的交叉熵损失进行基于bin的分类，而不是使用平滑L1损失[14]进行直接回归，可以实现更准确和稳健的中心定位。为了在分配到每个$X-Y$ bin之后细化小的定位，还估计了一个小的残差。因此，$X$轴或$Y$轴的总体回归损失由bin分类损失和分类bin内的残差回归损失组成。对于沿垂直$Z$轴的中心位置$z$，我们直接使用smooth-L1损失进行回归，因为大多数目标的$z$值通常在非常小的范围内。因此，目标中心回归目标可以表述为

$${\mathrm{bin}}_x^{(p)}=\lfloor \frac{x^{(c)}-x^{(p)}+\mathcal{S}}{\delta }\rfloor ,{\mathrm{bin}}_y^{(p)}=\lfloor \frac{y^{(c)}-y^{(p)}+\mathcal{S}}{\delta }\rfloor .$$
$${\mathrm{res}}_{u\in \{x,y\}}^{(p)}=\frac{1}{\delta }\left(u^{(c)}-u^{(p)}+\mathcal{S}-\left({\mathrm{bin}}_u^{(p)}\cdot \delta +\frac{\delta }{2}\right)\right),\text{\hspace{1em}(4)}$$
$${\mathrm{res}}_z^{(p)}=z^{(c)}-z^{(p)}$$

其中$\delta$是bin大小，$\mathcal{S}$是搜索范围，$\left(x^{(p)},y^{(p)},z^{(p)}\right)$是前景兴趣点的坐标，$\left(x^{(c)},y^{(c)},z^{(c)}\right)$是其对应目标的中心坐标，${\mathrm{bin}}_x^{(p)}$和${\mathrm{bin}}_y^{(p)}$ 是ground-truth bin分配，${\mathrm{res}}_x^{(p)}$和${\mathrm{res}}_y^{(p)}$是ground-truth残差在指定的bin内进一步细化位置。

由于我们提出的自下而上的proposal生成策略是anchor-free，它没有框方向的初始值。因此我们直接将方向$2\pi$划分为bin大小为$w$的离散bin，并计算bin分类目标${\mathrm{bin}}_{\theta }^{(p)}$和残差回归目标${\mathrm{res}}_{\theta }^{(p)}$为

$$\begin{array}{rl}{\mathrm{bin}}_{\theta }^{(p)}& =\lfloor \frac{\left(\theta +\frac{w}{2}\right)\mathrm{mod}2\pi }{\omega }\rfloor ,\\ {\mathrm{res}}_{\theta }^{(p)}& =\frac{2}{\omega }\left(\left(\left(\theta +\frac{w}{2}\right)\mathrm{mod}2\pi \right)-\left({\mathrm{bin}}_{\theta }^{(p)}\cdot \omega +\frac{\omega }{2}\right)\right),\end{array}\text{\hspace{1em}(5)}$$

因此，整体3D边界框回归损失$L_{box}$可以表示为

$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{bin}}^{(p)}& =\sum _{u\in \{x,y,\theta \}}\left({\mathcal{L}}_{\mathrm{ce}}\left({\mathrm{bin}}_u^{(p)},{\mathrm{bin}}_u^{(p)}\right)+{\mathcal{L}}_{\mathrm{smooth}-\mathrm{L}1}\left({\mathrm{res}}_u^{(p)},{\mathrm{res}}_u^{(p)}\right)\right),\\ {\mathcal{L}}_{\text{res }}^{(p)}& =\sum _{v\in \{z,h,w,l\}}{\mathcal{L}}_{\mathrm{smooth}-\mathrm{L}1}\left({\mathrm{res}}_v^{(p)},{\mathrm{res}}_v^{(p)}\right),\\ {\mathcal{L}}_{\mathrm{box}}& ={\mathcal{L}}_{\mathrm{bin}}^{(p)}+{\mathcal{L}}_{\text{res }}^{(p)},\end{array}\text{\hspace{1em}(6)}$$

其中${\mathrm{bin}}_u(p)$和${\mathrm{bin}}_u(p)$是前景点$p$的预测bin分配和残差，${\mathrm{bin}}_u^{(p)}$和${\mathrm{res}}_u^{(p)}$是如上计算的ground-truth目标，${\mathrm{res}}_v^{(p)}$是预测的纵轴中心残差或相对于整个训练集中每个类的平均目标大小的大小残差，${\mathrm{res}}_v^{(p)}$是${\mathrm{res}}_v^{(p)}$对应的ground-truth目标，$L_{ce}$表示交叉熵分类损失，${\mathcal{L}}_{\text{smooth-L1 }}$表示${\mathcal{L}}_{\text{smooth-L1 }}$损失。请注意，框回归损$L_{box}$仅适用于前景点。

在推理阶段，通过首先选择预测置信度最高的bin中心，然后添加预测残差，得到回归的$x、y$和$\theta$。

基于这种anchor-free策略，我们的方法不仅充分探索了来自点云的3D信息以生成3D proposal，而且通过限制仅生成3D proposal，避免在3D空间中使用大量预定义的3D锚框。通过前景点。

Anchor-based 3D proposal generation. 我们采用这种策略的模型表示为Part-$A^2$-anchor。stage-I如图2所示，基于稀疏卷积的编码器采用形状为$M\times N\times H$的体素化点云，并产生一个8次X轴和Y轴下采样的$\frac{M}{8}\times \frac{N}{8}$ 2D鸟瞰特征图，它具有$\frac{H}{16}\times D$特征通道，其中$\frac{H}{16}$表示沿Z轴下采样16次的特征量，$D$是每个编码特征体素的特征维度，$“\times D”$表示在每个x−y不同高度的鸟瞰位置，得到一维特征向量。然后，我们将与[7]类似的区域提议网络(RPN)头附加到上述鸟瞰特征图，用于使用预定义的3D锚点生成3D proposal。每个类有$2\times \frac{M}{8}\times \frac{N}{8}$个预定义的锚点，每个类都有指定的锚点大小，其中鸟瞰特征图上的每个像素都有一个平行于X轴的锚点和一个平行于Y轴的锚点。每个类都有自己的预定义锚点，因为不同类的目标大小差异很大。例如，在KITTI数据集上，我们对汽车使用$(l=3.9,w=1.6,h=1.56)$米，对行人使用$(l=0.8,w=0.6,h=1.7)$米，对骑自行车的人使用$(l=1.7,w=0.6,h=1.7)$米。

通过计算2D鸟瞰联合交叉点(IoU)将锚点与ground-truth框相关联，其中正IoU阈值根据经验设置为0.6、0.5、0.5，负IoU阈值分别为汽车、行人和骑自行车者的0.45、0.35、0.35。我们将两个核大小为$1\times 1\times 1$的卷积层添加到鸟瞰特征图，用于proposal分类和框回归。我们使用类似于等式2的焦点损失。(2)对于锚点评分，对于正面锚点直接使用基于残差的回归损失。这里，我们直接采用常用的平滑L1损失进行回归，因为由于IoU阈值，锚和它们对应的ground-truth框之间的中心距离通常在比anchor-free策略的中心距离更小的范围内。利用候选锚$\left(x^{(a)},y^{(a)},z^{(a)},h^{(a)},w^{(a)},l^{(a)},{\theta }^{(a)}\right)$和目标ground truth $\left(x^{(gt)},y^{(gt)},z^{(gt)},h^{(gt)},w^{(gt)},l^{(gt)},{\theta }^{(gt)}\right)$，中心、角度和大小的基于残差的框回归目标被定义为

$$\begin{array}{rl}& \Delta x^{(a)}=\frac{x^{(gt)}-x^{(a)}}{d^{(a)}},\Delta y^{(a)}=\frac{y^{(gt)}-y^{(a)}}{d^{(a)}},\Delta z^{(a)}=\frac{z^{(gt)}-z^{(a)}}{h^{(a)}}\\ & \Delta l^{(a)}=\log \left(\frac{l^{(gt)}}{l(a)}\right),\Delta h^{(a)}=\log \left(\frac{h^{(gt)}}{h^{(a)}}\right),\Delta w^{(a)}=\log \left(\frac{w^{(gt)}}{w^{(a)}}\right)\\ & \Delta {\theta }^{(a)}=\sin \left({\theta }^{(gt)}-{\theta }^{(a)}\right),\text{ where }{d}^{(a)}=\sqrt{{\left(l^{(a)}\right)}^2+(w^{(a){)}^2}}\end{array}\text{\hspace{1em}(7)}$$

其中，方向目标编码为$\sin \left({\theta }^{(gt)}-{\theta }^{(a)}\right)$，以消除方向循环值的模糊性。然而，这种方法将两个相反的方向编码为相同的值，因此我们采用一个核大小为$1\times 1\times 1$的额外卷积层到鸟瞰特征图，如[7]中所示，用于分类两个相反的方向，其中方向目标通过以下方法计算:如果${\theta }^{(gt)}$为正，则方向目标为1，否则方向目标为0(注意，${\theta }^{(gt)}\in [-\pi ,\pi )$)。我们使用的交叉熵损失类似于等式(3)。对于取向方向的二元分类，这被表示为术语$L_{dir}$。那么总的3D边界框回归损失$L_{box}$可以表示为
$${\mathcal{L}}_{\text{box }}=\sum _{\text{res }\in \{x,y,z,l,h,w,\theta \}}{\mathcal{L}}_{\text{smooth-L1 }}\left(\Delta {\text{ res }}^{(a)},\Delta {\text{ res }}^{(a)}\right)+\beta {\mathcal{L}}_{\text{dir }}\text{\hspace{1em}(8)}$$

其中$\Delta \mathrm{res}(a)$是候选anchor的预测残差，${\mathrm{\Delta res}}^{(a)}$是如公式(7)计算的相应的ground-truth目标，损失权重$\beta =0.1$。请注意，框回归损失$L_{box}$仅适用于正锚。

Discussion of the two 3D proposal generation strategies. 这两种3D proposal生成策略都有其优点和局限性。所提出的anchor-free策略通常是轻量级和内存高效的，因为它不需要在3D空间中的每个空间位置评估大量锚。多类目标检测的效率更为明显，因为3D目标检测中的不同类别通常需要不同的锚框，而anchor-free方案可以共享逐点特征来生成多个类别的proposals。第二种基于锚的proposal生成策略通过使用每个类的预定义锚覆盖整个鸟瞰图特征图来实现稍高的召回率，但具有更多参数并需要更多GPU内存。详细的实验和比较在4.1.4节中讨论。

3.2 RoI-aware point cloud feature pooling

给定预测的目标内部件位置和3D proposals，我们的目标是通过聚合部分信息和学习同一proposal中所有点的逐点特征来进行框评分和proposal细化。在本小节中，我们首先介绍canonical变换以减少不同3D proposals的旋转和位置变化的影响，然后我们提出RoI-aware点云特征池化模块以消除先前点云池化操作的模糊性并编码用于框细化的3D proposal的位置特定特征。

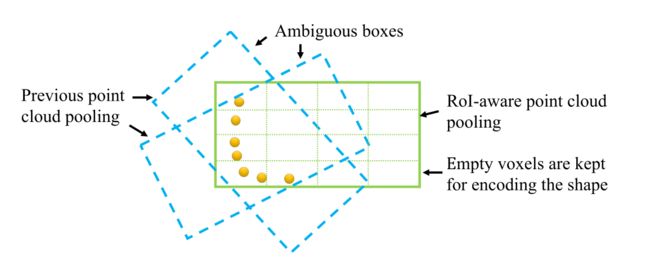
图6.提议的RoI感知点云特征池的图示。之前的点云池化方法无法有效地编码提案的几何信息（蓝色虚线框）。我们提出的RoI感知点云池化方法可以通过保留空体素来编码框的几何信息（绿色框），这可以通过以下稀疏卷积进行有效处理。

Canonical transformation. 我们观察到，如果框细化目标在规范坐标系中归一化，则可以通过以下框细化阶段更好地估计。我们将属于每个proposal的池化点转换为相应3D proposal的单个规范坐标系。一个3D proposal的规范坐标系表示：（1）原点位于box proposal的中心；(2)局部$X^{\prime }$和$Y^{\prime }$轴与地平面近似平行，其中$X^{\prime }$指向proposal的头部方向，另一个$Y^{\prime }$轴垂直于$X^{\prime }$；(3)$Z^{\prime }$轴与全局坐标系保持一致。box proposal的所有池化点的坐标$p$应通过适当的旋转和平移转换为规范坐标系为$\tilde{p}$。正的3D proposals及其对应的ground-truth 3D框也被转换为规范坐标系，以计算用于框细化的残差回归目标。所提出的规范坐标系基本上消除了不同3D proposals的大量旋转和位置变化，并提高了特征学习的效率，以用于以后的框位置细化。

RoI-aware point cloud feature pooling. 我们的初步工作PointRCNN[32]中的点云池化操作只是将3D proposals中的点状特征池化，其对应的点位置在3D proposal内。所有内部点的特征都由PointNet++编码器聚合，用于在第二阶段细化proposal。然而，我们观察到这个操作丢失了很多3D几何信息，并在不同的3D proposals之间引入了歧义。这种现象如图6所示，其中不同的proposals会产生相同的汇集点。相同的池化特征对接下来的细化阶段产生了不利影响。

因此，我们提出了RoI感知点云池化模块，将每个3D proposal均匀地划分为具有固定空间形状$\left(L_x\times L_y\times L_z\right)$的规则体素，其中$L_x,L_y,L_z$是每个池化分辨率的整数超参数3D proposal的尺寸（例如，我们的框架采用$14\times 14\times 14$）并且独立于不同的3D proposal大小。

具体而言，令$\mathcal{F}=\left\{f_i\in {\mathbb{R}}^{C_0},i\in 1,\cdots ,n\right\}$表示3D proposal $\mathbf{b}$中所有内部点的逐点特征，它们根据3D proposal分散在3D proposal的分割体素中到它们的局部规范坐标$\mathcal{X}=\left\{\left(x_i^{(ct)},y_i^{(ct)},z_i^{(ct)}\right)\in {\mathbb{R}}^3,i\in 1,\cdots ,n\right\}$，其中$n$是内部点的数量。然后RoI感知体素最大池化和平均池化操作可以表示为

$$Q=\mathrm{RoIAwareMaxPool}(\mathcal{X},\mathcal{F},\mathbf{b}),Q\in {\mathbb{R}}^{L_x\times L_y\times L_z\times C_0}\text{\hspace{1em}(9)}$$

$$Q=\mathrm{RoIAwareAvgPool}(\mathcal{X},\mathcal{F},\mathbf{b}),Q\in {\mathbb{R}}^{L_x\times L_y\times L_z\times C_0}\text{\hspace{1em}(10)}$$

其中$Q$是proposal $\mathbf{b}$的池化3D特征量。具体来说，体素最大池化和平均池化的第$k$个体素$Q_k$处的特征向量可以计算为

$$Q_k=\{\begin{array}{ll}\max \left\{f_i\in {\mathcal{N}}_k\right\}& \text{ if }\left|{\mathcal{N}}_k\right|>0\\ 0& \text{ if }\left|{\mathcal{N}}_k\right|=0\end{array}\text{\hspace{1em}(11)}$$
or
$$Q_k=\{\begin{array}{ll}\frac{1}{|{\mathcal{N}}_k|}{\sum }_i{f}_i,f_i\in {\mathcal{N}}_k& \text{ if }\left|{\mathcal{N}}_k\right|>0\\ 0& \text{ if }\left|{\mathcal{N}}_k\right|=0\end{array}$$

其中${\mathcal{N}}_k$是属于第$k$个体素的点集，$k\in \left\{1,\cdots ,L_x\times L_y\times L_z\right\}$。请注意，此处空体素($\left|{\mathcal{N}}_k\right|=0$)的特征将设置为零并标记为空，以用于以下基于稀疏卷积的特征聚合。

所提出的RoI感知点云池化模块对具有相同局部空间坐标的不同3D proposals进行编码，其中每个体素对3D proposal框中相应固定网格的特征进行编码。这种特定于位置的特征池可以更好地捕捉3D proposal的几何形状，并为后续框评分和位置细化提供有效的表示。此外，所提出的RoI感知池化模块是可微的，这使得整个框架可以端到端训练。

3.3 Stage-II: Part location aggregation for confidence prediction and 3D box refinement

通过考虑在stage-I的3D框propsoal中预测的目标内部分位置的空间分布和学习的逐点部分特征，将proposal中的所有信息聚合起来以进行框提案评分和细化是合理的。基于汇集的3D特征，我们训练一个子网络以稳健地聚合信息以对框proposals进行评分并优化其位置。

Fusion of predicted part locations and semantic part features. 如图2右侧所示，我们采用提出的RoI感知点云池化模块来获得每个3D proposal的判别特征。令$\mathbf{b}$表示单个3D proposal，并且对于它的所有内部点（标准坐标$\mathcal{X}=\left\{\left(x_i^{(ct)},y_i^{(ct)},z_i^{(ct)}\right)\in {\mathbb{R}}^3,i\in 1,\cdots ,n\right\}$)，我们将${\mathcal{F}}_1=\left\{\left(x_i^{(\text{part })},y_i^{(\text{part })},z_i^{(\text{part })},s_i\right)\in {\mathbb{R}}^4,i\in 1,\cdots ,n\right\}$表示为他们的预测点-来自第一阶段逐点的部分位置和语义分数，并表示${\mathcal{F}}_2=\left\{f_i^{(\mathrm{sem})}\in {\mathbb{R}}^C,i\in 1,\cdots ,n\right\}$作为骨干网络学习的它们的逐点语义部分特征。这里$n$是proposal $\mathbf{b}$的内部点的总数。那么proposal $\mathbf{b}$的part feature encoding可以表述为

$$\begin{array}{rl}{Q}^{(\text{part })}& =\mathrm{RoIAwareAvgPool}\left(\mathcal{X},{\mathcal{F}}_1,\mathbf{b}\right)\\ Q^{(\text{sem })}& =\mathrm{RoIAwareMaxPool}\left(\mathcal{X},{\mathcal{F}}_2,\mathbf{b}\right)\\ Q_k^{(roi)}& =\left[G\left(Q_k^{(\text{part })}\right),Q_k^{(\text{sem })}\right],k\in \left\{1,\cdots ,L_x\times L_y\times L_z\right\}\end{array}\text{\hspace{1em}(12)}$$

其中$G$表示子流形稀疏卷积层，用于将池化部分位置转换为相同的特征维度$C$以匹配$Q^{(\mathrm{sem})}$，$[\cdot ,\cdot ]$表示特征连接。这里$Q^{(part)}$、$Q^{(sem)}$和$Q^{(roi)}$具有相同的空间形状（默认为$14\times 14\times 14$）。融合特征$Q^{(roi)}$通过骨干网络对proposals提议的几何和语义信息进行编码。请注意，这里我们使用平均池化池化预测的目标内部分位置${\mathcal{F}}_1$以获得proposal的每个体素的代表性预测部分位置，而我们使用最大池化池化语义部分特征${\mathcal{F}}_2$。

Sparse convolution for part information aggregation. 对于每个3D proposal，我们需要从该proposal的所有内部空间位置聚合融合特征$Q^{(roi)}$，以实现稳健的框评分和细化。如图2右侧所示，我们堆叠了几个内核大小为$3\times 3\times 3$的3D稀疏卷积层，以随着接受域的增加聚合proposal的所有部分特征。在这里，我们还在稀疏卷积层之间插入了一个内核大小为$2\times 2\times 2$和步幅为2的稀疏最大池化，以将特征量下采样到$7\times 7\times 7$，以节省计算成本和参数。最后，我们将其向量化为特征向量（空体素保持为零）并将其输入两个分支以进行框评分和位置细化。

与直接将池化3D特征量向量化为特征向量的简单方法相比，我们基于稀疏卷积的部分聚合策略可以通过从局部到全局尺度聚合特征来有效地学习预测部分位置的空间分布。稀疏卷积策略还通过节省大量计算、参数和GPU内存来实现更大的 $14\times 14\times 14$池化大小。

3D IoU guided box scoring. 对于stage-II的框评分分支，受[35]、[62]的启发，我们将3D proposal与其对应的ground truth框之间的3D Intersectoin-overUnion(IoU)标准化为proposal质量评估的软标签。proposal质量$q^{(a)}$定义为
$$q^{(a)}=\{\begin{array}{ll}1& \text{ if }\mathrm{IoU}>0.75\\ 0& \text{ if }\mathrm{IoU}<0.25\\ 2\mathrm{IoU}-0.5& \text{ otherwise }\end{array}\text{\hspace{1em}(13)}$$

这也由类似于等式（3）定义的二元交叉熵损失$L_{score}$监督。我们在4.1.7节的实验表明，与传统的基于分类的框评分相比，IoU引导框评分的性能略好一些。

3.4 Overall loss

我们的整个网络是端到端可训练的，整体损失函数由部分感知损失和部分聚合损失组成。

Losses of part-aware stage-I. 对于part-aware stage-I，损失函数由三个具有相同损失权重的项组成，包括前景点分割的focal loss、part locations回归的二元交叉熵损失和3D proposal生成的smooth-L1 loss，

$${\mathcal{L}}_{\text{aware }}={\mathcal{L}}_{\text{seg }}+\frac{1}{N_{\text{pos }}}{\mathcal{L}}_{\text{part }}+\lambda \frac{1}{M_{\text{pos }}}{\mathcal{L}}_{\text{box }}\text{\hspace{1em}(14)}$$

其中损失权重$\lambda =2.0$，$N_{pos}$是前景点的总数，$M_{\text{pos }}=N_{\text{pos }}$ 对于 Part-A2-free模型，$M_{pos}$是Part-A2-anchor模型的正锚总数。对于$L_{box}$损失，如3.1.3节中所述， Part-A2-free采用基于bin的box generation loss，Part-A2-anchor模型采用residual-based box regression loss。

图7. Part-A2-anchor模型的part-aware stage-I的基于稀疏卷积的编码器-解码器骨干网络。

Losses of part-aggregation stage-II. 对于部分聚合stage-II，损失函数包括用于框质量回归的二元交叉熵损失项和用于3D框proposal细化的平滑L1损失项，

其中$T_{\text{pos }}$是正proposals的数量，我们对等式（7）中使用的$L_{box}$细化进行了基于残差的框回归损失，其中包括框中心细化损失、尺寸细化损失和角度细化损失。除此之外，我们还添加了 [6] 中使用的角正则化损失$L_{corner}$，最终框细化损失如下

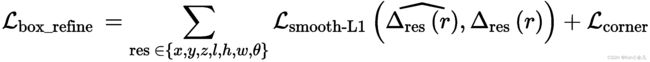
其中 $\Delta {\mathrm{res}}^{(r)}$是3D proposal的预测残差，$\Delta {res}^{(r)}$是与等式(7)类似计算的相应ground-truth目标，并且这里的所有损失具有相同的损失权重。请注意，这里的角度细化目标直接编码为$\Delta {\theta }^{(r)}=\left({\theta }^{(gt)}-{\theta }^{(r)}\right)$，因为由于IoU，proposal与其对应的ground-truth框之间的角度差在一个很小的范围内positive proposal的约束。

Overall loss. 因此，我们用于端到端训练的Part-$A^2$网络的整体损失函数计算为
$${\mathcal{L}}_{\text{total }}={\mathcal{L}}_{\text{aware }}+{\mathcal{L}}_{\text{aggregation }}\text{\hspace{1em}(17)}$$

其中这两个阶段的损失具有相等的损失权重。

3.5 Implementation details

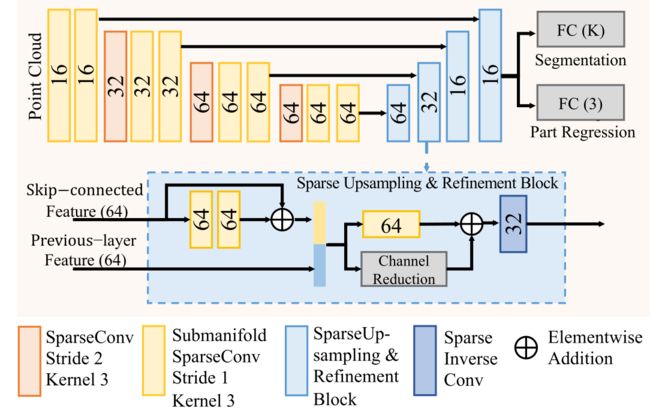
我们设计了一个类似UNet的架构[45]，用于在获得的稀疏体素上使用3D稀疏卷积和3D稀疏反卷积来学习逐点特征表示。通过三个步长为2的稀疏卷积对空间分辨率进行8次下采样，每个卷积后面跟着几个子流形稀疏卷积。如图7所示，我们还设计了一个与[63]中类似的上采样块，基于稀疏操作来细化融合特征。

Network details. 如图7所示，对于$\mathrm{Part}-A^2$-anchor模型的part-aware stage-I，空间特征量有四个尺度，特征维度为16-32-64-64，我们使用三个带核的3D稀疏卷积层大小$3\times 3\times 3$和步长为2将空间分辨率下采样8倍。我们在每个级别堆叠两个子流形卷积层，内核大小为$3\times 3\times 3$，步长为1。解码器中有四个稀疏上采样块（网络细节见图7），以逐渐增加特征维度为64-64-32-16。注意最后一个上采样块的步长为1，其他三个上采样块的步长为2。对于Part-A2-free网络，我们将解码器在每个尺度上的特征维度增加到128，并使用简单连接以融合来自同一级别编码器和前一层解码器的特征，因为解码器的学习点特征应该为自下而上的3D proposal生成编码更多的判别特征。

对于part-aggregation阶段，如图2所示，RoI-aware点云池化模块的池化大小为$14\times 14\times 14$，经过稀疏卷积和max-pooling处理后下采样为$7\times 7\times 7$特征维度为128。我们将下采样的特征量向量化为单个特征向量，用于最终的框评分和位置细化。

Training and inference details. 我们使用ADAM优化器和批量大小6对50个epoch进行端到端的整个网络训练。cosine annealing学习率策略用于初始学习率0.001。我们从每个场景中随机选择128个建议用于训练stage-II，具有1:1的正负proposals，其中用于框细化的正proposals具有3D IoU，其对应的ground truth框对于所有类至少为0.55，否则为负proposals，评分目标定义为方程式(13)用于置信度预测。

我们在训练期间进行常见的数据增强，包括随机翻转、使用从[0.95, 1.05]均匀采样的缩放因子的全局缩放、围绕垂直轴的全局旋转一个从$\left[-\frac{\pi }{4},\frac{\pi }{4}\right]$均匀采样的角度。为了模拟具有各种环境的目标，如[7]，我们还从其他场景随机“copy”了几个带有内部点的ground-truth框，并将它们“paste”到当前训练场景。我们提出的部分感知和部分聚合网络的整个训练过程在单个NVIDIA Tesla V100 GPU上大约需要17个小时。

对于推理，只有100个提案保留在part-aware stage-I中，$\mathrm{Part}-A^2-$free的NMS阈值为0.85，Part-$A^2$-anchor的NMS阈值为0.7，然后通过以下part-aggregation stage-II对其进行评分和细化。我们最终应用阈值为0.01的旋转NMS来去除冗余框并生成最终的3D检测结果。单张Tesla V100 GPU卡上的整体推理时间约为70毫秒。

3.6 Pros and cons.

我们提出的3D 目标检测框架在不同情况下具有一些优点和缺点。

与之前的3D目标检测方法相比[1]、[4]、[5]、[6]、[7]、[26]、[29]、[64]，（1）我们首次提出的方法引入了目标内部分位置的学习，以提高从点云检测3D目标的性能，其中预测的目标内部分位置有效地编码了3D目标的点分布，有利于3D目标检测。(2)提出的RoI-aware特征池化模块消除了先前点云池化操作的模糊性，将稀疏的逐点特征转换为规则体素特征，对3D proposals的特定位置几何和10个语义特征进行编码，有效地桥接了proposal生成网络和提案细化网络，并导致高检测精度。(4)此外，part locations的学习过程也可以用于其他任务，以学习更具辨别力的逐点特征，例如点云的实例分割。所提出的RoI感知池化模块也可以灵活地用于将基于点的网络（例如PointNet++）的逐点特征转换为稀疏体素特征，这些特征可以由更有效的稀疏卷积网络处理。

另一方面，我们的方法也有一些局限性。由于我们的方法针对自动驾驶场景中的高性能3D目标检测，我们方法的某些部分不能很好地应用于室内场景的3D目标检测。这是因为室内场景中的3D边界框可能会相互重叠（例如桌下的椅子），因此室内场景的3D边界框标注无法提供准确的逐点分割标签。此外，有些类别的方向没有明确定义（例如round tables），因此我们无法生成提议的目标内部分位置的准确标签。

然而，我们提出的anchor-free proposal生成策略在室内场景的3D proposal生成方面仍然显示出巨大的潜力，因为室内目标不总是停留在地面上，并且我们的anchor-free策略避免了在整个3D空间中设置3D锚。

5 CONCLUSION

在本文中，我们将我们的初步工作PointRCNN扩展到一个新的3D检测框架，即部分感知和聚合神经网络(Part-$A^2$ net)，用于从原始点云中检测3D目标。我们的部分感知stage-I学习通过使用来自ground-truth 3D框注释的free-of-charge目标内位置标签和前景标签来估计准确的目标内part locations。同时，3D proposals由两种备选策略生成，anchor-free方案和基于锚方案。通过新颖的RoI感知的点云汇集方案来汇集每个目标的预测的目标内部分位置。接下来的part-aggregation stage-II可以更好地捕捉目标部件的几何信息，以准确地对框进行评分并细化它们的位置。

我们的方法明显优于现有的3D检测方法，并在具有挑战性的KITTI 3D检测基准上实现了新的最先进的性能。广泛的实验被精心设计和进行，以研究我们提出的框架的各个组成部分。

REFERENCES

[1] X. Chen, H. Ma, J. Wan, B. Li, and T. Xia, “Multi-view 3d object detection network for autonomous driving,” in CVPR, 2017.

[2] S. Song and J. Xiao, “Sliding shapes for 3d object detection in depth images,” in European conference on computer vision. Springer, 2014, pp. 634–651.

[3] ——, “Deep sliding shapes for amodal 3d object detection in rgb-d images,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 808–816.

[4] J. Ku, M. Mozifian, J. Lee, A. Harakeh, and S. Waslander, “Joint 3d proposal generation and object detection from view aggregation,” IROS, 2018.

[5] M. Liang, B. Yang, S. Wang, and R. Urtasun, “Deep continuous fusion for multi-sensor 3d object detection,” in ECCV, 2018.

[6] C. R. Qi, W. Liu, C. Wu, H. Su, and L. J. Guibas, “Frustum pointnets for 3d object detection from rgb-d data,” arXiv preprint arXiv:1711.08488, 2017.

[7] Y . Yan, Y . Mao, and B. Li, “Second: Sparsely embedded convolutional detection,” Sensors, vol. 18, no. 10, p. 3337, 2018.

[8] X. Du, M. H. Ang, S. Karaman, and D. Rus, “A general pipeline for 3d detection of vehicles,” in 2018 IEEE International Conference on Robotics and Automation (ICRA), May 2018, pp. 3194–3200.

[9] A. H. Lang, S. V ora, H. Caesar, L. Zhou, J. Yang, and O. Beijbom, “Pointpillars: Fast encoders for object detection from point clouds,” CVPR, 2019.

[10] B. Yang, M. Liang, and R. Urtasun, “Hdnet: Exploiting hd maps for 3d object detection,” in 2nd Conference on Robot Learning (CoRL), 2018.

[11] B. Yang, W. Luo, and R. Urtasun, “Pixor: Real-time 3d object detection from point clouds,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 7652–7660.

[12] W. Luo, B. Yang, and R. Urtasun, “Fast and furious: Real time end-to-end 3d detection, tracking and motion forecasting with a single convolutional net,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 3569–3577.

[13] M. Simony, S. Milzy, K. Amendey, and H.-M. Gross, “Complex-yolo: an euler-region-proposal for real-time 3d object detection on point clouds,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 0–0.

[14] R. Girshick, “Fast r-cnn,” in Proceedings of the IEEE international conference on computer vision, 2015, pp. 1440–1448.

[15] S. Ren, K. He, R. Girshick, and J. Sun, “Faster r-cnn: Towards real-time object detection with region proposal networks,” in Advances in neural information processing systems, 2015, pp. 91–99.

[16] W. Liu, D. Anguelov, D. Erhan, C. Szegedy, S. Reed, C.-Y . Fu, and A. C. Berg, “Ssd: Single shot multibox detector,” in European conference on computer vision. Springer, 2016, pp. 21–37.

[17] J. Redmon, S. Divvala, R. Girshick, and A. Farhadi, “Y ou only look once: Unified, real-time object detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 779– 788.

[18] J. Redmon and A. Farhadi, “Y olo9000: better, faster, stronger,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 7263–7271.

[19] T.-Y . Lin, P . Dollár, R. Girshick, K. He, B. Hariharan, and S. Belongie, “Feature pyramid networks for object detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 2117–2125.

[20] J. Dai, H. Qi, Y . Xiong, Y . Li, G. Zhang, H. Hu, and Y . Wei, “Deformable convolutional networks,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 764–773.

[21] T.-Y . Lin, P . Goyal, R. Girshick, K. He, and P . Dollár, “Focal loss for dense object detection,” IEEE transactions on pattern analysis and machine intelligence, 2018.

[22] H. Law and J. Deng, “Cornernet: Detecting objects as paired keypoints,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 734–750.

[23] K. He, G. Gkioxari, P . Dollár, and R. Girshick, “Mask r-cnn,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2961–2969.

[24] Z. Cai and N. V asconcelos, “Cascade r-cnn: Delving into high quality object detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 6154–6162.

[25] D. Xu, D. Anguelov, and A. Jain, “Pointfusion: Deep sensor fusion for 3d bounding box estimation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 244–253.

[26] Z. Wang and K. Jia, “Frustum convnet: Sliding frustums to aggregate local point-wise features for amodal 3d object detection,” in IROS. IEEE, 2019.

[27] C. R. Qi, H. Su, K. Mo, and L. J. Guibas, “Pointnet: Deep learning on point sets for 3d classification and segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 652–660.

[28] C. R. Qi, L. Yi, H. Su, and L. J. Guibas, “Pointnet++: Deep hierarchical feature learning on point sets in a metric space,” in Advances in Neural Information Processing Systems, 2017, pp. 5099–5108.

[29] Y . Zhou and O. Tuzel, “V oxelnet: End-to-end learning for point cloud based 3d object detection,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 4490–4499.

[30] B. Graham and L. van der Maaten, “Submanifold sparse convolutional networks,” arXiv preprint arXiv:1706.01307, 2017.

[31] B. Graham, M. Engelcke, and L. van der Maaten, “3d semantic segmentation with submanifold sparse convolutional networks,” CVPR, 2018.

[32] S. Shi, X. Wang, and H. Li, “Pointrcnn: 3d object proposal generation and detection from point cloud,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 770–779.

[33] A. Geiger, P . Lenz, and R. Urtasun, “Are we ready for autonomous driving? the kitti vision benchmark suite,” in Conference on Computer Vision and Pattern Recognition (CVPR), 2012.

[34] A. Mousavian, D. Anguelov, J. Flynn, and J. Koˇsecká, “3d bounding box estimation using deep learning and geometry,” in Computer Vision and Pattern Recognition (CVPR), 2017 IEEE Conference on. IEEE, 2017, pp. 5632–5640.

[35] B. Li, W. Ouyang, L. Sheng, X. Zeng, and X. Wang, “Gs3d: An efficient 3d object detection framework for autonomous driving,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 1019–1028.

[36] F. Chabot, M. Chaouch, J. Rabarisoa, C. Teulière, and T. Chateau, “Deep manta: A coarse-to-fine many-task network for joint 2d and 3d vehicle analysis from monocular image,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit.(CVPR), 2017, pp. 2040–2049.

[37] M. Zhu, K. G. Derpanis, Y . Yang, S. Brahmbhatt, M. Zhang, C. Phillips, M. Lecce, and K. Daniilidis, “Single image 3d object detection and pose estimation for grasping,” in Robotics and Automation (ICRA), 2014 IEEE International Conference on. IEEE, 2014, pp. 3936–3943.

[38] R. Mottaghi, Y . Xiang, and S. Savarese, “A coarse-to-fine model for 3d pose estimation and sub-category recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, pp. 418–426.

[39] F. Manhardt, W. Kehl, and A. Gaidon, “Roi-10d: Monocular lifting of 2d detection to 6d pose and metric shape,” in Computer Vision and Pattern Recognition (CVPR). IEEE, 2019.

[40] X. Chen, K. Kundu, Z. Zhang, H. Ma, S. Fidler, and R. Urtasun, “Monocular 3d object detection for autonomous driving,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 2147–2156.

[41] X. Chen, K. Kundu, Y . Zhu, A. G. Berneshawi, H. Ma, S. Fidler, and R. Urtasun, “3d object proposals for accurate object class detection,” in Advances in Neural Information Processing Systems, 2015, pp. 424–432.

[42] J. Ku*, A. D. Pon*, and S. L. Waslander, “Monocular 3d object detection leveraging accurate proposals and shape reconstruction,” in CVPR, 2019.

[43] P . Li, X. Chen, and S. Shen, “Stereo r-cnn based 3d object detection for autonomous driving,” in CVPR, 2019.

[44] Y . Wang, W.-L. Chao, D. Garg, B. Hariharan, M. Campbell, and K. Weinberger, “Pseudo-lidar from visual depth estimation: Bridging the gap in 3d object detection for autonomous driving,” in CVPR, 2019.

[45] O. Ronneberger, P . Fischer, and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241.

[46] L. Yi, W. Zhao, H. Wang, M. Sung, and L. J. Guibas, “Gspn: Generative shape proposal network for 3d instance segmentation in point cloud,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 3947–3956.

[47] J. Hou, A. Dai, and M. Nießner, “3d-sis: 3d semantic instance segmentation of rgb-d scans,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 4421–4430.

[48] W. Wang, R. Y u, Q. Huang, and U. Neumann, “Sgpn: Similarity group proposal network for 3d point cloud instance segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 2569–2578.

[49] X. Wang, S. Liu, X. Shen, C. Shen, and J. Jia, “Associatively segmenting instances and semantics in point clouds,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 4096–4105.

[50] J. Lahoud, B. Ghanem, M. Pollefeys, and M. R. Oswald, “3d instance segmentation via multi-task metric learning,” arXiv preprint arXiv:1906.08650, 2019.

[51] B. D. Brabandere, D. Neven, and L. V . Gool, “Semantic instance segmentation with a discriminative loss function,” CoRR, vol. abs/1708.02551, 2017. [Online]. Available: http://arxiv.org/abs/1708. 02551

[52] M. Bai and R. Urtasun, “Deep watershed transform for instance segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 5221–5229.

[53] P . F. Felzenszwalb, R. B. Girshick, D. McAllester, and D. Ramanan, “Object detection with discriminatively trained part-based models,” IEEE transactions on pattern analysis and machine intelligence, vol. 32, no. 9, pp. 1627–1645, 2009.

[54] S. Fidler, S. Dickinson, and R. Urtasun, “3d object detection and viewpoint estimation with a deformable 3d cuboid model,” in Advances in neural information processing systems, 2012, pp. 611–619.

[55] B. Pepik, P . Gehler, M. Stark, and B. Schiele, “3d 2 pm–3d deformable part models,” in European Conference on Computer Vision. Springer, 2012, pp. 356–370.

[56] J. J. Lim, A. Khosla, and A. Torralba, “Fpm: Fine pose parts-based model with 3d cad models,” in European conference on computer vision. Springer, 2014, pp. 478–493.

[57] Q. Huang, W. Wang, and U. Neumann, “Recurrent slice networks for 3d segmentation of point clouds,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 2626–2635.

[58] Y . Li, R. Bu, M. Sun, W. Wu, X. Di, and B. Chen, “Pointcnn: Convolution on x-transformed points,” in Advances in Neural Information Processing Systems, 2018, pp. 820–830.

[59] S. Wang, S. Suo, W.-C. Ma, A. Pokrovsky, and R. Urtasun, “Deep parametric continuous convolutional neural networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 2589–2597.

[60] H. Zhao, L. Jiang, C.-W. Fu, and J. Jia, “Pointweb: Enhancing local neighborhood features for point cloud processing,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 5565–5573.

[61] W. Wu, Z. Qi, and L. Fuxin, “Pointconv: Deep convolutional networks on 3d point clouds,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019, pp. 9621–9630.

[62] B. Jiang, R. Luo, J. Mao, T. Xiao, and Y . Jiang, “Acquisition of localization confidence for accurate object detection,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 784– 799.

[63] S. Sun, J. Pang, J. Shi, S. Yi, and W. Ouyang, “Fishnet: A versatile backbone for image, region, and pixel level prediction,” in Advances in Neural Information Processing Systems, 2018, pp. 762–772.

[64] M. Liang*, B. Yang*, Y . Chen, R. Hu, and R. Urtasun, “Multi-task multisensor fusion for 3d object detection,” in CVPR, 2019.

[65] KITTI 3D object detection benchmark leader board, http://www.cvlibs.net/datasets/kitti/eval object.php?obj benchmark=3d, Accessed on 2019-08-15.