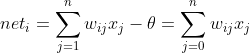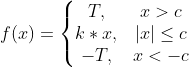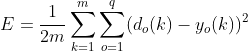神经网络算法基本原理及其实现
目录
背景知识
人工神经元模型
激活函数
网络结构
工作状态
学习方式
BP算法原理
算法实现(MATLAB)
背景知识
在我们人体内的神经元的基本结构,相信大家并不陌生,看完下面这张图,相信大家都能懂
什么是人工神经网络?
人工神经网络是具有适应性的简单神经元组成的广泛并互连的网络,它的组织能够模拟生物神经系统对真实世界物体作出的交互式反应。人工神经网络具有自学习、自组织、较好的容错性和优良的非线性逼近能力。
人工神经网络能干什么?
1、拟合数据——>预测
2、分类——>聚类分析
那么我们学习人工神经网络需要知道哪些呢?
1、神经元模型
2、激活函数
3、网络结构
4、工作状态
5、学习方式
人工神经元模型
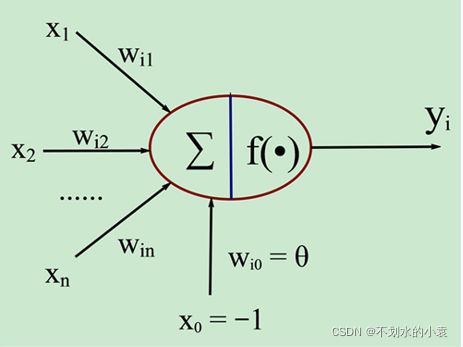
作为神经网络的基本元素,神经元的模型如下:
![]() 是从其他神经元上传来的信号,
是从其他神经元上传来的信号,![]() 表示从神经元
表示从神经元 ![]() 到神经元
到神经元![]() 的连接权值,
的连接权值,![]() 表示一个阈值,或者称为偏置。
表示一个阈值,或者称为偏置。
激活函数
激活函数是对净激活量与输出进行映射的函数。一些常用的激活函数,由于输入数据与期望之间可能并不是量级一样,所以需要激活,激活函数:![]()
一些常用的激活函数有:
线性函数: S型函数:
阈值函数: 双极S型函数:
网络结构
根据网络中神经元的互连方式,可以分为3种神经网络
1、前馈神经网络:在训练的过程中会有反馈信号,而在分类的过程中只能向前传递数据,直到到达输出层,层间没有向后反馈信号
2、反馈神经网络:从输入到输出具有反馈连接的神经元
3、自组织网络:通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构
工作状态
1、学习:利用学习算法来调整神经元之间的连接权值,使得网络输出更符合实际
2、工作:神经元的连接权值不变,可作为分类器或者预测数据时使用
学习方式
1、有导师学习:将一组训练集送入网络,根据网络的实际输出与期望输出间的差别来调整连接权,如BP算法(本文的代码实现也为BP神经网络的算法实现)
2、无导师学习:抽取样本集合中蕴含的统计特性,并以神经元之间的连接权的形式存在于网络中,如(Hebb学习率)
BP算法原理
假设输入层有n个神经元,隐含层有p个神经元,输出层有q个神经元
符号定义:
| 输入向量 | |
| 隐含层输入向量 | |
| 隐含层输出向量 | |
| 输出层输入向量 | |
| 输出层输出向量 | |
| 期望输出向量 | |
| 误差函数 |  |
第一步:计算各层神经元的输入和输出:
第二步:利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数。
第三步:利用隐含层到输出层的连接权值、输出层的![]() 和隐含层的输出计算误差函数对隐含层各神经元的偏导数
和隐含层的输出计算误差函数对隐含层各神经元的偏导数![]()
第四步:利用输出层各神经元的 ![]() 和隐含层各神经元的输出来修正连接权值
和隐含层各神经元的输出来修正连接权值![]()
是设置的学习率
第五步:利用隐含层各神经元的![]() 和输入层各神经元的输入修正连接权
和输入层各神经元的输入修正连接权
第六步:计算全局误差
第七步:判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。否则,选取下一个学习样本及对应的期望输出,返回进入下一轮学习。
算法实现(MATLAB)
注意:由于MATLAB有内置函数可以调用,所以没有从公式原理上从头搭建代码
%BP神经网络
clear all
clc
X=-1:0.1:1;
D=[-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609...
0.1336 -0.2013 -0.4344 -0.5000 -0.3930 -0.1647 -.0988...
0.3072 0.3960 0.3449 0.1816 -0.312 -0.2189 -0.3201];
net = newff(minmax(X),[5 1],{'tansig','tansig'}, 'trainlm');%隐含层5个神经元,输出层1个神经元
net.trainParam.epochs = 10000; %训练的最大次数
net.trainParam.goal = 1e-5; %全局最小误差
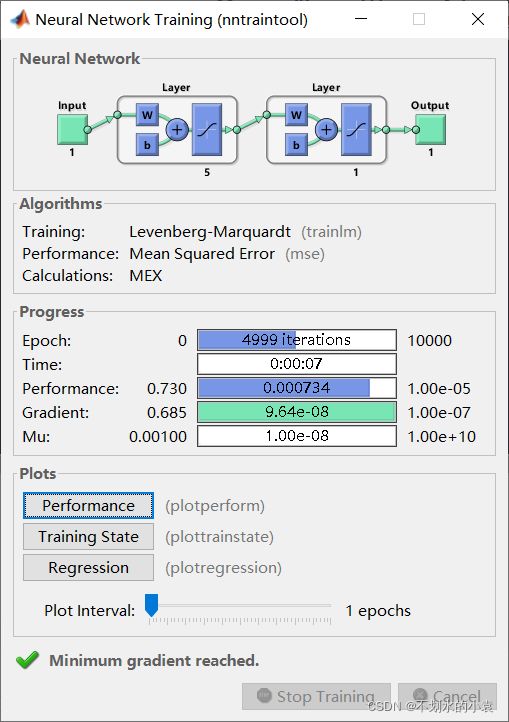
net = train(net,X,D);
O = sim(net,X); %仿真模拟
figure;
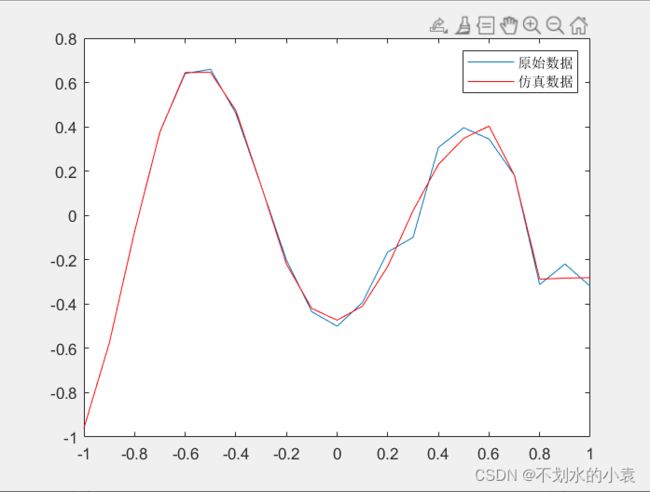
plot(X,D,X,O,'r'); %绘制训练后得到的结果和误差曲线
legend('原始数据','仿真数据')
V = net.iw{1,1}%输入层到中间层权值
theta1 = net.b{1}%中间层各神经元阈值
W = net.lw{2,1}%中间层到输出层权值
theta2 = net.b{2}%输出层各神经元阈值
%%以下是计算结果
V =
63.2827
-21.7727
-19.3926
4.2953
1.7695
theta1 =
-44.7043
7.6890
2.1589
1.4575
2.2024
W =
-0.3473 -0.2570 -0.2184 -1.3224 6.1471
theta2 =
-5.2381仿真的结果:
从以上结构可以看出,这个神经网络训练的还是比较好的,仿真的结果误差很小 。
以上就是BP神经网络的全部推理及实现过程,希望能你有所帮助,谢谢观看!