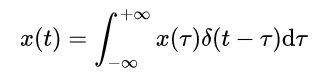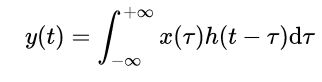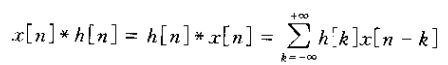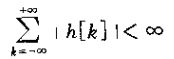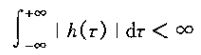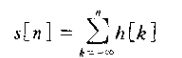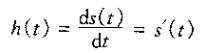线性时不变系统
注：本博客是基于奥本海姆的《信号与系统》第二版编写，主要是为了自己考研，准备专业课。
(转载：https://blog.csdn.net/Explorer_day/article/details/79380955)
一、离散时间线性时不变系统：卷积和
一）、用脉冲表示离散时间信号
1、如何把任何离散时间时间信号看成由离散时间单位脉冲构成的关键是：要把一个离散时间信号当成一串单个脉冲来想象。
2、离散时间单位脉冲序列的筛选性质。
二）、离散时间线性时不变系统的单位脉冲响应及卷积和表示
1、一个线性系统在时刻n的响应就是在时间上每一点的输入值所产生的各个响应在该时刻n的叠加。
2、对于线性时不变系统而言：
这个结果称为卷积和或叠加和，并且右边的运算称为x[n]和h[n]的卷积，并用符号记为：
此式意味着一个很重要的结果——既然一个线性时不变系统对任意输入的响应可以用系统对单位，脉冲的响应来表示，那么线性时不变系统的单位脉冲就完全刻画了系统的特征。
3、求卷积和的方法：将信号x[k]和h[n-k]都看成k的函数，将它们相乘就得到序列g[k]=x[k]h[n-k]，它可看成在每一个时刻k，输入x[k]对输出在时刻k的做出的奉献，这样就可以得到结论——将全部g[k]序列中的眼本质相加就是在所选定的时刻n的输出值。
二、连续时间线性时不变系统：卷积积分
一）、用冲激表示连续时间信号
1、把任意一个连续时间信号看成加权和移位脉冲的叠加。
2、连续时间冲激函数的筛选性质：
二）、连续时间线性时不变系统的单位冲激响应及卷积积分表示
1、对于线性时不变系统而言：
上式称为卷积积分或叠加积分。此表明了一个连续时间线性时不变系统的特性可以用他的单位冲激来刻画。两个信号x(t)和h(t)的卷积，以后就表示成：
可以看到，与离散时间信号下相同，一个连续时间线性时不变系统是完全由它的冲激响应，即对单一的基本信号单位冲激的响应来表征的。
2、卷积积分的求法
为了求出对某一给定t时的这个积分值，首先需要得到
。其实t的函数，t为某一固定值，利用h(t)的反转再加上平移（t>0时就像右移，t<0时就向左移），就可以求得
然后将x(t)与
相乘，将该乘积在t=-∞到t+∞区间内积分就得到y(t)。
三、线性时不变的性质
一）交换律性质
1、在连续时间和离散时间情况下，卷积运算的一个基本能行之是：它满足交换律
1）、在离散时间情况下有：
2）、在连续时间情况下有：
二）、分配律性质
1）、卷积另一个性质是：它满足分配律
1）、在离散时间情况下有：
2）、在连续时间下有：
三）、结合律性质
1、卷积另一个重要而有用的性质是它满足结合律
1）、在离散时间情况下有：
2）、在连续时间情况下有：
四）、有记忆和无记忆线性时不变系统
1、若一个系统在任何时刻的输出仅与同一时刻的输入值有关，它就是无记忆的。
2、如果一个离散时间线性时不变系统h(t)，在n≠0时h[n]=0，则该系统系统就是无记忆的。反之，h[n]对于n≠0不全为零，这个系统就是有记忆的。
3、如果一个连续时间线性时不变系统h(t)，在t≠0时h(t)=0，则该系统系统就是无记忆的。反之，h(t)对于t≠0不全为零，就是有记忆系统。
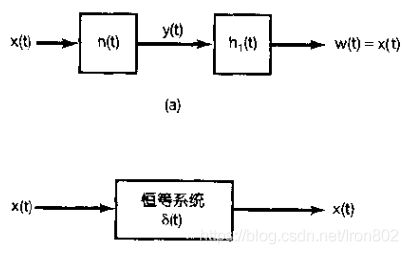
五）、线性时不变系统的可逆性
1、仅当存在一个逆系统，其与原系统级联后所产生的输出等于第一个新系统的输入时，这个系统才是可逆的。而且，如果一个线性时不变系统是可逆的，那么它就有一个线性时不变的逆系统。
2、在连续时间情况下，一个冲激响应为h(t)的线性时不变系统的逆系统的冲激系统h1(t)瞒住以下条件：
3、在离散时间情况下，一个冲激响应为h[n]的线性时不变系统的逆系统的冲激系统h1[n]瞒住以下条件：
六）、线性时不变系统的因果性
1、一个因果系统的输出只取决于现在和过去的输入值。
2、一个离散时间线性时不变系统若要使因果的，其冲激响应应满足下面条件：
3、一个连续时间线性时不变系统若要使因果的，其冲激响应应满足下面条件：
4、一个线性时不变系统的因果性就等效于它的冲激响应是一个因果信号。
七）、线性时不变系统的稳定性
1、如果一个系统对于每一个有界的输入，其输出信号都是有界的，就称该系统是稳定的。
2、在离散时间情况下，如果单位脉冲响应是绝对可和的，即：
那么y[n]就是有界的，因此系统是稳定的。
3、在连续时间情况下，如果单位脉冲响应是绝对可积的，即：
那么y(t)就是有界的，因此系统是稳定的。
八）、线性时不变系统的单位阶跃响应
1、单位阶跃响应s[n]或s(t)也常用来描述一个线性时不变系统的特性，s[n]或s(t)是当x[n]=u[n]或x(t)=u(t)时的系统输出响应。
2、一个离散时间线性时不变系统的单位阶跃响应是其单位脉冲响应的求和函数：
一个离散时间线性时不变系统的单位脉冲响应是其单位阶跃响应的一次差分：
3、一个连续时间线性时不变系统的单位阶跃响应是其单位脉冲响应的积分函数：
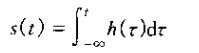
一个连续时间线性时不变系统的单位脉冲响应是其单位阶跃响应的一阶导数：
