机器学习sklearn----KMeans评估指标

引言

前面介绍了KMeans的基础知识。了解了KMeans的基础用法。但是具体需要怎么来评估我们的模型还是一个未知数。今天这节我们会介绍再不考虑实际需求的情况下来评估我们的KMeans模型。实际的应用中是按照我们的需求来评估模型聚类效果的。

数据准备

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline
warnings.filterwarnings("ignore") # 忽略警告

# 创建数据集
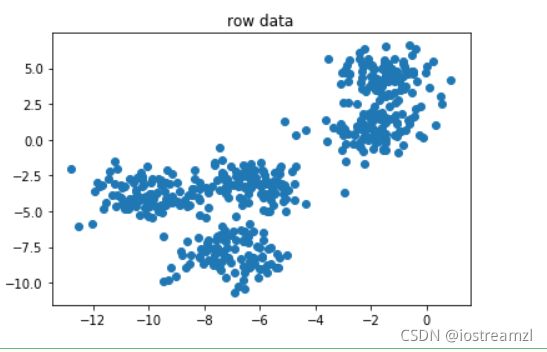
X, y = make_blobs(n_samples = 500, n_features=2, centers=5, random_state=1)
plt.scatter(X[:, 0], X[:, 1])
plt.title("row data")

inertia指标

inertia表示的是每个样本点到其所在质心的距离之和。按照inertia的定义来说inertia是越小越好。 但是实际上我们可以发现当分簇的数量越来越多的时候inertia的值自然越来越小。 甚至再极端的情况下，簇的数量等于样本数的时候，每一个样本就是一个簇，那么inertia就为0。 所以说inertia虽然是一个不错的珩琅标准，单数却很难界定界限在哪里。
示例：查看inertia随n_clusters的变化

# 查看inertia随着n_clusters的变化
for n in range(1, 10) :
    km = KMeans(n_clusters=n)
    km.fit(X, y)
    print("n_clusters: {}\tinertia: {}".format(n, km.inertia_))

# 可以看出inertia的值是越来越小的。但是我们观察原始数据
# 显然分为2-5类是最好的结果，所以这里的inertia作为指标不太适用

轮廓系数silhouette_score

轮廓系数用两个指标来同时评估样本的簇内差异和簇间差异
轮廓系数的计算公式如下：
$$s=\frac{b-a}{max(a,b)}$$
其中 a 表示样本与它所在的簇之间样本的相似性，等于样本与同一簇之间的其他样本的平均距离

b 表示样本与其他簇的相似新，等于样本与离其最近的簇的所有样本的平均距离

我们希望簇内差异小，簇间差异大。那么就是希望b大于a，且越大越好。

轮廓系数s的取值再-1,1之间，s越靠近1越好

from sklearn.metrics import silhouette_score, silhouette_samples
# silhouette_score 返回所有样本的轮廓系数的均值
# silhouette_samples 返回每个样本的轮廓系数

# inertia和轮廓系数的对比
inertia_scores = []
sil_scores = []
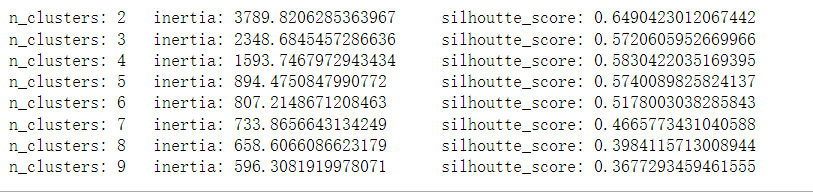
for n in range(2, 10) :
    km = KMeans(n_clusters=n).fit(X, y)
    
    inertia_scores.append(km.inertia_)
    
    # 轮廓系数接收的参数中，第二个参数至少有两个分类
    sc = silhouette_score(X, km.labels_)
    sil_scores.append(sc)
    print("n_clusters: {}\tinertia: {}\tsilhoutte_score: {}".format(
        n, km.inertia_, sc))

可以看到再分为2簇，4簇的时候我们的聚类效果是比较好的，且轮廓系数并不是一个无界的评估指标.