蒙特卡洛方法简单应用（python实现）

算法原理介绍

当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。
实际上，蒙特卡洛方法的理论支撑其实是概率论或统计学中的大数定律。基本原理简单描述是先大量模拟，然后计算一个事件发生的次数，再通过这个发生次数除以总模拟次数，得到想要的结果。下面我们以几个简单应用来学习下蒙特卡洛算法思想。

应用

1.计算圆周率$\pi$

如下图

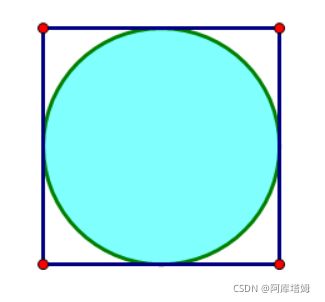
我们向单位正方形中投掷一个点，则其落入单位圆内的概率为$\frac{\pi }{4}$，下面通过程序，产生若干随机点，计算其与中心点的距离是否大于0.5来判断是否位于圆内，模拟此过程求出频率，进而计算$\pi$的值

import numpy as np

m = 10**7#随机点数

x = np.random.random(m)
y = np.random.random(m)

t = 0#计数单位

for i in range(0,m):
    if (x[i]-0.5)**2+(y[i]-0.5)**2<=1/4:#与中心点距离小于半径，位于圆内
        t = t+1

print(4*t/m)#pi=4*t/m

输出结果为3.1411264，由此我们可见，此种方法的收敛速度是比较慢的，这也是蒙特卡洛方法的缺点之一。因此在应用时，一般只对难以应用解析方法求解的过程采用该算法

2.计算积分

利用蒙特卡洛方法可以计算定积分、多重积分，方法是在一定空间中随机产生若干点，用位于被积函数图像下方且在积分区域内的点数除以总点数再乘上一定空间的“体积”，即为所求值，下面具体说明

（1）定积分

求$${\int }_1^2{x}^2\mathrm{d}x$$
如图
在矩形ABCD内随机产生若干点，再计算位于曲线下方的数目，用频率乘ABCD面积即得定积分值

import numpy as np

m = 10**6#随机点数

x = np.random.random(m)
x = x+1
y = np.random.random(m)
y = 4*y

t = 0#计数单位

for i in range(0,m):
    if y[i]<=x[i]**2:#该点位于曲线下方
        t = t+1

print(t*4/m)

结果为2.329988，我们知道精确结果为$\frac{7}{3}$，则已基本解决该问题

（2）多重积分

以三重积分为例$$\int \int {\int }_{V}f\mathrm{d}V$$其中V为$z=\sqrt{x^2+y^2}与z=1$围起来的区域，$f=x^2+y^2+z^2$
积分区域为圆锥内部，如图

容易得出$f=x^2+y^2+z^2$的最大值为2。对于三重积分，类比定积分的过程，产生随机点的空间应为一个“四维立方体”，它各个维度的长度为：x方向，2；y方向，2；z方向，1；w方向，2 。

import numpy as np

m = 10**6
#定义被积函数
def f(x,y,z):
    return x**2+y**2+z**2
#定义积分区域函数
def g(x,y):
    return np.sqrt(x**2+y**2)
#产生随机点
x = np.random.random(m)
x = 2*x-1#x范围（-1,1）
y = np.random.random(m)
y = 2*y-1
z = np.random.random(m)
w = np.random.random(m)
w = 2*w
#计算频率，输出结果
t = 0

for i in range(0,m):
    if z[i]>=g(x[i],y[i]) and w[i]<=f(x[i],y[i],z[i]):
        t=t+1
print(t*8/m)

输出结果为0.946328，通过其他方法得出的更精确的结果为0.9424777960816141

我们可以看出，用该方法计算多重积分的好处是不必要先将问题演化成$${\int }_a^b\mathrm{d}z{\int }_c^d\mathrm{d}y{\int }_e^{f}g(x,y,z)\mathrm{d}x$$的形式，但其需要计算$g(x,y,z)$在积分区域上的最大值。

3.计算函数最值

求函数$$f(x)=sin(7x)\cdot e^{3x}$$在（0,1）上的最小值及取到最小值的点

import numpy as np

m = 10**6

def f(u):
    return np.sin(7*u)*np.exp(3*u)

x = 0
y = 0

for i in range(0,m):
    x_0 = np.random.random_sample()
    if f(x_0)<y:
        x = x_0
        y = f(x_0)
print(x,y)

结果为：0.7310397438065227， -8.238423249137401
该段函数的图像如图：

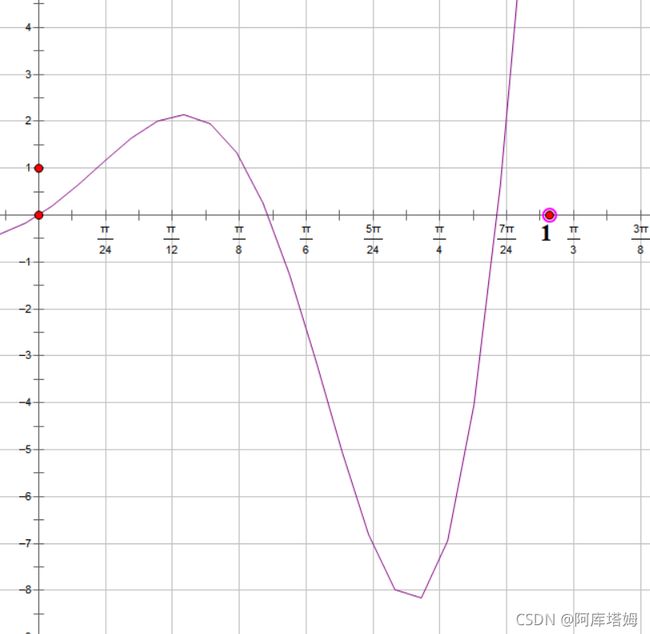
对比可知已近似求得结果

除了以上简单数学问题外，蒙特卡洛方法在金融工程学， 宏观经济学，生物医学，计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算、核工程)等领域应用广泛，是需要好好学习的一种方法。