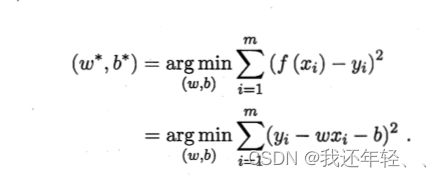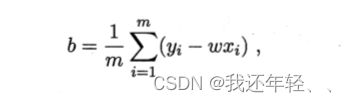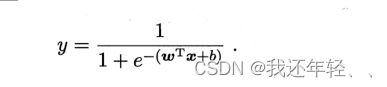西瓜书第三章—— 线性模型
1.1基本形式
线性模型 (linear model) 试图学得一个通过属性的线性组合来进行
预测的函数,即
或者向量形式
其中当w和b确认后,模型就得以确定。
1.2线性回归
给定一个数据集,试图学得一个线性模型,尽可能的预测出真实准确的值作为输出标记。
有数据集后,将其放入线性回归模型,去获取w和b。如何获取又是一个重点。
上图运用了欧氏距离,基于均方误差最小化来进行模型求解,求取w和b使得上图最小化的过程,称为线性回归模型的最小二乘“参数估计”,分别对其进行求导置零,可以求出最优解。
类似可以将其应用于更大的数据集,多维矩阵中。
1.3 对数几率回归
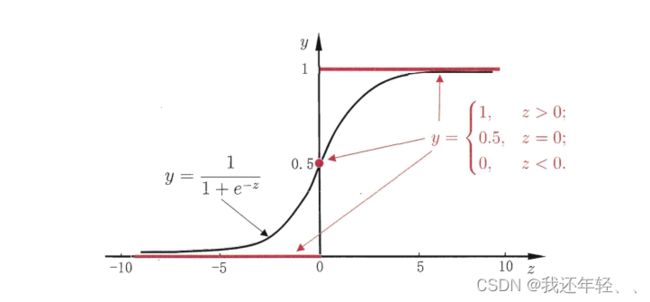
在二分类任务中,输出为{0,1},线性回归模型的产生是实值,将其等比转换为{0/1},是最理想的“单位阶跃函数”。
如果预测值大于0,判为正例,小于0,判为反例,如下图所示。
于是我们希望找到能在一定程度上近似单位阶跃函数的“替代函数” (surrogate function), 并希望它单调可微.对数几率函数 (logisticfunction) 正是这样一个常用的替代函数:
对数几率函数是一种 "Sigmoid 函 数 "它 将 z 值转化为一个接近 0 或 1 的 g 值,并且其输出值在 z = 0 附近变化很陡.将对数几率函数作为代入式, 得到
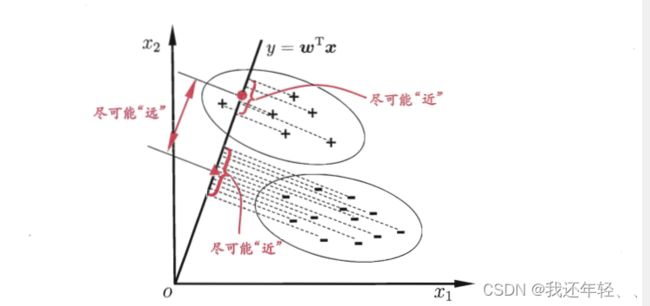
1.4 线性判别分析
线性判别分析(LDA)是一种经典的学习方法,将给定的数据集尽可能的投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。
1.5 多分类学习
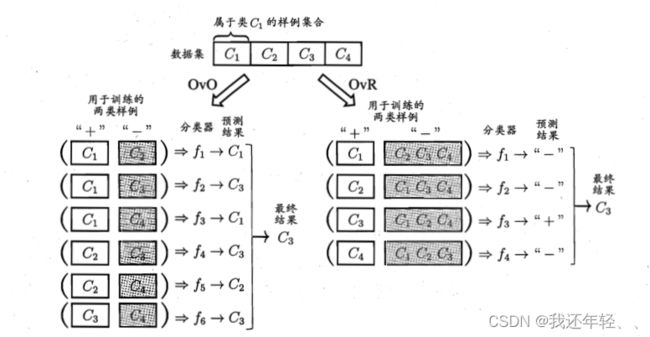
将二分类学习方法可直接推广到多分类, 多分类学习的基本思路是“拆解法”,即将多分类任务拆为若干个二分类任务求解.具体来说,先对问题进行拆分,然后为拆出的每个二分类任务训练一个分类器;在测试时,对这些分类器的预测结果进行集成以获得最终的多分类结果。
最经典的拆分策略有三种:一对一(OvO),一对其余(OvR),多对多(MvM)。
OvR是每次将一个类的样例作为正例、所有其他类的样例作为反例来训练N 个分类器.在测试时若仅有一个分类器预测为正类,则对应的类别标记作为最终分类结果。
OvR 只需训练 N 个分类器,而 OvO 需训练 N (N - 1)/2 个分类器,因此, OvO 的存储开销和测试时间开销通常比 OvR 更大.
MvM 是绛次将若干个类作为正类,若干个其他类作为反类.显然, OvO 和OvR 是 MvM 的特例
. ECOC 工作过程主要分为两步:
• 编码:对 N 个类别做河次划分,每次划分将一部分类别划为正类,一部
分划为反类,从而形成一个二分类训练集;这样一共产生 M 个训练集,可
训练出 M 个分类器.
・解码: M 个分类器分别对测试样本进行预测,这些预测标记组成一个编
码.将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小
的类别作为最终预测结果.
1.6类别不平衡
如果是训练样例数产别很大,在学习的过程中会造成困扰,例如有 998 个反例,但正例只有 2个,那么学习方法只需返回一个永远将新样本预测为反例的学习器,就能达到 99.8% 的精度;然而这样的学习器往往没有价值,因为它不能预测出任何正例.
类别不平衡 (class-imbalance) 就是指分类任务中不同类别的训练样例数目差别很大的情况.不失一般性,本节假定正类样例较少,反类样例较多.在现实的分类学习任务中,我们经常会遇到类别不平衡,例如在通过拆分法解决多分类问题时,即使原始问题中不同类别的训练样例数目相当,在使用 OvR 、 MvM 策略后产生的二分类任务仍可能出现类别不平衡现象,因此有必要了解类别不平衡性处理的基本方法.
可以通过“再放缩”的策略去解决。
第一类是直接对训练集里的反类样例进行“欠采样” (undersampling), 即去除欠采样亦称“下采样”(downsampling), 过采样亦 称 "上 采 样 " (upsampling).一些反例使得正、反例数目接近,然后再进行学习;
第二类是对训练集里的正类样例进行“过采样" (oversampling), 即增加一些正例使得正、反例数目
接近,然后再进行学习;
第三类则是直接基于原始训练集进行学习;