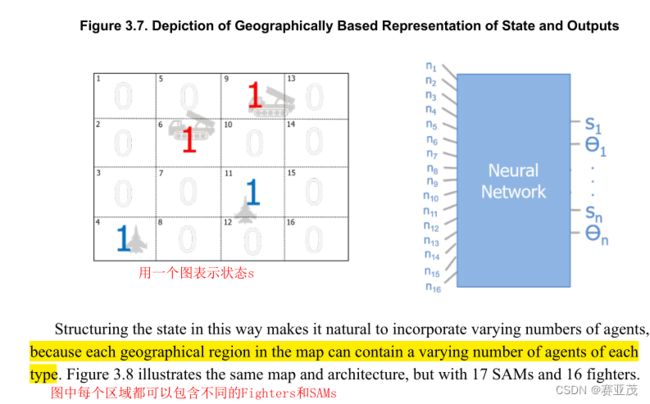
基于强化学习的多战机同SEAD联合作战空战辅助决策
1.带诱饵的战机打击策略
- 代码
环境的搭建部分的代码:
import numpy as np
import matplotlib.pyplot as plt
# 下面环境的搭建将是基于全局可观测的
# 下面写战斗机的类
class Fighter(object):
def __init__(self,x0=0.0,y0=0.0,fighter_range=20,
L_limits=100,velocity=2175.0/3600,
delta_t=10,aim_time=30):
# 下面设置战斗机的基本属性
self.x = x0
self.y = y0
self.fighter_range = fighter_range # 战斗机火力范围
self.L_limits = L_limits # 区域长度限制
self.velocity = velocity # 战斗机速度
self.delta_t = delta_t # 采样时间
self.aim_time = aim_time # 战斗机瞄准时间
self.dead = False # 战斗机的生存状态
self.state = np.array([self.x,self.y]) # 战斗机当前状态是包括x0,y0的np数组
# 下面建立离散动作空间的映射表
self.action2numbers = {'right':0,'right_up':1,'up':2,'left_up':3,'left':4,
'left_down':5,'down':6,'right_down':7,'wait':8}
self.action_space = ['right','right_up','up','left_up','left',
'left_down','down','right_down','wait']
# 下面开始设置瞄准时间
self.aim_SAM_time = 0.0
self.aim_target_time = 0.0
def reset(self,rand_initial_position=True):
# 试探性出发假设
if rand_initial_position:
self.x = np.random.random()*self.L_limits
self.y = np.random.random()*self.L_limits
else:
self.x = 0
self.y = 0
self.dead = False
# 下面开始设置瞄准时间
self.aim_SAM_time = 0.0
self.aim_target_time = 0.0
return np.array([self.x,self.y])
def step(self,action,SAM,target):
# 动作空间action表示航向{0,1,2,3,4,5,6,7}
# 这里需要知道SAM的实际位置与target的实际位置
# 下面开始获取当前战斗机位置
# SAM_range:SAM的火力范围
# 下面开始抽取target与SAM的状态
# 下面对动作进行描述
action_str = self.action_space[action]
if action_str == 'right': #如果战斗机往右跑
self.x += self.velocity*self.delta_t
self.y = self.y
elif action_str == 'right_up':
self.x += self.velocity*self.delta_t/np.sqrt(2)
self.y += self.velocity*self.delta_t/np.sqrt(2)
elif action_str == 'up':
self.x = self.x
self.y += self.velocity*self.delta_t
elif action_str == 'left_up':
self.x = self.x - self.velocity*self.delta_t/np.sqrt(2)
self.y += self.velocity*self.delta_t/np.sqrt(2)
elif action_str == 'left':
self.x = self.x - self.velocity*self.delta_t
self.y = self.y
elif action_str == 'left_down':
self.x = self.x - self.velocity*self.delta_t/np.sqrt(2)
self.y = self.y - self.velocity*self.delta_t/np.sqrt(2)
elif action_str == 'down':
self.x = self.x
self.y = self.y - self.velocity*self.delta_t
elif action_str == 'right_down':
self.x = self.x + self.velocity*self.delta_t/np.sqrt(2)
self.y = self.y - self.velocity*self.delta_t/np.sqrt(2)
else:
# 下面表示在原地等待
self.x = self.x
self.y = self.y
# 使战斗机位置在所在区域内
if self.x >= self.L_limits:
self.x = self.L_limits
elif self.x <= 0.0:
self.x = 0.0
if self.y >= self.L_limits:
self.y = self.L_limits
elif self.y <= 0.0:
self.y = 0.0
self.state = np.array([self.x,self.y])
# 下面开始计算奖励
d_target = np.linalg.norm(np.array([self.x - target.x,self.y - target.y]))
d_SAM = np.linalg.norm(np.array([self.x - SAM.x,self.y - SAM.y]))
# 如果SAM与target在战斗机的火力射程范围外,则无法瞄准,其瞄准时间为0
if d_target >= self.fighter_range:
self.aim_target_time = 0.0
else:
self.aim_target_time += self.delta_t
if d_SAM >= self.fighter_range:
self.aim_SAM_time = 0.0
else:
self.aim_SAM_time += self.delta_t
if d_SAM >= SAM.SAM_range: # Fighter在SAM的火力范围内会计算时间
SAM.aim_Fighter_time = 0.0
else:
SAM.aim_Fighter_time += self.delta_t
# 如果战斗机瞄准时间比较长可以击落target
if self.aim_target_time >= self.aim_time:
target.dead = True
self.aim_target_time = 0.0
return self.state,1000,True # 比较圆满的结果是target被击落
# 如果SAM有弹药且成功击毁Fighter
if (SAM.dead==False) and (d_SAM <= SAM.SAM_range) and (SAM.aim_Fighter_time >= SAM.aim_time):
SAM.dead = True # 此时弹药已经消耗光
SAM.aim_Fighter_time = 0.0
return self.state,-1000,True # 不太圆满的结果是Fighter被击落
# 战斗机同样也击落SAM的可能性
if (SAM.dead==False) and (d_SAM <= self.fighter_range) and (self.aim_SAM_time >= self.aim_time):
SAM.dead = True # SAM 被击毁
self.aim_SAM_time = 0.0
return self.state,50,False
return self.state,-1,False
# 下面开始写SAM的类
class Sam:
def __init__(self,x=50,y=50,SAM_range=30,
L_limits=100,max_aim_time=10):
self.x = x
self.y = y
self.SAM_range = SAM_range
self.L_limits = L_limits
self.aim_time = max_aim_time
self.aim_Fighter_time = 0
self.dead = False
def reset(self):
self.aim_Fighter_time = 0
self.dead = False
# 下面开始写target的类
class Target:
def __init__(self,x=80,y=80,L_limits=100):
self.x = x
self.y = y
self.L_limits = L_limits
self.dead = False
def reset(self):
self.dead = False
# 总环境的搭建
class Fighter2Env(object):
def __init__(self,SAM_x=50,SAM_y=50,Target_x=80,
Target_y=80,Fighter_range=20,SAM_range=30,
L_limits=100,delta_t=10,velocity=2175.0/3600,
fighter_aim_time=30,sam_aim_time=10):
# 构造两个同构战斗机
self.fighter1 = Fighter(x0=0,y0=0,fighter_range=Fighter_range,
L_limits=L_limits,velocity=velocity,
delta_t=delta_t,aim_time=fighter_aim_time)
self.fighter2 = Fighter(x0=0,y0=0,fighter_range=Fighter_range,
L_limits=L_limits,velocity=velocity,
delta_t=delta_t,aim_time=fighter_aim_time)
# 分别构造SAM与Target对象
self.Target = Target(x=Target_x,y=Target_y,L_limits=L_limits)
self.SAM = Sam(x=SAM_x,y=SAM_y,SAM_range=SAM_range,
L_limits=L_limits,max_aim_time=sam_aim_time)
self.observation_space = np.array([[0,L_limits],[0,L_limits],[0,L_limits],[0,L_limits]]) # 战斗机1,2的位置组成战斗机的状态空间
# self.action_space = [self.fighter1.action_space,self.fighter2.action_space]
self.action_space = [[0,1,2,3,4,5,6,7,8],[0,1,2,3,4,5,6,7,8]]
self.observation_ndim = 4
self.fighter1_action_dim = 9
self.action_dim = 81 # 9 * 9=81维动作空间,动作空间巨大是一个很大的问题
# 设置2架战斗机的初始位置
fighter1_x0,fighter1_y0 = self.fighter1.reset(rand_initial_position=True)
fighter2_x0,fighter2_y0 = self.fighter2.reset(rand_initial_position=True)
self.state = np.array([fighter1_x0,fighter1_y0,fighter2_x0,fighter2_y0])
self.fighter1_state = np.array([fighter1_x0,fighter1_y0])
self.fighter1_done = False # 这里说明两个战斗机都没有被击落
self.fighter1_total_rewards = 0
self.fighter1_x_array = []
self.fighter1_y_array = []
self.fighter2_state = np.array([fighter2_x0,fighter2_y0])
self.fighter2_done = False # 这里说明两个战斗机都没有被击落
self.fighter2_total_rewards = 0
self.fighter2_x_array = []
self.fighter2_y_array = []
self.done = False
# 下面是动作解码
def action_decode(self,action):
# action:0-80
fighter1_action = int(action)//self.fighter1_action_dim
fighter2_action = int(action)%self.fighter1_action_dim
return fighter1_action,fighter2_action
# 下面是重置函数
def reset(self,rand_initial_position=True):
# 设置2架战斗机的初始位置
fighter1_x0, fighter1_y0 = self.fighter1.reset(rand_initial_position=rand_initial_position)
fighter2_x0, fighter2_y0 = self.fighter2.reset(rand_initial_position=rand_initial_position)
self.state = np.array([fighter1_x0, fighter1_y0, fighter2_x0, fighter2_y0])
self.fighter1_state = np.array([fighter1_x0, fighter1_y0])
self.fighter1_done = False # 这里说明两个战斗机都没有被击落
self.fighter1_total_rewards = 0
self.fighter1_x_array = []
self.fighter1_y_array = []
self.fighter2_state = np.array([fighter2_x0, fighter2_y0])
self.fighter2_done = False # 这里说明两个战斗机都没有被击落
self.fighter2_total_rewards = 0
self.fighter2_x_array = []
self.fighter2_y_array = []
self.done = False # 回合结束标志
return self.state
# 下面是动作函数
def step(self,action):
# action:0-80
fighter1_action,fighter2_action = self.action_decode(action)
fighter1_total_rewards,fighter2_total_rewards = self.fighter1_total_rewards,self.fighter2_total_rewards
if not self.fighter1_done:
fighter1_state,fighter1_reward,fighter1_done = self.fighter1.step(fighter1_action,self.SAM,self.Target)
self.fighter1_x_array.append(fighter1_state[0])
self.fighter1_y_array.append(fighter1_state[1])
self.fighter1_done = fighter1_done
self.fighter1_state = fighter1_state
self.fighter1_total_rewards += fighter1_reward
if not self.fighter2_done:
fighter2_state,fighter2_reward,fighter2_done = self.fighter2.step(fighter2_action,self.SAM,self.Target)
self.fighter2_x_array.append(fighter2_state[0])
self.fighter2_y_array.append(fighter2_state[1])
self.fighter2_done = fighter2_done
self.fighter2_state = fighter2_state
self.fighter2_total_rewards += fighter2_reward
self.state = np.array([self.fighter1_state[0],self.fighter1_state[1],self.fighter2_state[0],self.fighter2_state[1]])
# 下面开始设置奖励函数
## 如果两个累计奖励都不变化
if (self.fighter1_total_rewards != fighter1_total_rewards) and (self.fighter2_total_rewards != fighter2_total_rewards):
reward = max(self.fighter1_total_rewards - fighter1_total_rewards,self.fighter2_total_rewards - fighter2_total_rewards)
else:
reward = (self.fighter1_total_rewards + self.fighter2_total_rewards) - (fighter1_total_rewards + fighter2_total_rewards)
# 当二者都True结束时真的结束
if self.fighter1_done and self.fighter2_done: # 这里可以用故障树分析!!!
self.done = True
else:
self.done = False
return self.state,reward,self.done
# 下面是根据画图
def render(self):
x1, y1 = [], []
for theta in np.linspace(-np.pi, np.pi):
x1.append(self.SAM.x + self.SAM.SAM_range * np.cos(theta))
y1.append(self.SAM.y + self.SAM.SAM_range * np.sin(theta))
plt.plot(self.fighter1_x_array,self.fighter1_y_array)
plt.plot(self.fighter2_x_array,self.fighter2_y_array)
plt.plot(x1,y1,'g.-')
plt.plot(self.SAM.x,self.SAM.y,'ro')
plt.plot(self.Target.x,self.Target.y,'b*')
plt.title("rewards1:{},rewards2:{}".format(self.fighter1_total_rewards,self.fighter2_total_rewards))
plt.legend(['Fighter1', 'Fighter2'])
plt.show()
用以下代码进行测试:
# 定义两个战斗机,target,以及SAM
limits = 100
delta_t = 10
env = Fighter2Env(delta_t=10,L_limits=limits,Fighter_range=10)
env.reset(rand_initial_position=False)
while True:
action = np.random.randint(low=0,high=81)
env.step(action)
if env.done:
break
env.render()
得到一组随机游走的测试结果为:
![]()
用PPO进行训练:
import matplotlib.pyplot as plt
from ppo_code import PPO
from fighter2 import Fighter2Env
# 下面是定义环境
env = Fighter2Env(delta_t=10,L_limits=100,Fighter_range=10,
SAM_range=30,SAM_x=50,SAM_y=50,Target_x=65,
Target_y=65,sam_aim_time=10,fighter_aim_time=20)
# 下面是定义参数阶段
ppo_net = PPO(num_inputs=4,num_outputs=81,num_hiddens=128,lr=0.001)
epsiode_rewards,mean_rewards = ppo_net.train_network(env,epsiodes=300)
# 下面开始画图
plt.plot(epsiode_rewards)
plt.plot(mean_rewards)
plt.xlabel('epsiode')
plt.ylabel('rewards')
plt.title(str(epsiode_rewards[-1]))
state = env.reset(rand_initial_position=False)
epsiode_reward = 0
fighter1_x,fighter1_y,fighter2_x,fighter2_y = [state[0]],[state[1]],[state[2]],[state[3]]
while True:
action,_ = ppo_net.policy.select_action(state)
next_state,reward,done = env.step(action)
fighter1_x.append(next_state[0])
fighter1_y.append(next_state[1])
fighter2_x.append(next_state[2])
fighter2_y.append(next_state[3])
epsiode_reward += reward
state = next_state
if done:
break
x1, y1 = [], []
for theta in np.linspace(-np.pi, np.pi):
x1.append(env.SAM.x + env.SAM.SAM_range * np.cos(theta))
y1.append(env.SAM.y + env.SAM.SAM_range * np.sin(theta))
plt.plot(fighter1_x,fighter1_y)
plt.plot(fighter2_x,fighter2_y)
plt.plot(x1,y1,'g.-')
plt.plot(env.SAM.x,env.SAM.y,'ro')
plt.plot(env.Target.x,env.Target.y,'b*')
plt.title("rewards1:{},rewards2:{}".format(env.fighter1_total_rewards,env.fighter2_total_rewards))
plt.legend(['Fighter1', 'Fighter2'])
plt.show()
2.拓展
3.附录
离散PPO代码:
import torch
import numpy as np
import torch.nn as nn
from torch.distributions import Categorical
# 下面将定义一个演员价值类
class ActorCritic(nn.Module):
def __init__(self,num_states,num_actions,num_hiddens=64,lr=0.01):
super(ActorCritic,self).__init__()
self.action_layers = nn.Sequential(
nn.Linear(num_states,num_hiddens),
nn.Tanh(),
nn.Linear(num_hiddens,num_actions),
nn.Tanh(),
nn.Softmax()
)
self.value_layers = nn.Sequential(
nn.Linear(num_states,num_hiddens),
nn.Tanh(),
nn.Linear(num_hiddens,1)
)
self.optimizer = torch.optim.Adam(self.parameters(),lr=lr)
def forward(self,state):
# 输入的state是numpy类型
pass
def select_action(self,state):
# 输入state是numpy类型
state = torch.from_numpy(state).float()
dist = self.action_layers(state)
#values = self.value_layers(state)
categorical = Categorical(dist)
action = categorical.sample()
log_prob = categorical.log_prob(action)
return action.item(),log_prob
# 评估lnpi(a|s),v(s)
def evaluate_action(self,state,action):
# 其中state是torch类型
# action是int类型
#state = torch.from_numpy(state).float()
# action = torch.tensor(action)
dist = self.action_layers(state)
values = self.value_layers(state)
action_probs = Categorical(dist).log_prob(action)
return action_probs,torch.squeeze(values)
# 下面将定义PPO算法的框架
class PPO(object):
def __init__(self,num_inputs=2,num_outputs=3,num_hiddens=64,epsilon=0.2,gamma=0.9,K_epochs=4,lr=0.01):
# 存储参数
self.gamma = gamma
self.epsilon = epsilon
# 定义一个老的参数policy网络与一个新的policy网络
self.policy = ActorCritic(num_states=num_inputs,num_actions=num_outputs,num_hiddens=num_hiddens,lr=lr)
self.policy_old = ActorCritic(num_states=num_inputs,num_actions=num_outputs,num_hiddens=num_hiddens,lr=lr)
self.policy_old.load_state_dict(self.policy.state_dict()) # 将theta_old 的初值考虑为与theta一样
# 误差项
self.mesLoss = nn.MSELoss()
self.k_epochs = K_epochs
self.optimizer = torch.optim.Adam(self.policy.parameters(),lr=lr)
self.losses = []
# 下面定义储存状态的数组
self.saved_states = []
self.saved_rewards = []
self.saved_log_probs = []
# self.saved_state_values = []
self.saved_actions = []
self.saved_is_done = []
# 策略更新(实际上是在更新网络参数)
def update_policy(self):
# 由存储的数组中的数据计算Gt(累计折扣回报)
discounted_rewards = []
G = 0
for reward,is_done in zip(reversed(self.saved_rewards),reversed(self.saved_is_done)):
if is_done:
G = 0
G = reward + G*self.gamma
discounted_rewards.insert(0,G)
# 折扣回报标准化
discounted_rewards = torch.tensor(discounted_rewards)
discounted_rewards = (discounted_rewards - torch.mean(discounted_rewards))/torch.std(discounted_rewards)
## 下面明天继续写先打骑砍了....
old_states = torch.tensor(self.saved_states).float()
old_actions = torch.tensor(self.saved_actions)
old_logprobs = torch.tensor(self.saved_log_probs)
# 优化策略
for _ in range(self.k_epochs):
logprobs,state_values = self.policy.evaluate_action(old_states,old_actions) #返回的应该是一个数组
#找到比率
ratio = torch.exp(logprobs - old_logprobs)
# 计算优势函数
advatange = discounted_rewards - state_values
surr1 = ratio*advatange
surr2 = torch.clamp(ratio,1-self.epsilon,1+self.epsilon)*advatange
loss = -torch.min(surr1,surr2) + 0.5*self.mesLoss(state_values,discounted_rewards)
self.losses.append(loss.mean()) # 用大数定理,均值逼近期望
# 采取梯度措施
self.optimizer.zero_grad()
loss.mean().backward()
self.optimizer.step()
# 将新的参数赋值到原来的网络theta_old中
self.policy_old.load_state_dict(self.policy.state_dict())
# 训练网络
def train_network(self,env,epsiodes=100):
epsiode_rewards = []
mean_rewards = []
for epsiode in range(epsiodes):
state = env.reset()
epsiode_reward = 0
while True:
action,log_prob = self.policy_old.select_action(state)
next_state,reward,done = env.step(action)
# 保存各个回报与参数
self.saved_log_probs.append(log_prob)
self.saved_states.append(state)
self.saved_actions.append(action)
self.saved_rewards.append(reward)
self.saved_is_done.append(done)
epsiode_reward += reward
# 状态转换
state = next_state
if done:
# 因为是MonteCarlo估计则每个轨迹结束后更新策略
self.update_policy()
self.clean()
break
epsiode_rewards.append(epsiode_reward)
mean_rewards.append(np.mean(epsiode_rewards[-10:]))
print("第{}回合的奖励值是{:.2f},平均奖励是{:.2f}".format(epsiode,epsiode_reward,mean_rewards[-1]))
return epsiode_rewards,mean_rewards
# 清空数组
def clean(self):
del self.saved_states[:]
del self.saved_actions[:]
del self.saved_rewards[:]
del self.saved_log_probs[:]
del self.saved_is_done[:]