gradient descent

learning rate  set the learning rate η carefully

adaptive learning rates

Reduce the learning rate by some factor every few epochs. 

learning rate随参数的update越来越小：刚开始里最低点比较远，故learning rate 可以调大一点，走快一点，但是当参数update几次之后比较靠近目标了就应当减小learning rate，使其能够收敛在目标附近

 Learning rate cannot be one-size-fits-all

        Giving different parameters different learning rates

                Adagrad: Divide the learning rate of each paremeter by the root mean square of its                                 previous derivatives每个参数的learning rate都除上过去所有微分值的root                                 mean square（均方根） 解决不同参数应该使用不同的更新速率问题，随着                                    算法不断迭代，累积平方梯度会越来越大，整体的学习率会越来越小

 

     

adagrad  gradient越大则分母越大，分子也越大，步长变化不确定

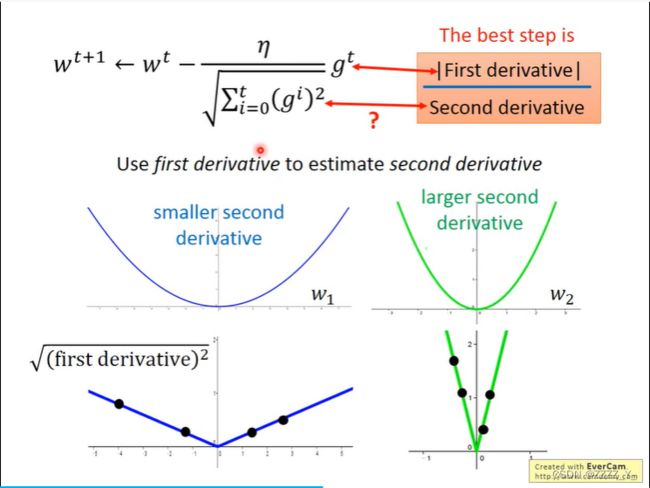
to show how surprise it is（反差）

只考虑一个参数时，微分值越大则离目标越远

而多个参数同时考虑时结论不成立，如上右图，比较a，c，a处的微分值小于c，但c离目标点更近。需要考虑二阶微分，蓝色曲线更平缓，a处的二阶微分值较小，而绿色曲线更陡峭，c处的二阶微分值较大，应将| 一阶微分值 | / 二阶微分值作为标准进行衡量

在平滑曲线的一阶微分图像中取多个sample点，其值普遍较小；而在陡峭尖锐曲线的一阶微分图像中取多个sample点，其值相对普遍较大 取sample点求均方根：过去所有微分平方

Adgrad计算σ时每个gradient都有同等的重要性，但是在RMSProp中可以自己调整现在的gradient有多重要，如下图所示，α越小表明现在算出来的gradient越重要

RMSProp

 

 上图情况下，当从平缓的地方到梯度较大地方时，若使用adagrad的话，它的反应比较慢，可能来不及调整，最终由于learning rate过大导致飞出去，但是若使用RMSProp的话，将α设置的小一点，这意味着新的gradient比较重要，那么就能很快的调整learning rate，减小步长，顺利刹车。当又走到较为平缓的地方时，gradient变小，若α较小，那么σ反应很快，它的值很快就变小了，那么步长就变大了

 Adam：RMSProp + Momentum

继续回来看adagrad

 首先，在到了拐点后，使用adagrad可以继续向左走，因为左右方向的gradient很小，那么步长就会自动调大，就能够很快前进。可后面还是出现了问题，在接近目标点时轨迹在纵轴方向上很不稳定，因为在一直左走的过程中，竖直方向的梯度一直都很小，很多个梯度累加起来后得到的σ也很小，那么就导致step很大，于是就飞出去了，飞出去后竖直方向的gradient很大，因此步长很快又会减小回来，因此可以看见飞出去后又会回来，如此来回往复。

如何解决呢？Learning Rate Decay:调整η是其为一个与时间有关的参数，如下图所示。

随着时间不断地进行η会不断的减小，因为随着时间的进行，我们离目标也不断接近，因此learning rate也需要减小，这是我们可以通过减小η实现

 通过这种方式，上面的问题就能得到解决

还有一种方式：Warm Up 

因为σ是通过统计数据得到的，数据量比较大的时候才比较可靠，当数据量太小的时候也就是在初始的时候，我们希望它的learning rate比较小，让他自己慢慢探索，当收集的数据变多了再慢慢增大learning rate

总结 some improvements

 

m和σ都用的之前所有的gradient，但二者还是不一样的，m是各个gradient的加和，既有梯度的方向信息又有大小信息 ，而σ只记录了gradient的大小信息

Stochastic Gradient Descent（随机梯度下降）

 每取一个example就update一次参数，

（？？？）

Feature Scaling

若不同feature的取值范围相差较大，则将数据做scaling，让不同的feature的scale相近，否则scale大的feature对应的权重较小，权重的变化对最终结果的影响会比较大，eg.   若x2的scale普遍较大，则w2值较小，w2的微小变化将导致y发生较大变化，y的值受w2的影响将较大，如下左图。

由上左图知，改变w2对loss影响较大，故w2方向上变化较快，w1方向上变化较慢，最终所成loss图像为椭圆，实际进行gradient decent时不同的方向需要不同的learning rate，而若feature进行了scale后所成图像为圆。前者update是沿着等高线的方向变化的，而后者是朝着最低点的方向变化的，因为等高线的方向就是朝着最低点的。

那么如何对feature做scaling呢

假设有一系列样本，每个样本有n个特征  设所有样本的第i个特征的mean均值为，standard deviation标准差为，则 为标准化的结果，均值为0，方差为1.

Question

when solving：  by gradient descent, each time we update the paremeters, we obtain θ that makes L(θ) smaller.     right or wrong?

wrong. learning rate调的太大可能会出现这种问题

由上图，右边低，前面低，故往右前方前进，即到箭头所指台阶处，最终高度反而变高

理论基础

如何找到最低点（目标点）？

以起始点为圆心画一个圈，找出圈内离最低点最近的点，然后再以该点为圆心画圈，进行更新，如此下去直到找到目标点，but怎么快速的在圈内找到离最低点最近的点呢。

先看泰勒公式，任何一个function h(x)，若在x=x0处无穷次可微，则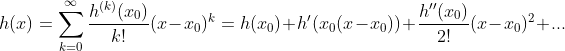

当x接近于x0时即，高阶项为无穷小，可忽略，

多元泰勒公式：

若圆圈很小，那么在这个范围内function loss可用泰勒公式简化，

令，则

需满足 

其中s，u，v，为constant，也就是要在圈内找到使loss最小的θ1和θ2

令，则

可视为两个向量 的外积，如下图所示

若要使乘积最小，则取的方向与相反，模长为最大，即为圆半径d，如下图所示

即  

带入得 

前提：圆圈足够小，即learning rate要足够小，否则结论不成立

按理说也能考虑二次项，理论上若考虑二次项/更高次项learning rate可以设置的更大些，但实际若考虑进来（如牛顿法）会导致计算量增大，计算效率变低，所以说主要还是用gradient 

Limitation of Gradient Descent ：

理论上：local minima，saddle point 

实际上：plateau，实际操作中会取到微分值小于10e-6时停下来，并非梯度值为0处，故可能会停在高原地方，不能确保是否离目标点很近