MATLAB学习笔记--插值和拟合

以下是我的关于插值和拟合的学习笔记，基本是根据课程内容写的，有一些例题源自网络。第一次写，肯定有很多不足，希望多多包涵啦

(一）插值与拟合

插值

在平面上给出一组离散点列，要求一条曲线，把这些点按次序来凝结起来，称为插值。

拟合

拟合就是利用平面上一系列的点，寻找f(x)，使得f(x)在某种准则下与所有的点最接近。

插值与拟合的比较

一.相同点
都属于函数逼近的方法
都能进行数据估计
二.不同点
（1） 实现方法不同 ：拟合是已知点列，从整体上靠近它们；插值是已知点列并且完全经过点列。
（2）在图像上是不同:图像中的插值必须通过数据，图像中的拟合必须得到最接近的结果，这取决于整体效果。
（3）在几何意义上不同：拟合就是寻找一个具有已知形状和未知参数的连续曲面来最大程度地逼近这些点，而插值就是找到一个连续的曲面（或几个分段光滑曲面）通过这些点。
（4）应用不同：当不要求逼近函数在已知数据点与被逼近函数完全一致时，而仅是尽量接近这些点时可以采用拟合。同理，若要求严格，则只能选用插值

(二）一维插值及MATLAB实现

插值问题的主要任务：利用已知点构造一个简单的f(x),满足f(xi)=yi,再利用这个函数求出f(x0),其中f(x)称为插值函数，x0称为插值节点。

一维插值方法

一.拉格朗日插值
已知函数f(x)在n+1个点x0,x1,…,xn处的函数值为y0,y1,…,yn。求一n次多项式函数Pn(x)，使其满足Pn(xi)=yi,i=0,1,…,n.
公式
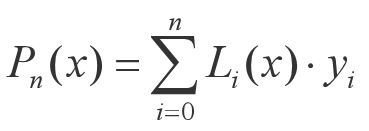其中

两点一次(线性)多项式
三点两次(抛物)插值多项式：总结：当拉格朗日插值在使用时，节点个数很多，即进行高次插值时会出现误差反而增大的现象——龙格现象。由此可见，由于拉格朗日插值的不稳定性，我们利用积分思想提出了另一种插值方法——分段插值法

二.分段插值
1.基本原理：将每两个相邻的节点用直线连起来，如此形成的一条折线就是分段线性插值函数。计算点的插值时，只用到左右的两个节点，计算量与节点个数n（初始值x0，y0的长度,n=length(x0)）无关，而拉格朗日插值与n值有关。分段线性插值中n越大，分段越多，插值误差越小。
1.公式：
总结：优点：相当于在每一个小区间上进行一次拉格朗日插值，计算量小，并且分段越多，计算的误差越小。
缺点：分段插值的分段点不光滑

由分段插值的缺点可知，在做插值时需要考虑分段点的光滑性，即要从导数的角度考虑。在此问题上，我们想出了一种解决方法——三次样条插值
三.三次样条插值
定义：x0,x1…xn为区间[a,b]的一个划分，如果函数S(x)在区间[a,b]上满足条件：
(1)S(x)在每个小区间[Xi-1,Xi]上都是三次多项式
(2)S(x),S’(x),S’’(x)都在区间[a,b]上连续
称S(x)为区间[a,b]上的三次样条函数，如果函数f(x)在节点x0,x1…xn处的函数值为f(xi)=yi,i=1,2…n.而三次样条函数S(x)满足S(xi)=yi,i=1,2…n.则称S(x)为f(x)在[a,b]上的三次样条插值函数

一维插值方法的MATLAB实现

一.
yi = interp1(x,y,xi,method)
其中，x、y为已知的数据点，xi为想要插值数据点的横坐标，返回对应的纵坐标yi。method为插值方法。
method:
nearest
最近邻点插值，即若xixi x_ixi​离xx xx最近，则yi=yyi=y y_i=yyi​=y
linear
线性插值，即插值的结果是一条条线段。
spline
进行三次样条插值，所得图形为光滑曲线，并且是二阶光滑的。
二.
在MATLAB中使用interp1的各类方法并进行比较
以下代码由于我还不会使用代码片，所以直接截图
运行结果如下：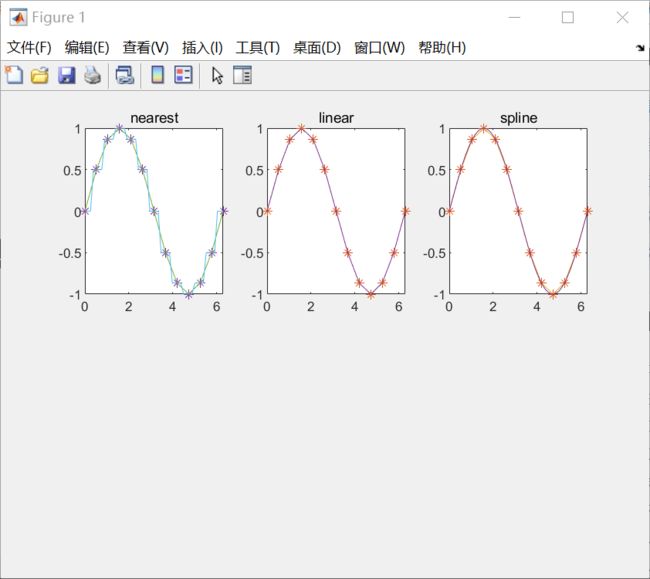
由图可知：最邻近点插值误差较大。分段线性插值结果最好，误差最小。三次样条插值有一点误差，但不是很大，并且得到的曲线比较光滑。

说明：由于MATLAB不提供拉格朗日插值函数，需要自己写，这里就不给出进一步的使用。

(三）二维插值及MATLAB实现

二维插值方法

1.基本思想：根据已知数据点(xi,yi,zi)，构造一个具有一定光滑性简单易于计算的函数z=f(x,y)(已知曲面)，作为z=g(x,y)(未知曲面）的近似，使曲线z=f(x,y)通过已知数据点，即f(xi,yj)=zij.然后计算点(x,y)的函数值f(x,y)作为g(x,y)的近似值。
2.两种情况
a.网格节点插值法：
最邻近点插值。 缺点：不连续
分片线性插值
分片双线性插值
分片双三次样条插值

b.散乱节点插值法：
修正Shephard法

二维插值方法的MATLAB实现

z = interp2(x0,y0,z0,x,y,method）
说明：其中，z是指被插值点的函数值，(x0,y0,z0)是指插值节点，(x,y)是指插值点，method是指插值方法
要求：x0,y0单调；x,y可以取为矩阵，或x取行向量，y取为列向量，x,y的值分别不能超出x0,y0的范围。
method:
最邻近的插值——nearest
双线性插值——linear
三次样条插值——spline
双三次插值——cubic
缺省值时，默认为双线性插值
z = griddata(x0,y0,z0,x,y,method)。对于散乱节点插值，课程中并未详细介绍，这里也不具体讲解

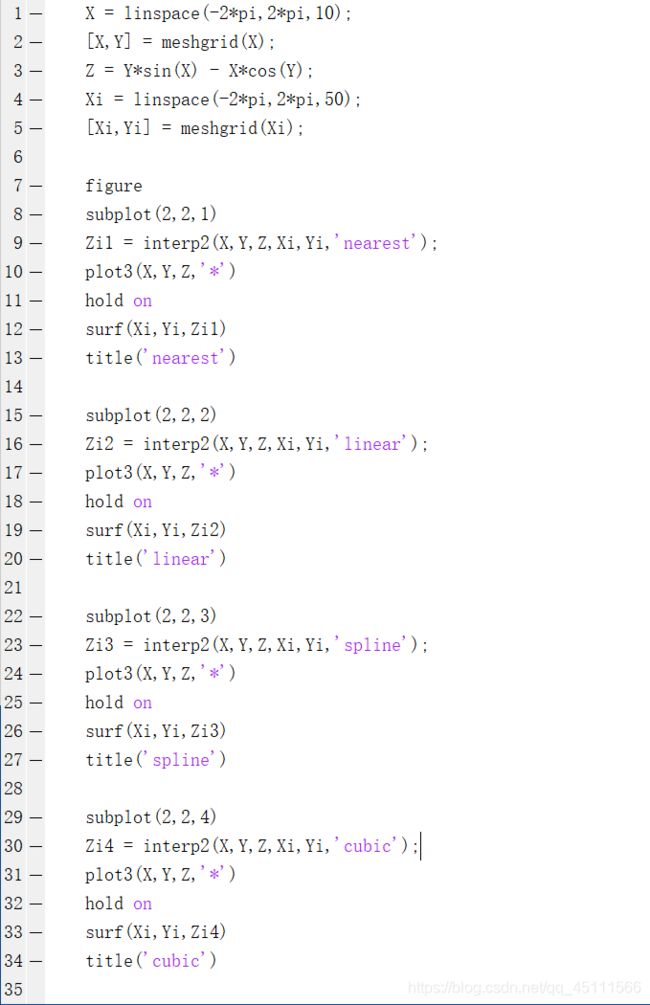
以上是interp2的几种二维插值方法的使用实例以及比较。（不会用代码片，所以截图啦）

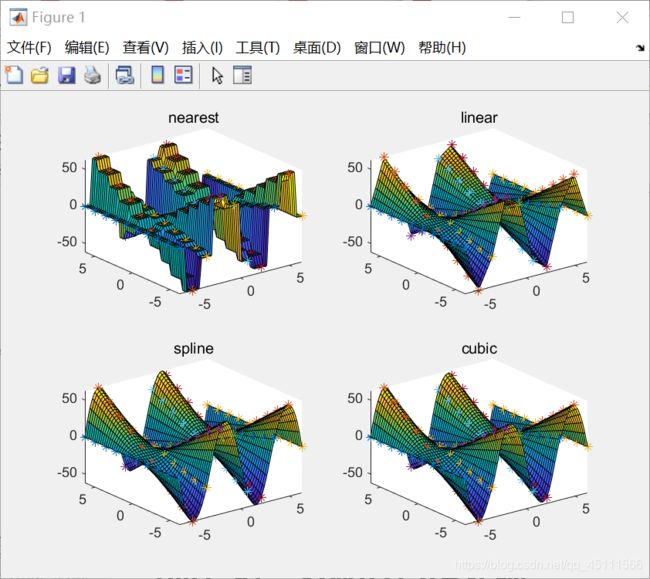
由结果可以看出，最临近点插值的缺点很明显（不连续），三次样条插值和双三次插值的图像更光滑。

其他插值命令
1.VI=interp3(X,Y,Z,V,XI,YI,ZI,method).很容易看出这就是三维插值的实现，这里的method方法与二维插值几乎是相同的
2.meshgrid：功能 生成用于画三维图形的矩阵数据,格式 [X,Y] = meshgrid(x,y) 将由向量x，y（可以是不同方向的）指定的区域[min(x)，max(x) ， min(y) ， max(y)] 用直线x=x(i),y=y(j) （ i=1,2,…,length(x) ，j=1,2,…,length(y)）进行划分。这样，得到了length(x)*length(y)个点
3.VI=interpn(x1,x2…xn,v,y1,y2…,yn,method).返回由参量X1,X2,…,Xn,V 确定的n 元函数V=V(X1,X2,…,Xn)在点（Y1,Y2,…,Yn）处的插值,参量Y1,Y2,…,Yn 是同型的矩阵或向量

(四）拟合及MATLAB实现

曲线拟合

1.与数据插值类似，曲线拟合也是一种函数逼近的方法。构造函数g(x)去逼近未知函数f(x)，使得误差g(xi)-f(xi)(i=1,2…n)在某中意义下达到最小。

2.曲线拟合思想：拟合就是把平面上一系列的点，寻找f(x)，使得f(x)在某种准则下与所有的最接近。

3.关键问题：
a.距离准则：因为涉及求导，采用欧式距离
b.拟合函数选择：
根据函数点的形态直接选择；
采用数学建模的方式，或者物理推导来确定函数形式；
实践过程中得出的经验公式
c.求解拟合函数

拟合的MATLAB实现

多项式拟合，如果取{r1(x),r2(x),rm+1(x)r1(x),r2(x),rm+1(x)}={1,x,…,xm1,x,…,xm}.即用m次多项式拟合给定数据，Matlab中有现成的函数p=polyfit(x0,y0,m)
说明：其中x,y为输入，表示同长度的数组；m表示拟合多项式的次数；a为一个数组，表示拟合多项式的系数
线性拟合实际上相当于多项式拟合时次数是1的情况
也即p=polyfit(t,X,1)

最小二乘拟合：
在Matlab中 使用polyfit()函数对数据进行最小二乘法拟合，调用格式：p = polyfit(x,y,n)
(1) 返回阶乘为n的多项式P(x)的系数.该阶乘是y中数据的最佳拟合(最小二乘法中)
(2) p 中的系数按降幂排列，p 的长度为 n+1 (p:向量)例如：x，y是给定的数据中的所有点的横坐标和纵坐标，n为要拟合的线性的幂。
(3) p = polyfit(x,y,2);
这里polyfit 即表示用一个最高次为 2次的多项式来拟合返回的p：计算出来的拟合曲线对应的幂的系数。 按照降幂排列。
例如：得到的 p 为：3 2 3
即对应的拟合曲线为：3x^2 + 2x + 3;

这里取n=1,使用最简单的线性拟合方式，结果如下图：

非线性最小二乘拟合
除了上面提到的最小二乘拟合多项式，当我们寻找函数f(x)是任意的非线性函数，则称为非线性最小二乘拟合.以下是它的MATLAB实现：
lsqnonlin
其最简单的调用格式为：

x=lsqnonlin(@F,x0, v1,v2)

其最复杂的调用格式为：

[x,norm,res,ef,out,lam,jac] = lsqnonlin(@F,x0,v1,v2,opt,P1,P2, … )

lsqcurvefit
其最简单的调用格式为：

x=lsqcurvefit(@F, x0,t,y,v1,v2)

其最复杂的调用格式为：

[x,norm,res,ef,out,lam,jac] = lsqcurvefit(@F,x0,t,y,v1,v2,opt,P1,P2,…)