特征工程

数据集成的含义是什么？数据集成的常用方法及含义是什么？

数据集成的含义

数据集成，就是将若干个分散的数据源中的数据（即不同来源、不同格式、不同特点的数据），通过某种方法（逻辑地或者物理地）将这些数据整合在一起。通过数据集成将数据整合在一起，用户能够通过数据集成系统访问数据。

数据集成的方法

1.联邦数据库

联邦数据库是一种模式集成方法，即通过消除各个数据源之间的异构性，各个数据库之间通过访问接口相互之间分享数据。异构数据的整合目标在于实现不同结构数据之间的数据信息、硬件设备资源和人力资源的合并和分享。

2.中间件集成

中间件位于应用层（应用程序）和数据层（异构数据源）之间，它向下协调各个数据源，向上为应用层提供数据访问的接口。用户通过用用层发起查询请求，中间件处理用户请求，将请求转换成各个数据源能够处理的子查询请求，然后发送给每个数据源的封装器，封装器与数据源交互，执行子查询请求，然后返回给中间件，中间件将结果返回给用户。

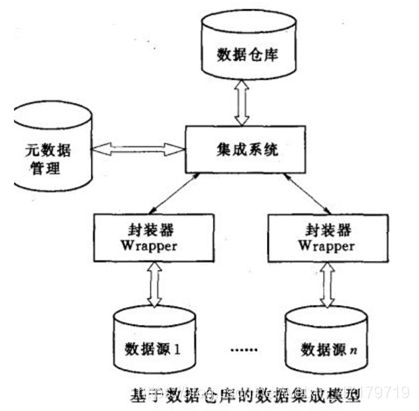
3.数据仓库

数据仓库是一种数据复制方法。此方法将各个数据源的数据复制数据仓库，用户直接访问数据仓库。

什么是数据的特征？特征工程的动机与目标是什么？

数据的特征

数据的特征是从数据中提取出来的对原始数据有用的信息，它能够区分与其他事物的属性，使得某数据区别于其他数据。

特征工程的动机与目标

特征工程是指把原始数据转换为模型的训练数据的过程。在机器学习中，特征工程就是把输入空间转换为特征空间的过程。 为了最大限度地从众多特征中选择尽可能相关的特征，以此来达到简化模型、降低计算复杂度、缩短模型的训练时间、避免过多的维度及降低过拟合等目的，使得提取的特征更好的适应模型。

特征选择的方法有哪些？它们的原理和实施步骤是什么？

如果数据的特征不发散，也就是说在这个特征上不同的样本之间没有差异，那么这个特征就不能很好的起到区分样本的作用。特征选择的一个原因来自于此。此外，我们总是想要找到和目标值（例如回归分析中的因变量$y$值）相关的特征，这个特征可以是正相关的，也可以是负相关的。如果这个特征和所要研究的问题没有多少关联，那就没有必要使用这个特征。特征选择就是从样本中选取重要的特征子集。

特征选择的方法

主要有：过滤法（Filter），包裹法（Wrapper），嵌入法（Embedded）

原理和步骤

1.过滤法

原理：根据发散性或者相关性，选择特征子集。

常用方法：方差法、相关性法、${\chi }^2$检验、F检验、互信息法

步骤：

a.按照发散性或相关性对各个特征评分

b.设定阈值

c.选择特征

比如说通过方差法计算各个特征的方差，每个特征都会对应一个方差，然后设定一个基础阈值，当该维度的特征方差小于基础阈值时，则丢弃该特征。

比如说相关性法：单变量特征选择能够对每一个特征进行测试，独立衡量该特征和响应变量之间的关系，根据得分扔掉不好的特征。如使用person、spearman相关系数；使用卡方检验对特征进行测试：卡方通常用于检验两个变量间的独立性，在做特征选择时我们希望检验每个特征和类别之间的独立性，对于每个特征我们假设特征和类别相互独立。卡方值越大越偏离于这个假设，说明特征和类别不相互独立是我们想要选择的特征，因此对卡方值从大到小进行排序，选择前$k$个。

2.包裹法

原理：选取提供特征重要性的算法，使用这些算法来进行特征选择。

常用方法：回归分析中的向前、向后、逐步回归；机器学习模型：随机森林（Random Forest）、梯度提升决策树（GBDT）、XGBoost、SVM等

步骤：

a.选择特定方法

b.训练模型，得到特征（或者特征评分）

b.选择特征

以随机森林为例：

比如说使用随机森林来进行特征的选择。随机森林能够计算单个特征变量的重要性。这一方法在很多地方得到应用，例如在信用评估领域，信用评估模型的数据特征有很多，其中不乏有很多噪音，所以需要计算出每一个特征的重要性并对这些特征进行一个排序，进而可以从所有特征中选择出重要性靠前的特征。

随机森林对某个特征的重要性计算原理如下：

对随机森林中的每一颗树，使用袋外数据$OOB$（称测试样本集中的观测为袋外观测，训练样本集中的观测为袋内观测）来计算这颗树的袋外误差$OOB{E}_i$，然后随机地对袋外数据$OOB$中的这个特征加入噪声干扰（就可以随机的改变样本在此特征处的值），再次计算袋外误差，记作$OOB{E}_i^{\prime }$，那么这个特征的特征重要性（variable importance，VI）定义如下：
$$VI=\frac{1}{n_{tree}}\sum _{i=1}^{n_{tree}}(OOB{E}_i^{\prime }-OOB{E}_i)$$
其中$n_{tree}$代表随机森林中树的个数。

使用这个式子来衡量特征重要性的原因是：若给某个特征随机加入噪声之后，袋外的准确率大幅度降低，则说明这个特征对于样本的分类结果影响很大，也就是说它的重要程度比较高。

计算了每个特征的重要性之后，从大到小进行排序。然后确定要删除的特征比例，从当前的特征变量中剔除相应比例不重要的指标，从而得到一个新的特征集。用新的特征集建立新的随机森林，并计算特征集中每个特征的$VI$值，并排序。

重复上述步骤，对每一次的特征集建立随机森林模型，然后计算对应的袋外误差，选择袋外误差最小的特征集作为最终的特征集。

3.嵌入法

**原理：**利用正则化的思想，在损失函数上再加入正则项，不断的利用梯度下降极小化损失函数，调整一些特征的权重，有些特征权重变为0，则舍弃这个特征，没被舍弃的特征就是被选择出来。

常用方法：L1正则

步骤：

a.拟合模型

b.计算损失函数

c.极小化损失函数，调整权重

d.特征选择

特征提取和特征选择的区别与联系

相同点

两者达到的效果是一样的，都是试图去减少特征数据集中的特征的数目

不同点

两者所采用的方式不同：

• 降维的方法主要是通过属性间的关系，如组合不同的属性得到新的属性，这样就改变了原来的特征空间
• 特征选择的方法是从原始特征数据集中选择出子集，是一种包含的关系，没有更改原始的特征空间。

特征生成的方法有哪些？它们的原理和实施步骤是什么？

特征生成是根据已有的特征，生成新的特征。

特征生成的一些方法

特征生成的方法主要有：时间截处理、分解类别属性、分箱、组合分类、特征缩放、特征提取、特征组合。

方法	说明
时间截处理	时间通常用年月日时分秒来表示，当在进行分析时，我们需要根据需求来选择需要的时间。时间截处理就是利用这个思想，例如需要月份，那么就可以只截取月份而舍弃年、日、时分秒。
分解类别属性	也称为独热（one-hot)。一些属性是类别型而不是数值型。例如，由{红，绿、蓝}组成的颜色属性，最常用的方式是把每个类别属性转换成二元属性，即从{0,1}取一个值。因此基本上增加的属性等于相应数目的类别，并且对于你数据集中的每个实例，只有一个是1（其他的为0）。
分箱	分箱是将数值型属性转换成类别型数据，即将一定范围内的数值划分成确定的块，使算法减少噪声的干扰。只有在了解属性的领域知识的基础上，确定属性能够划分成简洁的范围时分箱才有意义。
组合分类	组合分类是将两个或更多的类别属性组合成一个。当组合的特征要比单个特征更好时，这是一项非常有用的技术。假如有特征A、B , A有两个可能的取值{A1，A2}。B有两个可能的取值{B1，B2}。然后，A&B之间的组合特征如下：{（A1，B1），（A1，B2），（A2，B1），（A2，B2）}。可以给这些组合特征取任何名字，但是需要明白每个组合特征其实代表着A和B各自信息协同作用。（经度，纬度）就是组合分类的一个例子，一个相同的经度对应了地图上很多的地方，纬度也是一样。但是一旦你将经度和纬度组合到一起，它们就代表了地理上特定的一块区域，区域中每一部分是拥有着类似的特性。
特征缩放	一些特征比其他特征具有较大的跨度值。例如，将一个人的收入和他的年龄进行比较。数据的标准化就是特征缩放的一种方法，通过标准化将特征值缩放到相同的范围值内，可以避免某些特征比其他特征获得大小非常悬殊的权重值。
特征提取	特征提取涉及到从原始属性中自动生成一些新的特征集的一系列算法，降维算法就属于这一类。特征提取是一个自动将观测值降维到一个足够建模的小数据集的过程，常用的方法有主成分分析等。
特征组合	特征组合就是将不同的特征组合在一起，形成新的特征，这和组合分类不一样。特征组合主要有加法（几个特征相加）、乘法（几个特征相乘，如长乘宽得面积）、除法（几个特征相除，如房屋总价除以面积得每平米价格）

数据约简的目的是什么？数据约简的方法有哪些？他们的作用是什么？

目的

在数据集成与清洗后，我们能够得到整合了多个数据源且数据质量完好的数据集。但是，集成与清洗无法改变数据集的规模。所以需要降低数据规模，数据约简通过缩小数据分析和挖掘所需要的数据集规模，来减少数据分析和挖掘的时间。

方法

数据约简主要分为维度归约和数量归约。

1.维度归约

减少所考虑的随机变量或属性的个数。

特征生成：主成分分析

主成分分析通过寻找原自变量的正交向量，将原有的n个自变量重新组合为不相关的新自变量。当数据中存在的自变量个数过多，或者自变量之间存在相关性时，可以考虑使用PCA的方法重构自变量。

特征选择

特征选择通过删除不相关或冗余的属性来减少维度与数据量。其目的就是从全部特征中选取一个特征属性子集，使构造出来的模型更好。

一些其他的方法

如小波变换，通过傅里叶变换将信号分解成正余弦函数。在数据规约中，对数据进行小波转换后截断数据，保存最强的小波系数，从而保留近似的压缩数据。

2.数量归约

用替代的、较小的数据表示形式换原始数据。

参数化

使用模型估计数据，使得只需要存放模型参数而不存放实际数据。

非参数化

a.直方图

直方图方法相当于分箱处理，即将数据划分为不相交的子集，并且每个子集中的值对应一个相同的值。

b.聚类

通过聚类算法，将数据进行分群处理，用每个簇中的代表来代替实际的数据，从而实现数据的约简。

c.抽样

有时候数据的样本量会很大，如果将所有样本都用作分析会大大增加计算机的负担，甚至于有时候个人PC都不能够处理样本量巨大的数据集。抽样技术通过选则样本子集，用小样本代替大样本。抽样方法包括有简单随机抽样、分层随机抽样、整群抽样、多阶段抽样以及系统抽样。

数据变换的目标是什么？数据标准化的方法及特征是什么？偏态分布的处理方法及特征是什么？连续变量的离散化方法是什么？常用特征编码方法及适用范围？

目的

• 去除量纲

• 提高模型的解释性

  比如回归分析不处理的话，数据之间差距太大，如0.1与10000比较，那么建模出来的系数大小如何解释？所以需要进行数据标准化。

• 加快模型收敛速度

数据标准化的方法及特征

1. 中心化（z-score)

将数据映射为均值为0，方差为1的数据，如下所示：
$$x_i^{\prime }=\frac{x_i-\bar{x}}{s},i=1,2,...,n$$

2. 0-1标准化（最大最小法）

该方法将数据映射到区间$[0,1]$之间，如下所示：
$$x_i^{\prime }=\frac{x_i-min(x)}{max(x)-min(x)},i=1,2,...,n$$

3. 归一化

数据归一化，是将数据变为$(0,1)$之间的小数，如下所示：
$$x_i^{\prime }=\frac{x_i}{{\sum }_{k=1}^n{x}_k},i=1,2,...,n$$

4. 对数函数变换

对数据作对数变换后，不会改变数据的相对关系，对数函数变换如下：
$$x_i=\frac{log(x_i)}{log(max(x_i))}$$

5. 小数定标标准化

整体移动变量的小数点位置达到标准化，移动的最大位数取决于最大值，比如最大值为255，则移动三位：0.255

偏态分布的处理方法及特征

偏态分布是指频数分布不对称，数据的集中位置偏向一侧。如果频数分布的高峰向左偏移，长尾向右侧延伸称为右偏态分布；如果频数分布的高峰向右偏移，长尾向左延伸则成为左偏态分布。

如果数据是右偏的，可以取对数，或者取平方根，其原理是这样变化后导数随变量取值的增大而减小，也就是数据的增速放缓，就可以把大的数据向左移，使数据接近正态分布。如果数据是左偏的，可以通过取相反数的方法将数据转换为右偏的，然后再根据右偏的情况进行处理。

偏态分布中常用$Box-Cox$变换，其原理如下：
$$y^{(\lambda )}=\{\begin{array}{l}\frac{y^{\lambda }-1}{\lambda },\lambda \ne 0\\ log(y),\lambda =0\end{array}$$
其中$y$需要大于0，$\lambda$为待定的参数。

连续变量离散化

1.无监督离散化

• 等宽

  用等宽度区间进行划分数据

• 等频

  划分为$k$个区间，每个区间有相同数量的样本

• 聚类

  通过聚类的方法，对每一类进行统一标记。

2.有监督离散化

​ 如果数据在离散化的过程中使用到类标签信息，那么就是有监督离散化。

常用特征编码及适用范围

1. 分类

• 独热（one hot）

  一些属性是类别型而不是数值型，最常用的方式是把每个类别属性转换成二元属性，即从{0,1}取一个值。例如用(0,1)表示男性，(1,0)表示女性。

  使用范围：该方法适用于每个类别相互独立，且样本取值数量较少的情况，否则二进制向量的维度会急剧增加导致计算的困难。

• 标签

  对特征中的每个取值贴上标签，如用1来表示男性，用0来表示女性。

  适用范围：适用于分类数据，且对数值大小不敏感。

2. 连续

• 分箱

  在金融风控领域，通过分箱将连续型数值变量变为类别变量，然后通过$WOE$编码数据。如下所示：
  $$WO{E}_i=ln(\frac{p{y}_i}{p{n}_i})$$
  其中，$p{y}_i$表示第$i$个分箱中，响应数占所有样本响应数的比例；$p{n}_i$为表示$i$个分箱中，未响应数占所有样本中未响应数的比例。

  适用范围，分箱适用于连续型的数值型数据，且对数值的大小敏感。