SGAT: a Self-supervised Graph Attention Network for Biomedical Relation Extraction
论文地址:SGAT: a Self-supervised Graph Attention Network for Biomedical Relation Extraction
1. Introduction
近年来,在BioRE任务的研究中,提出了基于深度学习的不同方法。
目前,通过挖掘原始数据的特征构造辅助任务和伪标签的自监督学习方法已广泛应用于计算机视觉和自然语言处理领域。辅助任务可以指导原始模型捕获对主要任务更为关键的特殊特征。
受上述启发,我们通过将自我监督融入到图形注意机制中,构建了一个新的 BioRE 模型,称为 SGAT(self-survered graph attention network)。我们引入 GAT 的一个原因是:它在冗长复杂的生物医学文本中表现良好。
然而,如果没有任何指导,GAT 就无法有效地学习句法信息,甚至他们实际学习的内容都是未知的。直观地说,基于依赖关系的解析树的监督可以帮助学习特定的语法信息。为了缓解语法分析器生成的基于依赖关系的解析树通常很嘈杂的问题,我们在 SGAT 中使用了多头注意机制。我们只用基于依赖关系的解析树来监督一个头,其它的头仍然采用无监督来减少解析树噪声的影响。因此,我们提出的 SGAT 可以在基于依赖关系的解析树的监督下进行解释,并且尽可能少地受到噪声的影响。
与监督不同,自我监督只需要在语料库上添加少量注释,并利用原始数据的特性来构建伪标签。因此,我们使用基于依赖关系的解析树中的依赖关系作为标签,以指导模型更好地学习句法特征。
(1)我们通过每个句子的依赖关系解析树构造一个邻接矩阵,称为依赖矩阵。具体来说,如果两个单词之间存在依赖边,则它们在依赖矩阵中的值将设置为1,否则设置为0。
(2)有一些矩阵衡量多头 GAT 中单词间关系的重要性,我们选择其中一个作为注意矩阵。我们之所以选择其中一个是因为其它的头会关注其他的重要特征。
(3)我们计算并添加依赖矩阵和注意矩阵之间的损失,使注意矩阵尽可能与依赖矩阵相似,以便模型能够更好地学习句子的句法特征。
(4)使用工具对句子解析的结果有时不适合下游任务。为了解决这个问题,我们引入了 Gumbel Tree-GRU 。Gumbel Tree-GRU 基于贪心策略自动将单词表示转换为句子表示。
我们的贡献可以总结如下:
(1)提出了一种 SGAT,它在从复杂和嘈杂的双医学文本中提取生物医学关系方面具有优势。这是首次将自监督引入关系提取的图注意机制。
(2)引入 Gumbel Tree-GRU 来获得句子表示,这提高了模型对下游 BioRE 任务的适应性。
(3)在图注意机制中加入自监督可以有效地提高BioRE的性能。
2. Methodology
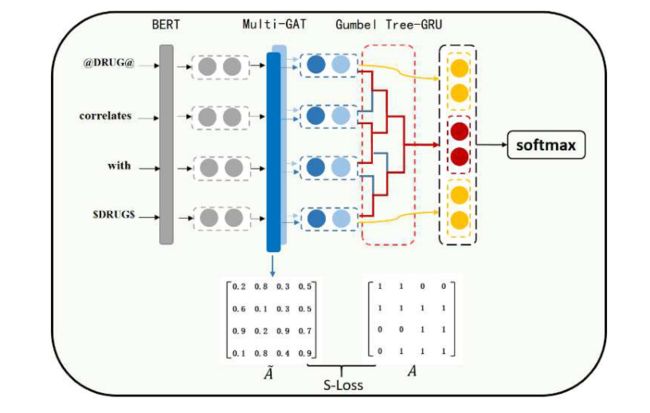
我们模型的总体架构包含四个模块:BERT表示层、自监督图注意层、Gumbel Tree-GRU层和知识融合层。
首先,用特殊符号替换实体,并从 BERT 中生成高质量的动态单词嵌入。然后将单词嵌入到自监督图形注意层中以提取语义和句法特征。接下来,自监督图注意层生成的隐藏单词特征通过 Gumbel Tree-GRU 层转换为句子特征。最后,我们融合两种实体特征和句子特征进行关系分类。
2.1 BERT 表示层
给定一个序列作为输入,BERT 使用 WordPiece 标记器来解决词汇表外的问题。例如,词汇表中未包含的“antiginatic”将被切成 {“antigator”,“##ic”}。为此,我们平均子标记的特征以获得完整的单词信息。
2.2 自监督图注意层
用工具解析的基于依赖关系的解析树通常与实际语法结构略有不同。因此,基于依赖关系的解析树生成的图形是有噪声的,这会导致 GCN 学习错误的知识。虽然 GATs 可以在一定程度上缓解这一问题,但它学习句法特征的能力有所下降。此外,对 GATs 实际学到的东西几乎没有了解。自监督图注意层不仅可以捕获更多的语法特征,而且可以减少基于依赖关系的解析树中噪声的影响。
(1)图注意机制
图注意机制通过全连通图传播信息,其中每个单词都被视为一个节点,节点间边的值由注意机制计算。在这项工作中,我们引入了多头自注意力机制。如果 X = [ x 1 , x 2 , ⋯ , x N ] X=[x_1,x_2,\cdots,x_N] X=[x1,x2,⋯,xN] 和 H = [ h 1 , h 2 , ⋯ , h N ] H=[h_1,h_2,\cdots,h_N] H=[h1,h2,⋯,hN] 分别表示输入特征和输出特征,传播可以公式化如下: A t = softmax ( W Q t X × ( W K t X ) T d k ) , t ∈ { 1 , 2 , ⋯ , N h } (1) A^t=\text{softmax}\Big(\frac{W_Q^tX\times(W_K^tX)^T}{\sqrt{d_k}}\Big),t\in\{1,2,\cdots,N_h\}\tag{1} At=softmax(dkWQtX×(WKtX)T),t∈{1,2,⋯,Nh}(1) h i t = f ( ∑ j = 1 N a i j t W t x j + b t ) , a i j t ∈ A t (2) h_i^t=f(\sum_{j=1}^Na_{ij}^tW^tx_j+b^t),a_{ij}^t\in A^t\tag{2} hit=f(j=1∑NaijtWtxj+bt),aijt∈At(2) h i = ∑ t = 1 N h h i t N h (3) h_i=\sum_{t=1}^{N_h}\frac{h_i^t}{N_h}\tag{3} hi=t=1∑NhNhhit(3)其中 N h N_h Nh 表示头数, A t ∈ R N × N A^t\in R^{N\times N} At∈RN×N 表示第 t t t 个头的注意矩阵, W Q t ∈ R d h × d k , W K t ∈ R d h × d k , W t ∈ R d h × d h W_Q^t\in R^{d_h\times d_k},W_K^t\in R^{d_h\times d_k},W^t\in R^{d_h\times d_h} WQt∈Rdh×dk,WKt∈Rdh×dk,Wt∈Rdh×dh 是可学习的权重矩阵, b t ∈ R d h b^t\in R^{d_h} bt∈Rdh 是偏置向量, d k d_k dk 是注意机制的隐藏维度。为了计算 h i t h_i^t hit,该模型通过注意系数 a i j t a_{ij}^t aijt 将其一阶领域(包括其自身)的隐藏状态线性组合,然后使用非线性激活函数 f f f。每个节点的最终输出是所有头的输出的平均值。此外,上述计算过程将在 l l l 层的 SGAT 中迭代 l l l 次。
(2)自监督
我们提出了一种旨在引导注意力与基于依赖关系的解析树中节点对间是否存在边保持一致的 SGAT。其中由基于依赖关系的解析树构成的邻接矩阵 A ∈ R N × N A\in R^{N\times N} A∈RN×N 称为依赖矩阵。若节点 i i i 和节点 j j j 有边,那么 A i j A_{ij} Aij 和 A j i A_{ji} Aji 将会被设为 1,否则设为 0。此外,我们规定 A i i = 1 A_{ii}=1 Aii=1。注意力矩阵 A ~ \widetilde{A} A 计算方法如下: A ~ = sigmoid ( W Q X × ( W K X ) T d k ) (4) \widetilde{A}=\text{sigmoid}\Big(\frac{W_QX\times(W_KX)^T}{\sqrt{d_k}}\Big)\tag{4} A =sigmoid(dkWQX×(WKX)T)(4)与公式(1)相比,我们使用 sigmoid \text{sigmoid} sigmoid 函数代替 softmax \text{softmax} softmax 映射 A ~ i j \widetilde{A}_{ij} A ij 来表示节点 i i i 和节点 j j j 有依赖边的概率。训练目标是最小化注意矩阵和依赖矩阵的损失值。值得注意的是,我们利用多头注意机制来生成多个注意矩阵,但每层只会选择一个。因为依赖边可以分为存在和不存在,所以链接预测实际上是一个二分类任务。我们将优化目标定义为二元交叉熵损失: L s = 1 N × N ∑ i = 1 N ∑ j = 1 N ( − A i j ⋅ log A ~ i j + ( 1 − A i j ) log ( 1 − log A ~ i j ) ) (5) L_s=\frac{1}{N\times N}\sum_{i=1}^N\sum_{j=1}^N\Big(-A_{ij}·\log\widetilde{A}_{ij}+(1-A_{ij})\log(1-\log\widetilde{A}_{ij})\Big)\tag{5} Ls=N×N1i=1∑Nj=1∑N(−Aij⋅logA ij+(1−Aij)log(1−logA ij))(5)
2.3 Gumbel Tree-GRU 层
潜在树学习通过自动学习适合特定任务的结构特征,在各种NLP任务中取得了巨大成功。利用工具生成的依赖句法结构不仅噪音大,而且不适合下游任务。因此,我们引入了如图所示的 Gumbel Tree-GRU,其传播过程可以看作是基于选区的解析树,比基于依赖关系的解析树更适合 BioRE。
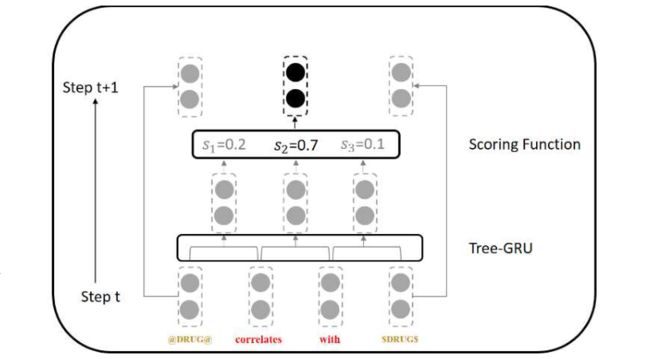
在第 t t t 步,通过共享 Tree-GRU 单元,将相邻单词或短语的两个特征向量转换为一个候选向量。然后候选向量将由评分函数访问。在第 t + 1 t+1 t+1 步,选择具有最大概率的候选向量,并直接从上一步复制其余向量。因此,在 n − 1 n-1 n−1 个步骤后,只有一个向量 h s h_s hs 被保留,我们使用该向量代表句子信息。
(1)Tree-GRU
我们使用一个共享权重的树形结构 GRU 单元来将相邻特征向量 h j h_j hj 和 h j + 1 h_{j+1} hj+1 合成一个新的向量 h h h: i = σ ( W i h j + U i h j + 1 + b i ) (6) i=\sigma(W_ih_j+U_ih_{j+1}+b_i)\tag{6} i=σ(Wihj+Uihj+1+bi)(6) f = σ ( W f h j + U f h j + 1 + b f ) (7) f=\sigma(W_fh_j+U_fh_{j+1}+b_f)\tag{7} f=σ(Wfhj+Ufhj+1+bf)(7) r = σ ( W r h j + U r h j + 1 + b r ) (8) r=\sigma(W_rh_j+U_rh_{j+1}+b_r)\tag{8} r=σ(Wrhj+Urhj+1+br)(8) h ~ = tanh ( W h ( r ⊙ h j ) + U h ( r ⊙ h j + 1 ) + b h ) (9) \widetilde{h}=\text{tanh}(W_h(r⊙h_j)+U_h(r⊙h_{j+1})+b_h)\tag{9} h =tanh(Wh(r⊙hj)+Uh(r⊙hj+1)+bh)(9) h = i ⊙ h ~ + f ⊙ ( h j + h j + 1 ) (10) h=i⊙\widetilde{h}+f⊙(h_j+h_{j+1})\tag{10} h=i⊙h +f⊙(hj+hj+1)(10)其中 W i ∈ R d h × d h , U i ∈ R d h × d h , W f ∈ R d h × d h , U f ∈ R d h × d h , W r ∈ R d h × d h , U r ∈ R d h × d h , W h ∈ R d h × d h , U h ∈ R d h × d h W_i\in R^{d_h\times d_h},U_i\in R^{d_h\times d_h},W_f\in R^{d_h\times d_h},U_f\in R^{d_h\times d_h},W_r\in R^{d_h\times d_h},U_r\in R^{d_h\times d_h},W_h\in R^{d_h\times d_h},U_h\in R^{d_h\times d_h} Wi∈Rdh×dh,Ui∈Rdh×dh,Wf∈Rdh×dh,Uf∈Rdh×dh,Wr∈Rdh×dh,Ur∈Rdh×dh,Wh∈Rdh×dh,Uh∈Rdh×dh 都是待学习的权重矩阵, b i ∈ R d h , b f ∈ R d h , b r ∈ R d h , b h ∈ R d h b_i\in R^{d_h},b_f\in R^{d_h},b_r\in R^{d_h},b_h\in R^{d_h} bi∈Rdh,bf∈Rdh,br∈Rdh,bh∈Rdh 都是偏置向量, ⊙ ⊙ ⊙ 元素态乘积, σ \sigma σ 是 sigmoid \text{sigmoid} sigmoid 激活函数。
(2)评分函数
评分函数用于评估每个步骤中的所有候选特征向量。在第 t t t 步,由公式(10)计算的候选向量集被表示为 ( c 1 , c 2 , ⋯ , c N − t ) (c_1,c_2,\cdots,c_{N-t}) (c1,c2,⋯,cN−t),其中 c i ∈ R d h c_i\in R^{d_h} ci∈Rdh 是第 i i i 个候选特征向量。第 i i i 个候选向量未归一化的分数计算公式如下: π i = W π tanh ( V π c i ) (11) \pi_i=W_{\pi}\text{tanh}(V_{\pi}c_i)\tag{11} πi=Wπtanh(Vπci)(11)其中 W π ∈ R 1 × d h , V π ∈ R d h × d h W_{\pi}\in R^{1\times d_h},V_{\pi}\in R^{d_h\times d_h} Wπ∈R1×dh,Vπ∈Rdh×dh 是可学习的权重矩阵。然后用 Gumbel-Softmax 进行归一化处理: y i = e log ( π i ) + g i τ ∑ j = 1 N − t e log ( π i ) + g i τ (12) y_i=\frac{e^{\frac{\log(\pi_i)+g_i}{\tau}}}{\sum_{j=1}^{N-t}e^{\frac{\log(\pi_i)+g_i}{\tau}}}\tag{12} yi=∑j=1N−teτlog(πi)+gieτlog(πi)+gi(12)其中 τ \tau τ 是初始值为 1 的可学习的温度系数, g i ∈ ( 0 , 1 ) g_i\in (0,1) gi∈(0,1) 是一个采样噪声,计算公式如下: g i = − log ( − log ( u i ) ) (13) g_i=-\log(-\log(u_i))\tag{13} gi=−log(−log(ui))(13)其中 u i ∈ ( 0 , 1 ) u_i\in (0,1) ui∈(0,1)。具有最高的 y y y 值的候选特征向量 c c c 将会参与第 t + 1 t+1 t+1 步的操作。
2.4 知识融合层
我们从上一个自监督图注意层的输出抽取实体对的特征,用 h h e a d h_{head} hhead 和 h t a i l h_{tail} htail 表示。并用如下公式拼接起来: h f i n a l = [ h h e a d ; h s ; h t a i l ] (14) h_{final}=[h_{head};h_{s};h_{tail}]\tag{14} hfinal=[hhead;hs;htail](14)将 h f i n a l h_{final} hfinal 作为全连接层的输入,利用 softmax \text{softmax} softmax 函数进行归一化处理: P ( r ∣ h f i n a l ) = softmax ( W f h f i n a l + b f ) (15) P(r|h_{final})=\text{softmax}(W_fh_{final}+b_f)\tag{15} P(r∣hfinal)=softmax(Wfhfinal+bf)(15)其中 W f W_f Wf 是权重矩阵, b f b_f bf 是偏置向量, r r r 是关系类型。由于我们已经引入了自监督任务,因此最终损失函数如下: L = L r + λ s ⋅ L s (16) L=L_r+\lambda_s·L_s\tag{16} L=Lr+λs⋅Ls(16)其中 L r L_r Lr 是关系分类的交叉熵损失, L s L_s Ls 是自监督任务的损失, λ s \lambda_s λs 是权重系数。
3. Experiments
3.1 Datasets and Experimental Settings
为了评估我们的 SGAT 在 BioRE 任务中的性能,我们对 DDIExtraction 2013 数据集和 ChemProt 数据集进行了实验。根据 Peng 等人的操作对语料库进行预处理,DDIExtraction 2013 和 ChemProt 任务是多分类问题,我们使用微平均精度、召回率和F1值作为评价指标。
我们使用 BioBERT 对 PubMed摘要 和 PMC文章 进行预训练,以生成初始词嵌入。Stanford解析器用于生成句子的依存句法信息。所有隐藏层大小都设置为300。采用 Adam 优化器,learning_rate=2e-5,L2权重衰减为0.01,dropout=0.5,mini_batch_size=16,max_seq=256,头数为2,自监督图形注意层数为2, λ s \lambda_s λs=0.3。
3.2 Performance Comparision
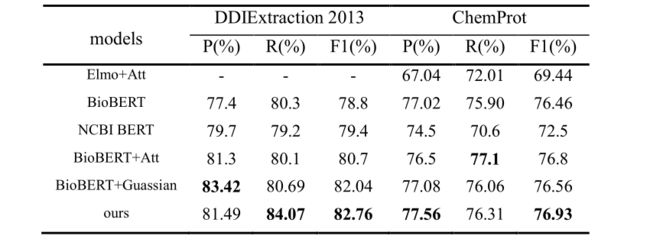
Elmo+Att 使用 Elmo 和实体注意机制,然而,性能并不令人满意,这表明使用基于 Elmo-based 的方法很难有效地执行 BioRE。BioBERT 是 BERT 在PubMed的生物医学文本进一步预训练所得。NCBI BERT 使用 PubMed 摘要和 clinical notes(MIMIC-III)进行训练,然后针对不同的生物医学任务进行微调。BioBERT+Att 使用 BioBERT 提取单词特征,并为BioBERT的每个输出指定权重并应用注意机制来组合序列。BioBERT+Guassian 使用高斯分布来聚集句子信息,并集成外部知识以提高提取性能。
3.3 Ablation Study
为了验证 SGAT 的有效性,我们对 DDIExtraction 2013 数据集进行了消融研究。在实验中,–SS 表示去掉自我监督部分,删除后F1分数下降了0.9%,这表明自监督任务可以通过这种句法信息的引导提高 GAT 的能力。–SGAT 表示删除了具有自我监督的 GAT,删除后F1分数下降了1.59%,表明GAT也可以学习有效特征。此外,–GT 表示不使用 Gumbel Tree GRU 生成句子表示,而只是平均每个句子的所有单词表示。结果表明,Gumbel Tree GRU更适合 BioRE。总的来说,每个模块都有助于最终的改进,而 SGAT 带来了最大的改进,这证明了我们提出的模型在 BioRE 任务中的有效性。