Categorical Reparameterization with Gumbel-Softmax

下面写如何从多项分布里采样

从Gumbel(0;1)分布里采样方法

The Gumbel(0; 1) distribution can be sampled using inverse transform sampling。
fristly, drawing u from Uniform(0; 1) and then computing：

g = -log(-log(u)).  

g就代表从gumbel里采样到的点

OneHotCategorical

The categorical distribution is parameterized by the log-probabilities of a set of classes. The difference between OneHotCategorical and Categorical distributions is that OneHotCategorical is a discrete distribution over one-hot bit vectors whereas Categorical is a discrete distribution over positive integers.

也就是说：

• OneHotCategorical 是一个离散分布p（x），只是他的变量x是一个one-hot向量。
• Categorical distributions也是一个离散分布p(y),只是y是一个标量。

从Categorical distributions里采样得到一个OneHotCategorical采样点的过程：

The Gumbel-Max trick provides a simple and efficient way to draw samples z from a categorical distribution with class probabilities π ， π 就是多项分布的分布函数:

上式表示从gumbel分布里依次采样N个点，第i个采样点用 gi 表示(N表示categorical 分布的可选值个数),。对每个采样点计算 gi+logπi , 然后求出N个采样计算值里最大的那个，比如第j个采样计算值是最大的，则将长度为N的z向量里第j个元素的值设为1，其他的element都设置为0，得到一个one-hot 向量。这个one-hot向量就代表这个categorical 分布的一个采样点。也就是说要得到一个离散分布的采样点，需要从gumbel里采样N个点。

在https://gist.github.com/gngdb/ef1999ce3a8e0c5cc2ed35f488e19748 这篇文章里用图标的形式证明这种方法的正确性。

RelaxedOneHotCategorical

The RelaxedOneHotCategorical is a distribution over random probability vectors, vectors of positive real values that sum to one, which continuously approximates a OneHotCategorical. The degree of approximation is controlled by a temperature: as the temperature goes to 0 the RelaxedOneHotCategorical becomes discrete with a distribution described by the logits or probs parameters。

也就是说RelaxedOneHotCategorical是一个连续的多变量分布p(x,y,z)，但是x+y+z=1. 他是对OneHotCategorical离散分布的一个连续近似。近似的程度由一个temperature 控制。

Creates a continuous distribution, which approximates a 3-class one-hot categorical distribution. Because the temperature is very low, samples from this distribution are almost discrete, with one component almost 1 and the others nearly 0. The 2nd class is the most likely to be the largest component in samples drawn from this distribution.

创建一个连续的分布来近似一个具有三个类别的one-hot categorical distribution。当temp很小时，他的采样结果就是一个one-hot向量，即一个采样结果向量里只有一个值为1，其他值为0。

temperature = 1e-5
#logits是没归一化的向量，代表要近似的one-hot categorical distribution
logits = [-2, 2, 0]
当temperature很小时，从dist 分布的采样结果将近似于一个one-hot向量
dist = RelaxedOneHotCategorical(temperature, logits=logits)

在论文里写到
We use the softmax function as a continuous, differentiable approximation to argmax, and generate K-dimensional sample vectors y：

即用连续且可微的softmax来近似 argmax，来生成k维的采样向量，这里k和上面的N是相同的，表示categorical 分布的可选值个数。这种方法得到的一个采样(向量)里，每个元素 yi 可以同时不为0。

生成这个采样向量的概率为：

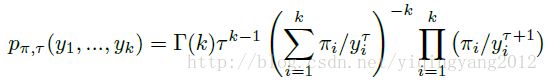
其中 y1+y2+...+yk=1 。这个 p 就是RelaxedOneHotCategorical的概率密度分布。

ST-Gumbel-softmax

参考 https://gabrielhuang.gitbooks.io/machine-learning/reparametrization-trick.html

For non-zero temperatures, a Gumbel-softmax variable x does not exactly follow Cat(π). but If we replace x with its argmax in the forward pass , then we get a one-hot variable following exactly Cat(πϕ). However, in order to backpropagate the gradient, we can still keep the original continuous x in the backward pass.

This is called Straight-Through-Gumbel-softmax in Jang’s paper, and builds on ideas from Bengio, Leonard, Courville (2013) - Estimating or Propagating Gradients

implement

下面是一个用gumbel做无监督生成的代码。注意：这里y的每一维yi是离散的category 分布 p(yi) ，且y的先验分布为均匀分布；而在base VEA里y是一个多维高斯分布，且认为y的先验分布是多维正态高斯分布~N(0,1). 这里0是一个向量，代表均值，1是一个协方差矩阵(对角线上的元素全为1，其他元素全为0).
代码来自：https://github.com/ericjang/gumbel-softmax/blob/master/Categorical%20VAE.ipynb

def sample_gumbel(shape, eps=1e-20): 
  """Sample from Gumbel(0, 1)"""
  U = tf.random_uniform(shape,minval=0,maxval=1)
  return -tf.log(-tf.log(U + eps) + eps)

def gumbel_softmax_sample(logits, temperature): 
  """ Draw a sample from the Gumbel-Softmax distribution"""
  y = logits + sample_gumbel(tf.shape(logits))
  return tf.nn.softmax( y / temperature)

def gumbel_softmax(logits, temperature, hard=False):
  """Sample from the Gumbel-Softmax distribution and optionally discretize.
  Args:
    logits: [batch_size, n_class] unnormalized log-probs
    temperature: non-negative scalar
    hard: if True, take argmax, but differentiate w.r.t. soft sample y
  Returns:
    [batch_size, n_class] sample from the Gumbel-Softmax distribution.
    If hard=True, then the returned sample will be one-hot, otherwise it will
    be a probabilitiy distribution that sums to 1 across classes
  """
  y = gumbel_softmax_sample(logits, temperature)
  if hard:
    k = tf.shape(logits)[-1]
    #y_hard = tf.cast(tf.one_hot(tf.argmax(y,1),k), y.dtype)
    y_hard = tf.cast(tf.equal(y,tf.reduce_max(y,1,keep_dims=True)),y.dtype)
    y = tf.stop_gradient(y_hard - y) + y

K=10 # number of classes #即每个类有多少个可选值
N=30 # number of categorical distributions 即总共有多少个类

# input image x (shape=(batch_size,784))
x = tf.placeholder(tf.float32,[None,784])
#下面相当于叠加了两个全连接层，第一个的输出节点数为512，第二个的输出节点数为256
net = slim.stack(x,slim.fully_connected,[512,256])

# unnormalized logits for N separate K-categorical distributions
#得到的logits_y的shape=(batch_size*N,K)
logits_y = tf.reshape(slim.fully_connected(net,K*N,activation_fn=None),[-1,K])
q_y = tf.nn.softmax(logits_y)
log_q_y = tf.log(q_y+1e-20)

# temperature
tau = tf.Variable(5.0,name="temperature")
#采样
# set hard=True for ST Gumbel-Softmax。采样结束后将(batch_size*N,K)变为(batch_size,N,K))
#由于这里将hard设置为false，则最后一维不是one-hot形式
y = tf.reshape(gumbel_softmax(logits_y,tau,hard=False),[-1,N,K])

# generative model p(x|y)))
#flatten：将输入扁平化但保留batch_size不变，后面的维度变成一维，所以net的shape为[batch_size,512]
net = slim.stack(slim.flatten(y),slim.fully_connected,[256,512])
logits_x = slim.fully_connected(net,784,activation_fn=None)
#得到的(shape=(batch_size,784))在Bernoulli里会对每个element计算一个sigmoid(logits)，这样每个
#element的值都在(0,1)之间
p_x = Bernoulli(logits=logits_x)

# loss and train ops.

#KLloss
#求期望时认为y的各维是相互独立的，所以下面相当于先各维独立求期望(在第2维上)，再
#将各维的期望相加(第1维上)
kl_tmp = tf.reshape(q_y*(log_q_y-tf.log(1.0/K)),[-1,N,K])
KL = tf.reduce_sum(kl_tmp,[1,2])

#reconstruction error
reco = tf.reduce_sum(p_x.log_prob(x),1)

#total loss
elbo=reco  - KL

loss=tf.reduce_mean(-elbo)
lr=tf.constant(0.001)
train_op=tf.train.AdamOptimizer(learning_rate=lr).minimize(loss,var_list=slim.get_model_variables())
init_op=tf.initialize_all_variables()

在半监督应用里，求KL和信息熵H

对于unlabled，datas，当引入一个隐含离散变量y和一个隐含连续向量z时，认为
q(y,z|x)=q(y|x)∗q(z|x,y)
p(x,y,z)=p(x|y,z)∗p(z)p(y)
loss函数的计算公式如下

论文里， H=Σyq(y|x)logq(y|x) ,但在下面的代码里将 Σyq(y|x)logq(y) 也放在H里一起计算了。

            with tf.name_scope('Unlabeled'):
                z_mu = unlabel['z_mu']
                z_lv = unlabel['z_lv']
                loss['KL(z_u)'] = tf.reduce_mean(
                    GaussianKLD(
                        z_mu, z_lv,
                        tf.zeros_like(z_mu), tf.zeros_like(z_lv)))

                loss['log p(x_u)'] = tf.reduce_mean(
                    tf.reduce_sum(
                        tf.nn.sigmoid_cross_entropy_with_logits(
                            logits=slim.flatten(unlabel['xh_sig_logit']),
                            targets=slim.flatten(x_u)),
                        1))
                #[batch, class]p(y)先验分布
                y_prior = tf.ones_like(unlabel['y_sample']) / self.arch['y_dim']
                )
                #unlabel['y_pred']代表infer到的q(y)分布
                loss['H(y)'] = tf.reduce_mean(                
                    tf.reduce_sum(
                        tf.mul(
                            unlabel['y_pred'],
                            tf.log(unlabel['y_pred'] + EPS) - tf.log(y_prior)),
                        -1))

KL和reconstruction error在y维度上的积分都是用采样估计的方法，KL在z维度上的积分采用解析的方法直接计算。计算H时，由于 p(y) 和 q(y|x )里都不包含所以公式里第二个积分符号可以去掉，只剩下第一个积分符号。

互信息loss

互信息的引入可以参考 https://serhii-havrylov.github.io/blog/mutual_info
计算生成的x和z的互信息 I(x,z) ,互信息越大表示两者相关性越强，如果I=0，则认为两者完全不相干。引入互信息是使生成的x和z要尽量相关，即在generator里生成x时要多考虑z，否则就是个普通的无条件language model。
计算互信息时，需要用到一些trick，可以参考论文 Challenges with Variational Autoencoders for Text。

积分不能直接求解，所以只能用采样的方法.

• qMI(z|x) ：是一个高斯分布，其均值和方差为generator的输出再输入到encoder后求得。
• z：将最初x输入到encoder得到VAE里的高斯分布 q(z|x) ,然后采样得到。
• p(z) 为标准正太分布。

上式用估计的方法求解其实就是求两个高斯分布在z处的log似然概率之差。

    #z: 从encoder得到的q(z)分布里采样到的值
    '''
    z_mean和z_logvar是q_mi(z|x)高斯分布的均值和方差。q_mi(z|x)的输入x是从generator
    里得到的logis串联上lable的embeding(在sentiment里表示positive or negtive)和mask(表示每个step是否真的有数据)。q_mi(z|x)用一个encoder实现。
    '''
    #两个高斯分布的互信息，第一个高斯分布以z_mean和z_logvar为参数，第二个高斯是标准正态分布N(0,1)
    def mutinfo_loss(self, z, z_mean, z_logvar):
        '''Mutual information loss. We want to maximize the likelihood of z in the
           Gaussian represented by z_mean, z_logvar.''' 
        z = tf.stop_gradient(z)
        z_var = tf.exp(z_logvar) + 1e-8 
        z_logvar = tf.log(z_var)  # adjust for epsilon

        z_sq = tf.square(z)
        z_epsilon = tf.square(z - z_mean)

        return 0.5 * tf.reduce_sum(z_logvar + (z_epsilon / z_var) - z_sq, 1)