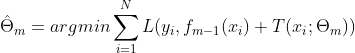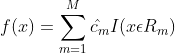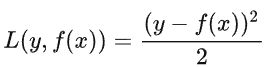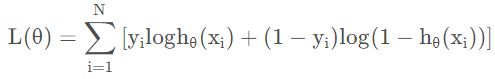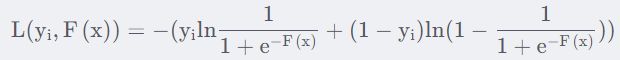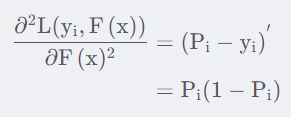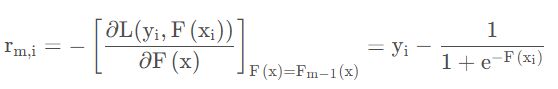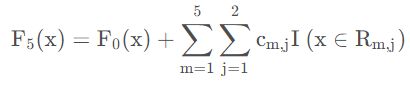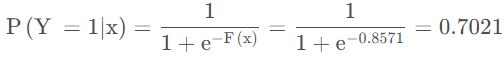GBDT算法详解&算法实例（分类算法）
哈喽小天才们~今天和大家来唠一唠GBDT，对于怕麻烦的我，写这篇文章可是下了很大的决心，因为公式实在是太多啦o(╥﹏╥)o
之前写了几篇关于机器学习的代码实操，原理部分基本上都是几行一大段就简述了，今天我打算好好写一写GBDT的算法原理，毕竟是集成算法的代表选手，还是要尊重一下的
本人之前对GBDT的算法并没有很深入的推算过，所以借着这个机会，整理一下我的学习笔记，把之前一带而过的公式推导手推了一遍，同时也希望这篇文章能帮到还在GBDT算法原理徘徊的姐妹们，别犹豫了，拿起纸笔加入我吧hhhh
一、提升树模型
提升方法实际采用加法模型（即基函数的线性组合）与前向分步算法。以决策树为基函数的提升方法称为提升树（boosting tree）。
1、提升树算法
提升树算法采用前向分步算法．首先确定初始提升树 
，第 m 歩的模 型是
其中，
为当前模型，通过经验风险极小化确定下一棵决策树的参数
，
由于树的线性组合可以很好地拟合训练数据，即使数据中的输入与输出之间的关系很复杂也是如此，所以提升树是一个高功能的学习算法。
提升树学习算法之间的区别主要在于使用的损失函数不同，包括用平方误差损失函数的回归问题，用指数损失函数的分类问题，以及用一般损失函数的一般决策问题。对于二类分类问题，提升树算法只需将AdaBoost 算法中的基分类器限制为二分类树即可，这时提升树算法是 AdaBoost 算法的特殊情况。
同时有一点需要注意，在boosting算法家族中，除了adaboost会使用分类决策树为基学习器以外，其余算法如GBDT、XGBoost等，都是建立在CART回归树的基础上，换句话说就是不管处理分类问题还是回归问题，我们的基学习器都是CRAT回归树，为什么这样做，原因会在后面解释。
2、CART回归树
既然GBDT的基学习器是cart回归树，按我们首先来回顾一下cart回归树算法：
输入：训练数据集 D
输出：回归树
在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树：
（1）选择最优切分变量 j 与切分点 s ，求解
![\underset{j,s}{min}[\underset{c_{1}}{min}\sum_{x_{i}\epsilon R_{1}(j,s)}^{}(y_{i}-c_{1})^{2}+\underset{c_{2}}{min}\sum_{x_{i}\epsilon R_{2}(j,s)}^{}(y_{i}-c_{2})^{2}]](http://img.e-com-net.com/image/info8/6fddacc4f33a4836b7e28fe4b35c8081.gif){kind=small}
遍历变量 j ，对固定的切分变量 j 扫描切分点 s ，选择使上式达到最小值的对(j, s)
（2）用选定的对(j, s)划分区域并决定相应的输出值：
（3）继续对两个子区域调用步骤 (1)，(2)，直至满足停止条件
（4）将输入空间划分为 M 个区域 
，生成决策树：
二、GDBT算法原理
1、GBDT为什么使用负梯度
在我们刚接触boosting集成算法时，就应该了解到它的思想是一个不断优化的过程，每一棵树都要去弥补前一棵树与真实值之间的差距，也就是残差。
比如现在要预测收入，真实值为1000，第一棵树拟合值为700，那第二棵树的目标就是把700和1000之间的距离补上，这时第二棵树的拟合目标就变为300而不是1000，这种思想就是在拟合残差达到不断优化的目的。
这种做法十分有效，但也具有一定的局限性，当我们的损失函数为平方损失和指数损失函数时，按照拟合残差的原理，每一步优化是很简单的，但是对于一般的损失函数而言，比如逻辑回归使用的对数损失函数而言，优化往往没有那么容易。针对这一问题，Freidman 提出了梯度提升（gradient boosting）算法。这是利用最速下降法的近似方法，其关键是利用损失函数的负梯度在当前模型的值
作为回归问题提升树算法中的残差的近似值，拟合一个回归树。也就是说残差只是损失函数负梯度的一种特例，而采用负梯度更加通用，可以使用不同的损失函数，对于这点，下面会给出证明。
这也就可以解释为何对于分类问题来说，GBDT的基函数也是回归树的原因了，因为我们需要计算负梯度，需要求偏导，这时分类树是不能满足这种需求的。
2、为何负梯度可以替代残差
其实很多人对于为什么使用负梯度来代替残差得原因总是模糊的，我也是在不断查阅文章、手推公式后才逐渐清晰。首先我们先从最简单的损失函数入手，当我们的损失函数为平方损失函数时：
这个也就是我们平时说的均方误差MSE，它的负梯度就是对MSE求偏导为：
这不就是残差吗姐妹们，也就是说，当损失函数采用MSE时，残差就等价于它的负梯度。
上面举的例子是比较特殊的情况，那么对于一般的损失函数来说，为何拟合损失函数的负梯度就可以不断达到优化的目的呢？（此处参考博文： GBDT理解难点------拟合负梯度 - 知乎 (zhihu.com)）下面是一段硬核推导，希望姐妹们拿着纸笔耐心看完：
首先从泰勒公式入手，因为GBDT是个加法模型，而泰勒展开后公式也是相加的形式，同时也包含导数：
普通泰勒展开
结合加法模型后
同理我们对损失函数进行泰勒展开：
出现负梯度了昂姐妹们~看到希望了
由于GBDT是加法模型，假设我们现在学习第K棵树，则：
把（2）带入（1）得：
化简移项：
因为我们在拟合第K颗树时，K-1棵树已经定下来了，所以我们希望第K颗树的损失函数尽可能小的话，也就是约等号左边的式子要尽可能小，等价于右边的式子也要尽可能小：
众所周知，沿着负梯度方向，损失函数是下降的最快的，因此GBDT优化过程中拟合负梯度是合理的，第k棵树本质就是在拟合当前损失函数的负梯度。
3、GBDT二分类算法
3.1 逻辑回归的对数损失函数
逻辑回归的预测函数：
逻辑回归的对数损失函数：
逻辑回归的对数似然函数：
3.2 GBDT二分类算法过程
（1）初始化弱学习器：
（2）建立M颗用于分类的回归树
a）计算第m棵树对应的响应值，即第m棵树需要拟合的负梯度：
b）对于划分到同一边的样本，计算最佳拟合值：
对于最佳拟合值
的手推公式如下（此处参考博文： 深入理解GBDT二分类算法_Microstrong0305的博客-CSDN博客_gbdt分类）：
理论上，对于生成的决策树，计算各个叶子节点的最佳残差拟合值为：
由于上式没有闭式解（closed form solution），所以一般使用近似值代替
假设有一个样本：
求一阶导：
求二阶导：
对于损失函数进行泰勒二阶展开：
仔细观察上式，其实就是关于c的二元一次方程，也就是当
，损失函数取得最值，即：
d）更新
：
（3）组合每轮学习器结果，组成强学习器：
3.3 GBDT算法实例演示
（1）数据集情况
实例参考此篇博文： GBDT算法原理以及实例理解_Freeman_zxp的博客-CSDN博客_gbdt
训练数据集：4个样本，两列特征分别为年龄和体重，label为身高是否大于1.5米，具体数据情况如下表：
| 编号 | 年龄 | 体重 | label |
|---|---|---|---|
| 0 | 5 | 20 | 0 |
| 1 | 7 | 30 | 0 |
| 2 | 21 | 70 | 1 |
| 3 | 30 | 60 | 1 |
测试数据集：1个样本，需要预测其身高是否大于1.5米，具体数据情况如下：
| 编号 | 年龄 | 体重 | label |
|---|---|---|---|
| 0 | 25 | 65 | ？ |
（2）模型训练
GBDT参数设置：
基学习器个数 n_trees = 5
树深 max_depth = 3
①初始化弱学习器：
对于逻辑回归算法来说，初始化弱学习器定义为：样本属于1的概率 / 样本属于0的概率，再取个log，这里4个样本的初始值均为0
②建立M颗用于分类的回归树
由于我们在模型训练开始前设置了基学习器的个数为5，所以M=5，也就是一共迭代5轮，生成5颗CART树
首先计算负梯度，决定第一棵树的拟合值目标：
依次把真实label—y和初始化弱学习器值—F(x)带入上式，即可求得每一个样本的负梯度值：
| 编号 | label |  |
负梯度 |
|---|---|---|---|
| 0 | 0 | 0 | -0.5 |
| 1 | 0 | 0 | -0.5 |
| 2 | 1 | 0 | 0.5 |
| 3 | 1 | 0 | 0.5 |
负梯度作为第一棵树的拟合目标：
| 编号 | 年龄 | 体重 | 负梯度 |
|---|---|---|---|
| 0 | 5 | 20 | -0.5 |
| 1 | 7 | 30 | -0.5 |
| 2 | 21 | 70 | 0.5 |
| 3 | 30 | 60 | 0.5 |
接着寻找回归树的最佳划分节点，遍历每个特征的每个取值。从年龄5开始，到体重70结束，共有8中划分方式，依次计算划分后的平方损失，
为左半部分的平方损失，
为右半部分的平方损失，找到使平方损失和 
最小的那个划分节点，即为最佳划分节点。
举例：以年龄7为划分点，将小于7的划分为到左节点，大于等于7的划分为右节点，左节点包括样本
，样本均值为-0.5，
，右节点包括样本
，样本均值为 (-0.5+0.5+0.5) / 3 = 1/6 ,![SE_{R}=[(-0.5-1/6)^{2}+(0.5-1/6)^{2}+(0.5-1/6)^{2}]/3=0.667](http://img.e-com-net.com/image/info8/3ff42612fc58461192f0747e3d5a6076.gif){kind=small}
，
所有可能的划分情况如下表所示：
| 划分点 | <划分点的样本 | >=划分点的样本 | |
|
 |
|---|---|---|---|---|---|
| 年龄5 | / | 0,1,2,3 | 0 | 1 | 1 |
| 年龄7 | 0 | 1,2,3 | 0 | 0.667 | 0.667 |
| 年龄21 | 0,1 | 2,3 | 0 | 0 | 0 |
| 年龄30 | 0,1,2 | 3 | 0.667 | 0 | 0.667 |
| 体重20 | / | 0,1,2,3 | 0 | 1 | 1 |
| 体重30 | 0 | 1,2,3 | 0 | 0.667 | 0.667 |
| 体重60 | 0,1 | 2,3 | 0 | 0 | 0 |
| 体重70 | 0,1,3 | 2 | 0.667 | 0 | 0.667 |
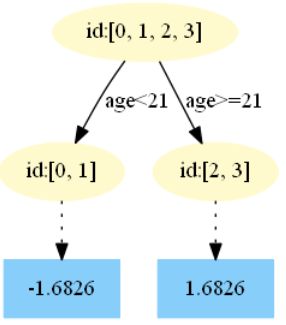
如上表所示，总平方损失最小值为0，共有两个划分点分别为：年龄21和体重60，随机选取一个作为划分点即可，这里选年龄21为划分点，第一棵树的第一次分裂如下：
因为我们在开始训练前设置树深为3，现在有两层，应该继续分类一次，但是目前我们的左右节点都只包含一种label，样本0和样本1的label都是0，样本2和样本3的label都是1，这时已经没必要再往下分了，所以我们第一课树就训练完毕。因为是回归树，所以需要计算左右节点的拟合值：
举例计算一下：左节点拟合值
同理右节点
则第一棵树为：
更新学习器：
举例：对于第一个样本来说
依次算出四个样本的
，在通过
计算新一轮负梯度用于拟合第二棵树，依次循环以上步骤，直到5棵树训练完毕，结束循环。
最后展示一下5颗树的分裂情况：
第一棵树
第二棵树
第三棵树
第四棵树
第五棵树
③得到最终强学习器：
（3）模型预测
在中，测试样本的年龄为25，大于划分节点21岁，所以被预测为2
在
中，测试样本的年龄为25，大于划分节点21岁，所以被预测为1.8187
在
中，测试样本的年龄为25，大于划分节点21岁，所以被预测为1.6826
在
中，测试样本的年龄为25，大于划分节点21岁，所以被预测为1.5769
在
中，测试样本的年龄为25，大于划分节点21岁，所以被预测为1.4927
最终预测结果为：
本人才疏学浅，若有理解有误的地方，还请各路大佬批评指正♡♡♡
ok！感恩的心~
四、Reference
[1]《统计学习方法》，李航著
[2] 深入理解GBDT二分类算法_Microstrong0305的博客-CSDN博客_gbdt分类
[3] GBDT理解难点------拟合负梯度 - 知乎 (zhihu.com)
[4] GBDT梯度提升树算法原理 - 知乎 (zhihu.com)
[5] GBDT算法原理以及实例理解_Freeman_zxp的博客-CSDN博客_gbdt